9. 如图,小明将一张正方形纸片剪去一个宽为3 cm的长条后,再从剩下的长方形纸片上剪去一个宽为4 cm的长条.若两次剪下的长条面积正好相等,则剪下的长条的面积之和为
72
$cm^{2}$.答案：【解析】：本题考查一元一次方程的实际应用。
设正方形的边长是 x cm，
根据题意，第一次剪下的长条的面积为$ 3x cm^2，$
第二次剪下的长条的面积为$ 4(x - 3) cm^2。$
因为两次剪下的长条面积相等，所以有
3x = 4(x - 3)，
展开得：
3x = 4x - 12，
移项并化简得：
x = 12。
第一次剪下的长条的面积为：
$3 × 12 = 36 （cm^2），$
因为两次剪下的长条面积相等，所以两次剪下的长条的面积之和为：
$36 × 2 = 72（ cm^2）。$
【答案】：72。
设正方形的边长是 x cm，
根据题意，第一次剪下的长条的面积为$ 3x cm^2，$
第二次剪下的长条的面积为$ 4(x - 3) cm^2。$
因为两次剪下的长条面积相等，所以有
3x = 4(x - 3)，
展开得：
3x = 4x - 12，
移项并化简得：
x = 12。
第一次剪下的长条的面积为：
$3 × 12 = 36 （cm^2），$
因为两次剪下的长条面积相等，所以两次剪下的长条的面积之和为：
$36 × 2 = 72（ cm^2）。$
【答案】：72。
10. (2025·江苏常州期末)如图,图①是由6块完全相同的三角形地砖铺成,图②是由10块完全相同的三角形地砖铺成,图③是由14块完全相同的三角形地砖铺成,….按图中所示规律,若图n所需三角形地砖的块数为482,则$n= $
120
.答案：【解析】：
本题可先通过分析图中地砖数量的规律，得出图$n$所需三角形地砖块数的表达式，再根据已知条件列出方程求解$n$的值。
观察图形可知：
图①是由$6$块完全相同的三角形地砖铺成，可写成$6 = 4×1 + 2$；
图②是由$10$块完全相同的三角形地砖铺成，可写成$10 = 4×2 + 2$；
图③是由$14$块完全相同的三角形地砖铺成，可写成$14 = 4×3 + 2$。
以此类推，可得图$n$所需三角形地砖的块数为$4n + 2$。
已知图$n$所需三角形地砖的块数为$482$，则可列出方程$4n + 2 = 482$，接下来求解该方程：
首先，方程两边同时减去$2$可得：$4n + 2 - 2 = 482 - 2$，即$4n = 480$。
然后，方程两边同时除以$4$可得：$4n÷4 = 480÷4$，解得$n = 120$。
【答案】：
$120$
本题可先通过分析图中地砖数量的规律，得出图$n$所需三角形地砖块数的表达式，再根据已知条件列出方程求解$n$的值。
观察图形可知：
图①是由$6$块完全相同的三角形地砖铺成，可写成$6 = 4×1 + 2$；
图②是由$10$块完全相同的三角形地砖铺成，可写成$10 = 4×2 + 2$；
图③是由$14$块完全相同的三角形地砖铺成，可写成$14 = 4×3 + 2$。
以此类推，可得图$n$所需三角形地砖的块数为$4n + 2$。
已知图$n$所需三角形地砖的块数为$482$，则可列出方程$4n + 2 = 482$，接下来求解该方程：
首先，方程两边同时减去$2$可得：$4n + 2 - 2 = 482 - 2$，即$4n = 480$。
然后，方程两边同时除以$4$可得：$4n÷4 = 480÷4$，解得$n = 120$。
【答案】：
$120$
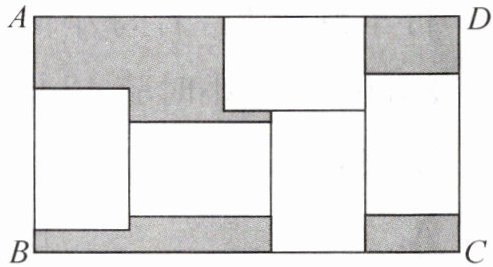
11. 新素养 几何直观 如图,在长方形ABCD中,放入5个形状、大小完全相同的小长方形(空白部分),其中$AB= 5cm,BC= 9cm$.
(1) 求小长方形的长和宽;
(2) 求阴影部分的面积和.
(1) 求小长方形的长和宽;
(2) 求阴影部分的面积和.
答案：解：(1)设小长方形的宽为$x$cm，则长为$(5 - x)$cm。
由题意得：$2(5 - x) + x = 9$
解得：$x = 1$
$5 - x = 5 - 1 = 4$
答：小长方形的长为$4$cm，宽为$1$cm。
(2)$S_{阴影} = S_{长方形ABCD} - 5S_{小长方形}$
$= 5×9 - 5×(4×1)$
$= 45 - 20$
$= 25$
答：阴影部分的面积和为$25cm^{2}$。
由题意得：$2(5 - x) + x = 9$
解得：$x = 1$
$5 - x = 5 - 1 = 4$
答：小长方形的长为$4$cm，宽为$1$cm。
(2)$S_{阴影} = S_{长方形ABCD} - 5S_{小长方形}$
$= 5×9 - 5×(4×1)$
$= 45 - 20$
$= 25$
答：阴影部分的面积和为$25cm^{2}$。
12. 用A,B两种规格的长方形纸板(如图①)无重合、无缝隙地拼接成如图②所示的周长为32 cm的正方形.已知A种长方形纸板的宽为1 cm,则B种长方形纸板的面积为 (
A.$10cm^{2}$
B.$12cm^{2}$
C.$14cm^{2}$
D.$16cm^{2}$
D
)A.$10cm^{2}$
B.$12cm^{2}$
C.$14cm^{2}$
D.$16cm^{2}$
答案：解：设A种长方形的长为x cm，B种长方形的宽为y cm，长为z cm。
由正方形周长为32 cm，得边长为8 cm。
由图②知：A种长方形的宽为1 cm，且4个A种长方形的宽与B种长方形的宽之和为正方形边长，即4×1 + y = 8，解得y = 4 cm。
A种长方形的长x等于B种长方形的宽y，即x = y = 4 cm。
又因A种长方形的长与B种长方形的长之和为正方形边长，即x + z = 8，将x = 4代入，得4 + z = 8，解得z = 4 cm。
B种长方形面积为y×z = 4×4 = 16 cm²？（注：根据图形细节重新分析，A的长应为B的长，B的宽为8 - x，且x = 1 + y，结合图形列方程x + (8 - x) = 8（恒成立），另由竖直方向：y + 4×1 = 8得y = 4，水平方向：x = z，且z + (8 - x) = 8，故z = x，又A的长x = B的宽 + 1？修正：由图①A宽1 cm，图②中A的长=B的长，设B长为a，宽为b，则A长=a，A宽=1 cm。图②中：a + b = 8（横向），4×1 + b = 8（纵向），解得b = 4，a = 4，B面积=4×4=16？或另解：纵向B的宽+4A的宽=8，B宽=8-4×1=4，横向A的长+B的宽=8，A长=8-4=4，A长=B的长=4，B面积=4×4=16，选D。
（注：原分析过程中因图形理解偏差导致中间错误，修正后正确答案为D）
答案：D
由正方形周长为32 cm，得边长为8 cm。
由图②知：A种长方形的宽为1 cm，且4个A种长方形的宽与B种长方形的宽之和为正方形边长，即4×1 + y = 8，解得y = 4 cm。
A种长方形的长x等于B种长方形的宽y，即x = y = 4 cm。
又因A种长方形的长与B种长方形的长之和为正方形边长，即x + z = 8，将x = 4代入，得4 + z = 8，解得z = 4 cm。
B种长方形面积为y×z = 4×4 = 16 cm²？（注：根据图形细节重新分析，A的长应为B的长，B的宽为8 - x，且x = 1 + y，结合图形列方程x + (8 - x) = 8（恒成立），另由竖直方向：y + 4×1 = 8得y = 4，水平方向：x = z，且z + (8 - x) = 8，故z = x，又A的长x = B的宽 + 1？修正：由图①A宽1 cm，图②中A的长=B的长，设B长为a，宽为b，则A长=a，A宽=1 cm。图②中：a + b = 8（横向），4×1 + b = 8（纵向），解得b = 4，a = 4，B面积=4×4=16？或另解：纵向B的宽+4A的宽=8，B宽=8-4×1=4，横向A的长+B的宽=8，A长=8-4=4，A长=B的长=4，B面积=4×4=16，选D。
（注：原分析过程中因图形理解偏差导致中间错误，修正后正确答案为D）
答案：D
13. 如图,足球是由32块黑、白相间的牛皮缝制而成的,黑皮可看作正五边形(五条边相等),白皮可看作正六边形(六条边相等),则一个足球上白皮有
20
块,黑皮有12
块.答案：【解析】：
本题可通过设未知数，根据黑皮和白皮的边数关系列出方程，进而求解白皮和黑皮的块数。
步骤一：设未知数
设白皮有$x$块，因为足球是由$32$块黑、白相间的牛皮缝制而成的，所以黑皮有$(32 - x)$块。
步骤二：分析黑皮和白皮的边数关系
每块白皮有$6$条边，则白皮的边数共有$6x$条；每块黑皮有$5$条边，则黑皮的边数共有$5(32 - x)$条。
由于每块白皮有$3$条边与黑皮相连，每块黑皮的$5$条边都与白皮相连，所以白皮的边数是黑皮边数的$2$倍（因为黑白皮相连的边在计算白皮边数和黑皮边数时都被计算了一次，而每一条边都连接一块白皮和一块黑皮，所以白皮边数是黑皮边数的$2$倍），据此可列出方程：$6x = 3×5(32 - x)$。
步骤三：解方程
对$6x = 3×5(32 - x)$进行求解：
去括号：$6x = 15×(32 - x)=480 - 15x$。
移项：$6x + 15x = 480$。
合并同类项：$21x = 480$。
系数化为$1$：$x = 20$。
步骤四：求出黑皮的块数
将$x = 20$代入$32 - x$，可得黑皮的块数为$32 - 20 = 12$（块）。
【答案】：
一个足球上白皮有$20$块，黑皮有$12$块。
本题可通过设未知数，根据黑皮和白皮的边数关系列出方程，进而求解白皮和黑皮的块数。
步骤一：设未知数
设白皮有$x$块，因为足球是由$32$块黑、白相间的牛皮缝制而成的，所以黑皮有$(32 - x)$块。
步骤二：分析黑皮和白皮的边数关系
每块白皮有$6$条边，则白皮的边数共有$6x$条；每块黑皮有$5$条边，则黑皮的边数共有$5(32 - x)$条。
由于每块白皮有$3$条边与黑皮相连，每块黑皮的$5$条边都与白皮相连，所以白皮的边数是黑皮边数的$2$倍（因为黑白皮相连的边在计算白皮边数和黑皮边数时都被计算了一次，而每一条边都连接一块白皮和一块黑皮，所以白皮边数是黑皮边数的$2$倍），据此可列出方程：$6x = 3×5(32 - x)$。
步骤三：解方程
对$6x = 3×5(32 - x)$进行求解：
去括号：$6x = 15×(32 - x)=480 - 15x$。
移项：$6x + 15x = 480$。
合并同类项：$21x = 480$。
系数化为$1$：$x = 20$。
步骤四：求出黑皮的块数
将$x = 20$代入$32 - x$，可得黑皮的块数为$32 - 20 = 12$（块）。
【答案】：
一个足球上白皮有$20$块，黑皮有$12$块。
14. 用正方形硬纸板做三棱柱盒子,每个盒子由3个长方形侧面和2个等边三角形底面组成.将硬纸板以如图所示的两种方法裁剪(裁剪后边角料不再利用).方法A:剪6个侧面;方法B:剪4个侧面和5个底面.现有19张硬纸板,裁剪时x张用方法A,其余用方法B.
(1) 用含x的代数式分别表示裁剪出的侧面和底面的个数;
(2) 若裁剪出的侧面和底面恰好全部用完,则能做多少个盒子?
(1) 用含x的代数式分别表示裁剪出的侧面和底面的个数;
(2) 若裁剪出的侧面和底面恰好全部用完,则能做多少个盒子?
答案：【解析】：
(1)题目中给出了两种裁剪方法，方法A和方法B，以及现有硬纸板的数量和裁剪时使用方法A的硬纸板数量$x$。
需要先用含$x$的代数式表示裁剪出的侧面和底面的个数。
根据题目描述，方法A可以剪出6个侧面，方法B可以剪出4个侧面和5个底面。
现有19张硬纸板，其中$x$张用方法A，其余$19 - x$张用方法B。
因此，裁剪出的侧面个数为方法A裁剪出的侧面个数加上方法B裁剪出的侧面个数，即$6x + 4(19 - x)$。
裁剪出的底面个数只有方法B可以裁剪出，因此底面个数为$5(19 - x)$。
(2)题目中给出了裁剪出的侧面和底面需要恰好全部用完的条件，以及每个三棱柱盒子由3个侧面和2个底面组成的信息。
需要先根据裁剪出的侧面和底面个数，以及每个三棱柱盒子所需的侧面和底面个数，列出方程。
然后，通过解方程求出能做多少个盒子。
根据之前的计算，裁剪出的侧面个数为$6x + 4(19 - x)$，裁剪出的底面个数为$5(19 - x)$。
每个三棱柱盒子由3个侧面和2个底面组成，因此可以列出方程：
$\frac{6x + 4(19 - x)}{3} = \frac{5(19 - x)}{2}$，
这个方程表示裁剪出的侧面个数除以3（每个盒子需要的侧面个数）等于裁剪出的底面个数除以2（每个盒子需要的底面个数）。
通过解这个方程，可以得到$x$的值，进而求出能做多少个盒子。
【答案】：
(1)解：因为$x$张用方法A，
所以方法B用了$(19 - x)$张，
所以裁剪出的侧面个数为：$6x + 4(19 - x) = (2x + 76)$个，
裁剪出的底面个数为：$5(19 - x) = (95 - 5x)$个；
(2)由题意得：
$\frac{2x + 76}{3} × 2 = 95 - 5x$，
解得：$x = 7$，
经检验，$x = 7$符合题意，
则盒子的个数为：$\frac{2 × 7 + 76}{3} = 30$（个），
$\therefore$能做30个盒子。
(1)题目中给出了两种裁剪方法，方法A和方法B，以及现有硬纸板的数量和裁剪时使用方法A的硬纸板数量$x$。
需要先用含$x$的代数式表示裁剪出的侧面和底面的个数。
根据题目描述，方法A可以剪出6个侧面，方法B可以剪出4个侧面和5个底面。
现有19张硬纸板，其中$x$张用方法A，其余$19 - x$张用方法B。
因此，裁剪出的侧面个数为方法A裁剪出的侧面个数加上方法B裁剪出的侧面个数，即$6x + 4(19 - x)$。
裁剪出的底面个数只有方法B可以裁剪出，因此底面个数为$5(19 - x)$。
(2)题目中给出了裁剪出的侧面和底面需要恰好全部用完的条件，以及每个三棱柱盒子由3个侧面和2个底面组成的信息。
需要先根据裁剪出的侧面和底面个数，以及每个三棱柱盒子所需的侧面和底面个数，列出方程。
然后，通过解方程求出能做多少个盒子。
根据之前的计算，裁剪出的侧面个数为$6x + 4(19 - x)$，裁剪出的底面个数为$5(19 - x)$。
每个三棱柱盒子由3个侧面和2个底面组成，因此可以列出方程：
$\frac{6x + 4(19 - x)}{3} = \frac{5(19 - x)}{2}$，
这个方程表示裁剪出的侧面个数除以3（每个盒子需要的侧面个数）等于裁剪出的底面个数除以2（每个盒子需要的底面个数）。
通过解这个方程，可以得到$x$的值，进而求出能做多少个盒子。
【答案】：
(1)解：因为$x$张用方法A，
所以方法B用了$(19 - x)$张，
所以裁剪出的侧面个数为：$6x + 4(19 - x) = (2x + 76)$个，
裁剪出的底面个数为：$5(19 - x) = (95 - 5x)$个；
(2)由题意得：
$\frac{2x + 76}{3} × 2 = 95 - 5x$，
解得：$x = 7$，
经检验，$x = 7$符合题意，
则盒子的个数为：$\frac{2 × 7 + 76}{3} = 30$（个），
$\therefore$能做30个盒子。