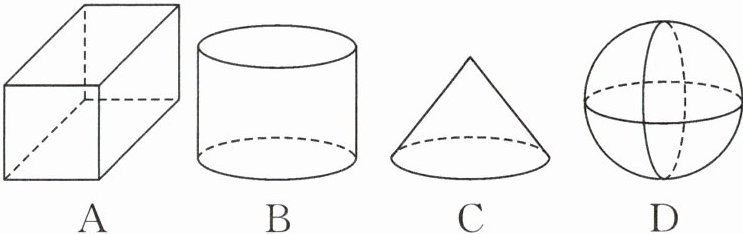
1. (2023·四川乐山)下面的几何体中,是圆柱的为 (
B
)
答案:解:圆柱是由两个大小相等、相互平行的圆形(底面)以及连接两个底面的一个曲面(侧面)围成的几何体。观察各选项:
选项A为长方体,不符合圆柱特征;
选项B符合圆柱的定义,是圆柱;
选项C为圆锥,不符合圆柱特征;
选项D为球体,不符合圆柱特征。
答案:B
选项A为长方体,不符合圆柱特征;
选项B符合圆柱的定义,是圆柱;
选项C为圆锥,不符合圆柱特征;
选项D为球体,不符合圆柱特征。
答案:B
2. 新素养 几何直观 下列立体图形中,每个面都是平面的为 (
A
)答案:【解析】:本题考查对立体图形的认识,我们需要根据图形的特点,判断每个选项中的立体图形是否每个面都是平面的。
A选项长方体有六个面,每个面都是平面,符合题意;
B选项圆柱有两个平面(上下底面)和一个曲面(侧面),不符合题意;
C选项球体没有平面,整个球体是一个曲面,不符合题意;
D选项圆锥有一个平面(底面)和一个曲面(侧面),不符合题意。
【答案】:A
A选项长方体有六个面,每个面都是平面,符合题意;
B选项圆柱有两个平面(上下底面)和一个曲面(侧面),不符合题意;
C选项球体没有平面,整个球体是一个曲面,不符合题意;
D选项圆锥有一个平面(底面)和一个曲面(侧面),不符合题意。
【答案】:A
3. (2025·江苏徐州期末)如果一个棱柱有10个面,那么它的棱数是 (
A.16
B.20
C.22
D.24
D
)A.16
B.20
C.22
D.24
答案:解:因为棱柱有10个面,其中上下2个底面,所以侧面有10 - 2 = 8个。
则该棱柱为八棱柱。
八棱柱有8条侧棱,上下底面各有8条棱,所以总棱数为8×3 = 24。
答案:D
则该棱柱为八棱柱。
八棱柱有8条侧棱,上下底面各有8条棱,所以总棱数为8×3 = 24。
答案:D
4. 某个直棱柱所有侧棱的长度之和为60cm,小明量得其中一条侧棱的长为10cm,则这个直棱柱有
6
条侧棱,其底面的形状是六边形
。答案:【解析】:
题目考查直棱柱的性质,特别是侧棱的性质以及底面形状与侧棱数量的关系。
直棱柱的所有侧棱长度相等,由此可以计算出侧棱的数量。
再根据侧棱数量与底面形状的关系,确定底面的形状。
所有侧棱长度之和为60cm,其中一条侧棱的长为10cm,
所以侧棱的数量为:$60 ÷ 10 = 6$(条)。
由于直棱柱的底面形状与侧棱数量有直接关系,
六条侧棱意味着底面是一个六边形。
【答案】:
6;六边形。
题目考查直棱柱的性质,特别是侧棱的性质以及底面形状与侧棱数量的关系。
直棱柱的所有侧棱长度相等,由此可以计算出侧棱的数量。
再根据侧棱数量与底面形状的关系,确定底面的形状。
所有侧棱长度之和为60cm,其中一条侧棱的长为10cm,
所以侧棱的数量为:$60 ÷ 10 = 6$(条)。
由于直棱柱的底面形状与侧棱数量有直接关系,
六条侧棱意味着底面是一个六边形。
【答案】:
6;六边形。
5. 给出下列说法:
① 柱体的两个底面一样大;
② 圆柱、圆锥的底面都是圆;
③ 棱柱的底面是四边形;
④ 棱柱的侧面一定是长方形;
⑤ 长方体一定是柱体;
⑥ 长方体的所有面都不可能是正方形。
其中正确的有
① 柱体的两个底面一样大;
② 圆柱、圆锥的底面都是圆;
③ 棱柱的底面是四边形;
④ 棱柱的侧面一定是长方形;
⑤ 长方体一定是柱体;
⑥ 长方体的所有面都不可能是正方形。
其中正确的有
3
个。答案:解:①柱体的两个底面一样大,正确;
②圆柱、圆锥的底面都是圆,正确;
③棱柱的底面可以是三角形、四边形等多边形,故错误;
④棱柱的侧面一定是平行四边形,不一定是长方形,故错误;
⑤长方体一定是柱体,正确;
⑥长方体的面可能有正方形,故错误。
正确的有①②⑤,共3个。
答案:3
②圆柱、圆锥的底面都是圆,正确;
③棱柱的底面可以是三角形、四边形等多边形,故错误;
④棱柱的侧面一定是平行四边形,不一定是长方形,故错误;
⑤长方体一定是柱体,正确;
⑥长方体的面可能有正方形,故错误。
正确的有①②⑤,共3个。
答案:3
6. (1) 正方体有
(2) 圆柱有
(3) 若一个直棱柱的底面是七边形,则它的侧面共有
6
个面,8
个顶点,12
条棱,这些棱的长度相等
(填“相等”或“不相等”);(2) 圆柱有
3
个面,其中有2
个平面,还有1个面是曲
面;(3) 若一个直棱柱的底面是七边形,则它的侧面共有
7
个长方形,它一共有9
个面。答案:【解析】:
本题主要考察了对几何图形基本性质的理解,包括正方体、圆柱和直棱柱的面、顶点和棱的数量及特性。
(1) 正方体是一个有6个面、12个顶点和12条棱的几何体,且所有棱的长度都相等。
(2) 圆柱由两个平面和一个曲面组成,其中两个平面是圆柱的上下底面,曲面是圆柱的侧面。
(3) 对于直棱柱,其侧面数量与底面的边数相同,因此底面是七边形的直棱柱有7个侧面,再加上上下两个底面,总共9个面。
【答案】:
(1) 6;8;12;相等
(2) 3;2;曲
(3) 7;9
本题主要考察了对几何图形基本性质的理解,包括正方体、圆柱和直棱柱的面、顶点和棱的数量及特性。
(1) 正方体是一个有6个面、12个顶点和12条棱的几何体,且所有棱的长度都相等。
(2) 圆柱由两个平面和一个曲面组成,其中两个平面是圆柱的上下底面,曲面是圆柱的侧面。
(3) 对于直棱柱,其侧面数量与底面的边数相同,因此底面是七边形的直棱柱有7个侧面,再加上上下两个底面,总共9个面。
【答案】:
(1) 6;8;12;相等
(2) 3;2;曲
(3) 7;9
7. 新趋势 开放探究 请将下列几何体进行分类,并说出分类的依据。


答案:解:分类一:按是否有曲面分
有曲面:①②⑦
无曲面:③④⑤⑥⑧
依据:几何体表面是否包含曲面
分类二:按柱体、锥体、球体分
柱体:①③④⑤⑥⑧
锥体:②
球体:⑦
依据:几何体的基本类型特征
分类三:按是否由平面围成分
由平面围成:③④⑤⑥⑧
不由平面围成(含曲面):①②⑦
依据:几何体表面是否全部为平面
有曲面:①②⑦
无曲面:③④⑤⑥⑧
依据:几何体表面是否包含曲面
分类二:按柱体、锥体、球体分
柱体:①③④⑤⑥⑧
锥体:②
球体:⑦
依据:几何体的基本类型特征
分类三:按是否由平面围成分
由平面围成:③④⑤⑥⑧
不由平面围成(含曲面):①②⑦
依据:几何体表面是否全部为平面
8. 下列棱柱中,和九棱锥的棱数相等的是 (
A.五棱柱
B.六棱柱
C.七棱柱
D.八棱柱
B
)A.五棱柱
B.六棱柱
C.七棱柱
D.八棱柱
答案:解:九棱锥有9条侧棱,底面为九边形有9条棱,总棱数为9+9=18条。
五棱柱有5×3=15条棱;六棱柱有6×3=18条棱;七棱柱有7×3=21条棱;八棱柱有8×3=24条棱。
所以和九棱锥棱数相等的是六棱柱。
答案:B
五棱柱有5×3=15条棱;六棱柱有6×3=18条棱;七棱柱有7×3=21条棱;八棱柱有8×3=24条棱。
所以和九棱锥棱数相等的是六棱柱。
答案:B
9. 下面的立体图形中,有五个面的是 (
A.四棱锥
B.五棱锥
C.四棱柱
D.五棱柱
A
)A.四棱锥
B.五棱锥
C.四棱柱
D.五棱柱
答案:【解析】:
本题考查对立体图形的认识,需要知道四棱锥、五棱锥、四棱柱和五棱柱的基本结构特征。
四棱锥由一个四边形底面和四个三角形侧面组成,共五个面。
五棱锥由一个五边形底面和五个三角形侧面组成,共六个面。
四棱柱由两个四边形底面和四个矩形侧面组成,共六个面。
五棱柱由两个五边形底面和五个矩形侧面组成,共七个面。
根据这些信息,可以判断出有五个面的立体图形是四棱锥。
【答案】:
A
本题考查对立体图形的认识,需要知道四棱锥、五棱锥、四棱柱和五棱柱的基本结构特征。
四棱锥由一个四边形底面和四个三角形侧面组成,共五个面。
五棱锥由一个五边形底面和五个三角形侧面组成,共六个面。
四棱柱由两个四边形底面和四个矩形侧面组成,共六个面。
五棱柱由两个五边形底面和五个矩形侧面组成,共七个面。
根据这些信息,可以判断出有五个面的立体图形是四棱锥。
【答案】:
A
10. 一个正方体锯掉一个角后,剩下几何体的顶点个数是 (
A.7
B.8
C.9
D.7或8或9或10
D
)A.7
B.8
C.9
D.7或8或9或10
答案:解:正方体原有8个顶点。锯掉一个角时:
情况1:截面不过原顶点,增加3个顶点,此时顶点数为8 - 1 + 3 = 10;
情况2:截面过1个原顶点,增加2个顶点,此时顶点数为8 - 1 + 2 = 9;
情况3:截面过2个原顶点,增加1个顶点,此时顶点数为8 - 1 + 1 = 8;
情况4:截面过3个原顶点,不增加顶点,此时顶点数为8 - 1 + 0 = 7。
综上,剩下几何体的顶点个数是7或8或9或10。
D
情况1:截面不过原顶点,增加3个顶点,此时顶点数为8 - 1 + 3 = 10;
情况2:截面过1个原顶点,增加2个顶点,此时顶点数为8 - 1 + 2 = 9;
情况3:截面过2个原顶点,增加1个顶点,此时顶点数为8 - 1 + 1 = 8;
情况4:截面过3个原顶点,不增加顶点,此时顶点数为8 - 1 + 0 = 7。
综上,剩下几何体的顶点个数是7或8或9或10。
D