11. 如图,小明在一个有盖可密封的透明正方体玻璃盒子里装了一定量的水,他不断改变正方体盒子的放置方式(假设盒子可以采用任何方式放置),盒子里的水便形成不同的几何体。给出下列选项:① 长方体;② 正方体;③ 圆柱;④ 三棱锥;⑤ 三棱柱。其中可能是盒子里的水形成的几何体的为______。(填序号)
①⑤
答案:解:①⑤
12. 用三根铁丝把一个长6dm、宽4dm、高2dm的木箱捆起来(如图所示),打结处各用1dm铁丝,则这三根铁丝的总长至少为
51
dm。答案:【解析】:
本题主要考查了空间几何图形的认识以及周长的计算,需要计算出围绕木箱不同方向的三根铁丝的长度,再求和,最后加上打结处的长度,
从图中可以看出,三根铁丝分别沿着木箱的三个不同方向捆绑,
第一根铁丝沿着长和宽的方向,其长度为木箱两个长和两个宽的和,即$2×(6+4)=20$(dm),
第二根铁丝沿着长和高的方向,其长度为木箱两个长和两个高的和,即$2×(6+2)=16$(dm),
第三根铁丝沿着宽和高的方向,其长度为木箱两个宽和两个高的和,即$2×(4+2)=12$(dm),
由于打结处各用1dm铁丝,且有三处打结,所以打结处总共用去的铁丝长度为$3×1=3$(dm),
因此,三根铁丝的总长至少为:$20+16+12+3=51$(dm)。
【答案】:51。
本题主要考查了空间几何图形的认识以及周长的计算,需要计算出围绕木箱不同方向的三根铁丝的长度,再求和,最后加上打结处的长度,
从图中可以看出,三根铁丝分别沿着木箱的三个不同方向捆绑,
第一根铁丝沿着长和宽的方向,其长度为木箱两个长和两个宽的和,即$2×(6+4)=20$(dm),
第二根铁丝沿着长和高的方向,其长度为木箱两个长和两个高的和,即$2×(6+2)=16$(dm),
第三根铁丝沿着宽和高的方向,其长度为木箱两个宽和两个高的和,即$2×(4+2)=12$(dm),
由于打结处各用1dm铁丝,且有三处打结,所以打结处总共用去的铁丝长度为$3×1=3$(dm),
因此,三根铁丝的总长至少为:$20+16+12+3=51$(dm)。
【答案】:51。
13. 若将棱长为n(n>1,n为整数)的正方体切成$n^3$个棱长为1的小正方体,则所有小正方体表面积的和是原正方体表面积的
n
倍。答案:解:原正方体表面积为$6n^2$。
每个小正方体表面积为$6×1^2 = 6$,小正方体总个数为$n^3$,所有小正方体表面积的和为$6n^3$。
倍数为$\frac{6n^3}{6n^2}=n$。
答案:$n$
每个小正方体表面积为$6×1^2 = 6$,小正方体总个数为$n^3$,所有小正方体表面积的和为$6n^3$。
倍数为$\frac{6n^3}{6n^2}=n$。
答案:$n$
14. 如图是由两个相同的小正方体拼成的一个长方体。若该长方体的体积为$1024cm^3,$求该长方体的表面积。
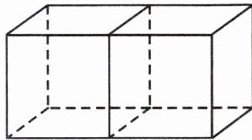

答案:【解析】:本题主要考查了正方体和长方体的体积和表面积的计算。
先设小正方体的边长为 a cm。
根据题意,两个正方体拼成的长方体的体积是两个正方体体积之和,即:
$2a^3=1024$($cm^3$),
解这个方程求出 a 的值,
$a^3=512$,
$a=\sqrt[3]{512}=8$(cm),
长方体的长、宽、高分别为 a,a,2a。
长方体的表面积公式为$2(长×宽+长×高+宽×高)$,
代入 a 的值得长方体的表面积为:
$2(a× a+a× 2a+a× 2a)=2(a^2+2a^2+2a^2)=2× 5a^2=10a^2=10× 8^2=640$($cm^2$),
【答案】:$\begin{aligned}\therefore该长方体的表面积为640cm^2。\end{aligned}$
先设小正方体的边长为 a cm。
根据题意,两个正方体拼成的长方体的体积是两个正方体体积之和,即:
$2a^3=1024$($cm^3$),
解这个方程求出 a 的值,
$a^3=512$,
$a=\sqrt[3]{512}=8$(cm),
长方体的长、宽、高分别为 a,a,2a。
长方体的表面积公式为$2(长×宽+长×高+宽×高)$,
代入 a 的值得长方体的表面积为:
$2(a× a+a× 2a+a× 2a)=2(a^2+2a^2+2a^2)=2× 5a^2=10a^2=10× 8^2=640$($cm^2$),
【答案】:$\begin{aligned}\therefore该长方体的表面积为640cm^2。\end{aligned}$
15. 底面积相等的圆柱和圆锥,它们的体积比是1:2。若圆锥的高是9cm,则圆柱的高是 (
A.3cm
B.1.5cm
C.18cm
D.24cm
B
)A.3cm
B.1.5cm
C.18cm
D.24cm
答案:【解析】:
此题主要考查了圆柱和圆锥的体积公式。
首先,我们需要知道圆柱和圆锥的体积公式:
圆柱的体积 $V_{cylinder} = \pi r^{2} h_{cylinder}$,
圆锥的体积 $V_{cone} = \frac{1}{3} \pi r^{2} h_{cone}$,
题目告诉我们圆柱和圆锥的底面积相等,即它们的半径 $r$ 是相等的。
同时,题目还给出了它们的体积比为 1:2,以及圆锥的高 $h_{cone}$ 是 9cm。
设圆柱的高为 $h_{cylinder}$,根据题目给出的体积比,我们可以列出以下比例:
$\frac{V_{cylinder}}{V_{cone}} = \frac{1}{2}$,
代入体积公式,我们得到:
$\frac{\pi r^{2} h_{cylinder}}{\frac{1}{3} \pi r^{2} × 9} = \frac{1}{2}$,
由于 $\pi r^{2}$ 在分子和分母中都有,可以相互抵消,化简后得到:
$\frac{h_{cylinder}}{3} = \frac{1}{2} × \frac{1}{3} × 9$,
进一步计算,得到 $h_{cylinder} = 1.5$cm。
【答案】:
B.1.5cm。
此题主要考查了圆柱和圆锥的体积公式。
首先,我们需要知道圆柱和圆锥的体积公式:
圆柱的体积 $V_{cylinder} = \pi r^{2} h_{cylinder}$,
圆锥的体积 $V_{cone} = \frac{1}{3} \pi r^{2} h_{cone}$,
题目告诉我们圆柱和圆锥的底面积相等,即它们的半径 $r$ 是相等的。
同时,题目还给出了它们的体积比为 1:2,以及圆锥的高 $h_{cone}$ 是 9cm。
设圆柱的高为 $h_{cylinder}$,根据题目给出的体积比,我们可以列出以下比例:
$\frac{V_{cylinder}}{V_{cone}} = \frac{1}{2}$,
代入体积公式,我们得到:
$\frac{\pi r^{2} h_{cylinder}}{\frac{1}{3} \pi r^{2} × 9} = \frac{1}{2}$,
由于 $\pi r^{2}$ 在分子和分母中都有,可以相互抵消,化简后得到:
$\frac{h_{cylinder}}{3} = \frac{1}{2} × \frac{1}{3} × 9$,
进一步计算,得到 $h_{cylinder} = 1.5$cm。
【答案】:
B.1.5cm。
16. 一个六棱柱共有
18
条棱。如果它的底面边长都是2cm,侧棱长都是4cm,那么它所有棱长的和是48
cm。答案:【解析】:
题目考查了七年级数学中关于几何体棱数的计算以及棱长之和的计算。
首先,需要知道一个六棱柱的基本结构,它有两个六边形的底面,每个六边形有6条边,再加上6条连接这两个底面的侧棱。
所以,六棱柱的棱数可以通过计算得出:底面的边数$×$ 2(两个底面)$+$侧棱数。
接着,根据题目给出的底面边长和侧棱长,可以计算出所有棱长的和。
【答案】:
一个六棱柱共有$18$条棱($6$条底边$× 2+6$条侧棱$=18$条棱)。
所有棱长的和为:$6 × 2 × 2+ 4 × 6 = 48(cm)$。(其中底面边长棱长和为$6 × 2 × 2$,侧棱长和为$4 × 6$)
故答案为:$18$;$48$。
题目考查了七年级数学中关于几何体棱数的计算以及棱长之和的计算。
首先,需要知道一个六棱柱的基本结构,它有两个六边形的底面,每个六边形有6条边,再加上6条连接这两个底面的侧棱。
所以,六棱柱的棱数可以通过计算得出:底面的边数$×$ 2(两个底面)$+$侧棱数。
接着,根据题目给出的底面边长和侧棱长,可以计算出所有棱长的和。
【答案】:
一个六棱柱共有$18$条棱($6$条底边$× 2+6$条侧棱$=18$条棱)。
所有棱长的和为:$6 × 2 × 2+ 4 × 6 = 48(cm)$。(其中底面边长棱长和为$6 × 2 × 2$,侧棱长和为$4 × 6$)
故答案为:$18$;$48$。
17. 新趋势 推导探究 (2025·江苏淮安期末)由若干个平面围成的几何体叫作多面体,有几个面,就叫作几面体。面与面的交线叫作棱,棱与棱的交点叫作顶点。三棱锥有四个面,所以三棱锥又叫作四面体。正方体又叫作
(1) 探究:如果把一个多面体的顶点数记为V,面数记为F,棱数记为E,请完成下表:
| | V | F | E | V+F-E |
| 四面体 |
| 长方体 |
| 五棱柱 |
(2) 猜想:通过以上探究,你能得到一个什么结论?
(3) 验证:在课本的插图中再找出一个多面体,数一数它分别有几个顶点、几个面和几条棱,看一看顶点数、面数和棱数是否仍满足上述关系;
(4) 应用:(2)中的结论对所有的多面体都成立,数学家欧拉证明了这个关系式,所以上述关系式叫作欧拉公式。想一想,是否存在一个多面体,它有10个面、30条棱和20个顶点?
六
面体,有五条侧棱的棱柱又叫作七
面体。(1) 探究:如果把一个多面体的顶点数记为V,面数记为F,棱数记为E,请完成下表:
| | V | F | E | V+F-E |
| 四面体 |
4
| 4
| 6
| 2
|| 长方体 |
8
| 6
| 12
| 2
|| 五棱柱 |
10
| 7
| 15
| 2
|(2) 猜想:通过以上探究,你能得到一个什么结论?
能得到的结论是:对于任意多面体,其顶点数V、面数F和棱数E之间都满足关系V+F-E=2。
(3) 验证:在课本的插图中再找出一个多面体,数一数它分别有几个顶点、几个面和几条棱,看一看顶点数、面数和棱数是否仍满足上述关系;
验证过程略(选择其他多面体进行验证,结果满足上述关系)。
(4) 应用:(2)中的结论对所有的多面体都成立,数学家欧拉证明了这个关系式,所以上述关系式叫作欧拉公式。想一想,是否存在一个多面体,它有10个面、30条棱和20个顶点?
不存在一个多面体,它有10个面、30条棱和20个顶点。
答案:【解析】:
本题主要考查多面体的基本概念以及欧拉公式的应用。
首先,需要理解多面体的面、棱、顶点的定义,并知道正方体和五棱柱分别有多少面。
接着,通过填写表格来探究多面体的顶点数V、面数F、棱数E之间的关系。
然后,根据探究结果猜想一个结论,并通过验证其他多面体来确认这个结论。
最后,应用这个结论来判断是否存在一个具有特定面数、棱数和顶点数的多面体。
(1)对于正方体,它有6个面,所以又叫作六面体。
对于有五条侧棱的棱柱,它总共有7个面(2个底面和5个侧面),所以又叫作七面体。
接下来,填写表格:
四面体:V=4(因为有4个顶点),F=4(因为有4个面),E=6(因为有6条棱,每条棱由两个顶点确定,但每条棱被两个面共享,所以总棱数为$\frac{4 × 3}{2} = 6$),$V+F-E=4+4-6=2$。
长方体:V=8(因为有8个顶点),F=6(因为有6个面),E=12(因为有12条棱,每个顶点连接3条棱,但每条棱被两个顶点共享,所以总棱数为$\frac{8 × 3}{2} = 12$),$V+F-E=8+6-12=2$。
五棱柱:V=10(底面5个顶点,顶面5个顶点),F=7(2个底面和5个侧面),$E=15$(底面5条棱,顶面5条棱,连接底面和顶面的5条棱,但每条棱被两个面共享,底面与顶面的棱不共享,所以总棱数为$5+5+5=15$),$V+F-E=10+7-15=2$。
(2)通过观察表格,可以发现对于四面体、长方体和五棱柱,都有$V+F-E=2$,可以猜想:对于任意多面体,其顶点数V、面数F和棱数E之间都满足关系$V+F-E=2$。
(3)为了验证这个猜想,可以选择一个多面体,如三棱柱,来数一数它的顶点数、面数和棱数。
三棱柱有6个顶点,5个面(2个底面和3个侧面),9条棱(底面3条,顶面3条,连接底面和顶面的3条)。
验证得:$V+F-E=6+5-9=2$,满足上述关系。
(4)根据欧拉公式$V+F-E=2$,可以判断是否存在一个多面体,它有10个面、30条棱和20个顶点。
将给定的值代入公式:$20+10-30=0 \neq 2$。
因此,不存在这样一个多面体。
【答案】:
(1)六;七;填表如下:
| | V | F | E | V+F-E |
| --- | --- | --- | --- | --- |
| 四面体 | 4 | 4 | 6 | 2 |
| 长方体 | 8 | 6 | 12 | 2 |
| 五棱柱 | 10 | 7 | 15 | 2 |
(2)能得到的结论是:对于任意多面体,其顶点数V、面数F和棱数E之间都满足关系$V+F-E=2$。
(3)验证过程略(选择其他多面体进行验证,结果满足上述关系)。
(4)不存在一个多面体,它有10个面、30条棱和20个顶点。
本题主要考查多面体的基本概念以及欧拉公式的应用。
首先,需要理解多面体的面、棱、顶点的定义,并知道正方体和五棱柱分别有多少面。
接着,通过填写表格来探究多面体的顶点数V、面数F、棱数E之间的关系。
然后,根据探究结果猜想一个结论,并通过验证其他多面体来确认这个结论。
最后,应用这个结论来判断是否存在一个具有特定面数、棱数和顶点数的多面体。
(1)对于正方体,它有6个面,所以又叫作六面体。
对于有五条侧棱的棱柱,它总共有7个面(2个底面和5个侧面),所以又叫作七面体。
接下来,填写表格:
四面体:V=4(因为有4个顶点),F=4(因为有4个面),E=6(因为有6条棱,每条棱由两个顶点确定,但每条棱被两个面共享,所以总棱数为$\frac{4 × 3}{2} = 6$),$V+F-E=4+4-6=2$。
长方体:V=8(因为有8个顶点),F=6(因为有6个面),E=12(因为有12条棱,每个顶点连接3条棱,但每条棱被两个顶点共享,所以总棱数为$\frac{8 × 3}{2} = 12$),$V+F-E=8+6-12=2$。
五棱柱:V=10(底面5个顶点,顶面5个顶点),F=7(2个底面和5个侧面),$E=15$(底面5条棱,顶面5条棱,连接底面和顶面的5条棱,但每条棱被两个面共享,底面与顶面的棱不共享,所以总棱数为$5+5+5=15$),$V+F-E=10+7-15=2$。
(2)通过观察表格,可以发现对于四面体、长方体和五棱柱,都有$V+F-E=2$,可以猜想:对于任意多面体,其顶点数V、面数F和棱数E之间都满足关系$V+F-E=2$。
(3)为了验证这个猜想,可以选择一个多面体,如三棱柱,来数一数它的顶点数、面数和棱数。
三棱柱有6个顶点,5个面(2个底面和3个侧面),9条棱(底面3条,顶面3条,连接底面和顶面的3条)。
验证得:$V+F-E=6+5-9=2$,满足上述关系。
(4)根据欧拉公式$V+F-E=2$,可以判断是否存在一个多面体,它有10个面、30条棱和20个顶点。
将给定的值代入公式:$20+10-30=0 \neq 2$。
因此,不存在这样一个多面体。
【答案】:
(1)六;七;填表如下:
| | V | F | E | V+F-E |
| --- | --- | --- | --- | --- |
| 四面体 | 4 | 4 | 6 | 2 |
| 长方体 | 8 | 6 | 12 | 2 |
| 五棱柱 | 10 | 7 | 15 | 2 |
(2)能得到的结论是:对于任意多面体,其顶点数V、面数F和棱数E之间都满足关系$V+F-E=2$。
(3)验证过程略(选择其他多面体进行验证,结果满足上述关系)。
(4)不存在一个多面体,它有10个面、30条棱和20个顶点。