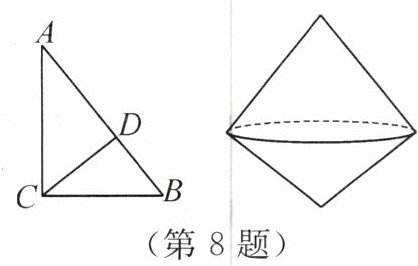
8. 如图, $CD$ 是直角三角形 $ABC$ 的高, 将该三角形按以下方式旋转一周可以得到右侧几何体的是 (
A.绕着边 $AC$ 所在直线旋转
B.绕着边 $AB$ 所在直线旋转
C.绕着高 $CD$ 所在直线旋转
D.绕着边 $BC$ 所在直线旋转
B
) 
A.绕着边 $AC$ 所在直线旋转
B.绕着边 $AB$ 所在直线旋转
C.绕着高 $CD$ 所在直线旋转
D.绕着边 $BC$ 所在直线旋转
答案:【解析】:
本题主要考查空间想象能力以及对旋转体形成原理的理解,需要判断直角三角形$ABC$绕不同边旋转一周后所形成的几何体是否与右侧给出的几何体相符,右侧几何体是由两个共底的圆锥组合而成,所以要分析直角三角形绕各边旋转时,各部分旋转后形成的曲面所构成的几何体形状。
选项A:绕着边$AC$所在直线旋转,直角边$BC$旋转一周形成一个圆锥,而另一条直角边$AB$旋转一周形成的不是圆锥的侧面,所以得到的不是两个共底的圆锥组合体,A选项错误。
选项B:绕着边$AB$所在直线旋转,直角边$AC$和$BC$旋转一周分别形成两个圆锥,这两个圆锥以$CD$为底面半径,以$AD$和$BD$为高,共底,符合右侧几何体的特征,B选项正确。
选项C:绕着高$CD$所在直线旋转,得到的几何体是两个共底的圆锥,但底面半径是$AD$和$BD$,整体形状与右侧几何体不同,C选项错误。
选项D:绕着边$BC$所在直线旋转,直角边$AC$旋转一周形成一个圆锥,另一条直角边$AB$旋转一周形成的不是圆锥的侧面,得到的不是两个共底的圆锥组合体,D选项错误。
【答案】:B
本题主要考查空间想象能力以及对旋转体形成原理的理解,需要判断直角三角形$ABC$绕不同边旋转一周后所形成的几何体是否与右侧给出的几何体相符,右侧几何体是由两个共底的圆锥组合而成,所以要分析直角三角形绕各边旋转时,各部分旋转后形成的曲面所构成的几何体形状。
选项A:绕着边$AC$所在直线旋转,直角边$BC$旋转一周形成一个圆锥,而另一条直角边$AB$旋转一周形成的不是圆锥的侧面,所以得到的不是两个共底的圆锥组合体,A选项错误。
选项B:绕着边$AB$所在直线旋转,直角边$AC$和$BC$旋转一周分别形成两个圆锥,这两个圆锥以$CD$为底面半径,以$AD$和$BD$为高,共底,符合右侧几何体的特征,B选项正确。
选项C:绕着高$CD$所在直线旋转,得到的几何体是两个共底的圆锥,但底面半径是$AD$和$BD$,整体形状与右侧几何体不同,C选项错误。
选项D:绕着边$BC$所在直线旋转,直角边$AC$旋转一周形成一个圆锥,另一条直角边$AB$旋转一周形成的不是圆锥的侧面,得到的不是两个共底的圆锥组合体,D选项错误。
【答案】:B
9. (2025·江苏连云港期末) 如图, 长方形 $ABCD$ 的长为 4, 宽为 3, 则四个小长方形 (阴影部分) 的周长之和为 (
A.7
B.12
C.14
D.16
C
)A.7
B.12
C.14
D.16
答案:【解析】:
此题考查平移性质和长方形周长计算,从图中可以看出阴影部分的四周的线段分别可以平移拼凑,正好是长方形的周长,已知长为$4$,宽为$3$,长方形的周长公式为$C=(a+b)× 2$,其中$a$为长,$b$为宽,所以可以列出$(4+3)× 2=14$,因此四个小长方形的周长之和就等于大长方形的周长。
【答案】:
C
此题考查平移性质和长方形周长计算,从图中可以看出阴影部分的四周的线段分别可以平移拼凑,正好是长方形的周长,已知长为$4$,宽为$3$,长方形的周长公式为$C=(a+b)× 2$,其中$a$为长,$b$为宽,所以可以列出$(4+3)× 2=14$,因此四个小长方形的周长之和就等于大长方形的周长。
【答案】:
C
10. 新趋势 学科融合 如图, 有一个英语单词, 四个字母都关于直线 $l$ 对称, 请你写出这个单词:

BOOK
.
答案:BOOK
11. 小王同学用边长为 $10 \mathrm{~cm}$ 的正方形纸板做了一副七巧板, 拼成如图所示的一座桥, 则桥中阴影部分的面积为 ______ $\mathrm{cm}^2$.


50
答案:【解析】:本题主要考查七巧板以及阴影部分面积的计算。
由图可知,阴影部分为原正方形面积的一半。
原正方形的边长为$10cm$,
根据正方形的面积公式,可得原正方形的面积为:
$S=a^2=10^2=100(cm^2)$,
所以,阴影部分的面积为:
$100{÷} 2=50(cm^2)$。
【答案】:$50$。
由图可知,阴影部分为原正方形面积的一半。
原正方形的边长为$10cm$,
根据正方形的面积公式,可得原正方形的面积为:
$S=a^2=10^2=100(cm^2)$,
所以,阴影部分的面积为:
$100{÷} 2=50(cm^2)$。
【答案】:$50$。
12. 按要求画图: (用阴影表示)
(1) 将图形 $A$ 平移得到图形 $B$;
(2) 将图形 $B$ 沿图中虚线翻折得到图形 $C$;
(3) 将图形 $C$ 绕其右下方的顶点旋转 $180^\circ$ 得到图形 $D$.

(1) 将图形 $A$ 平移得到图形 $B$;
(2) 将图形 $B$ 沿图中虚线翻折得到图形 $C$;
(3) 将图形 $C$ 绕其右下方的顶点旋转 $180^\circ$ 得到图形 $D$.

答案:答案略
解析:
(图形绘制如下,阴影部分表示各变换后的图形)
(1)图形B为图形A平移后的位置,阴影与图形A阴影位置相同。
(2)图形C为图形B沿虚线翻折后的位置,阴影与图形B阴影关于虚线对称。
(3)图形D为图形C绕其右下方顶点旋转$180^\circ$后的位置,阴影与图形C阴影关于旋转中心中心对称。
(注:此处需根据实际图形A的阴影位置及变换要求在答题卡对应位置画出阴影,上述文字描述仅为辅助说明,实际作答以图形阴影为准。)
(1)图形B为图形A平移后的位置,阴影与图形A阴影位置相同。
(2)图形C为图形B沿虚线翻折后的位置,阴影与图形B阴影关于虚线对称。
(3)图形D为图形C绕其右下方顶点旋转$180^\circ$后的位置,阴影与图形C阴影关于旋转中心中心对称。
(注:此处需根据实际图形A的阴影位置及变换要求在答题卡对应位置画出阴影,上述文字描述仅为辅助说明,实际作答以图形阴影为准。)
13. 亮点原创 将图中的一个三角形先横向平移 $m$ 格, 再纵向平移 $n$ 格, 就能与另一个三角形拼成一个四边形, 那么 $m + n$ 的值为 (
A.5 或 6 或 7
B.5 或 6
C.5 或 7
D.6 或 7
C
)A.5 或 6 或 7
B.5 或 6
C.5 或 7
D.6 或 7
答案:解:情况一:将上方三角形先向右平移1格,再向下平移4格,与下方三角形拼成四边形,此时$m=1$,$n=4$,$m + n=5$。
情况二:将上方三角形先向右平移3格,再向下平移4格,与下方三角形拼成四边形,此时$m=3$,$n=4$,$m + n=7$。
情况三:将下方三角形先向左平移1格,再向上平移4格,与上方三角形拼成四边形,此时$m=1$,$n=4$,$m + n=5$。
情况四:将下方三角形先向左平移3格,再向上平移4格,与上方三角形拼成四边形,此时$m=3$,$n=4$,$m + n=7$。
综上,$m + n$的值为5或7。
答案:C
情况二:将上方三角形先向右平移3格,再向下平移4格,与下方三角形拼成四边形,此时$m=3$,$n=4$,$m + n=7$。
情况三:将下方三角形先向左平移1格,再向上平移4格,与上方三角形拼成四边形,此时$m=1$,$n=4$,$m + n=5$。
情况四:将下方三角形先向左平移3格,再向上平移4格,与上方三角形拼成四边形,此时$m=3$,$n=4$,$m + n=7$。
综上,$m + n$的值为5或7。
答案:C
14. 在五行五列的方格棋盘上沿骰子的某条棱翻动骰子, 骰子在棋盘上只能向它所在格的左、右、前、后格翻动. 开始时骰子在 $3C$ 处, 如图 (1), 将骰子从 $3C$ 处翻动一次到 $3B$ 处, 骰子的形态如图 (2); 如果从 $3C$ 处开始翻动, 翻动两次后, 得到 $\vdots$ 朝上, 则此时骰子所在的位置是 ______.


答案:2B或4B
15. 在如图所示的网格中, 从边长为 6 的正方形左上角剪去一个边长为 2 的正方形, 得到六边形 $ABCDEF$, 该六边形按一定的方法可剪拼成一个正方形.
(1) 如图甲, 把六边形 $ABCDEF$ 沿 $EH, BG$ 剪成 (1)(2)(3) 三部分, 请在图甲中保持 (1) 不动, 画出拼成的正方形, 然后标出 (2)(3) 变动后的位置, 并指出 (2)(3) 分别属于哪一种变换;
(2) 在图乙中画出与图甲不同位置的两条裁剪线, 并画出将此六边形剪拼成的正方形.

(1) 如图甲, 把六边形 $ABCDEF$ 沿 $EH, BG$ 剪成 (1)(2)(3) 三部分, 请在图甲中保持 (1) 不动, 画出拼成的正方形, 然后标出 (2)(3) 变动后的位置, 并指出 (2)(3) 分别属于哪一种变换;
(2) 在图乙中画出与图甲不同位置的两条裁剪线, 并画出将此六边形剪拼成的正方形.

答案:
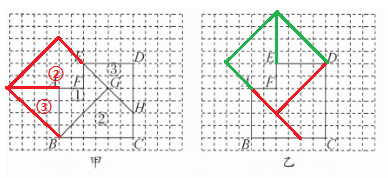
②③的变换是平移。

②③的变换是平移。