1. 如图,从学校A到书店B有①②③④四条路线,其中最短的路线是(
A.①
B.②
C.③
D.④
B
)A.①
B.②
C.③
D.④
答案：【解析】：
根据题目的描述和图示，我们可以看出这是一个关于直线、射线、线段概念的问题，需要找出从A到B的最短路线，根据“两点之间，线段最短”的原理，从A到B的最短路线应该是一条线段，观察图中的四条路线，我们可以看出只有路线②是一条从A到B的线段，因此，路线②是最短的。
【答案】：B
根据题目的描述和图示，我们可以看出这是一个关于直线、射线、线段概念的问题，需要找出从A到B的最短路线，根据“两点之间，线段最短”的原理，从A到B的最短路线应该是一条线段，观察图中的四条路线，我们可以看出只有路线②是一条从A到B的线段，因此，路线②是最短的。
【答案】：B
2. (教材P156练习1变式)在如图所示的梯形中,能用字母表示的线段共有(
A.12条
B.10条
C.8条
D.6条
B
)A.12条
B.10条
C.8条
D.6条
答案：【解析】：
本题考查直线、射线、线段的概念。
根据图中的梯形标记，我们可以数出以下线段：
梯形的四条边：$AB$，$BC$，$CD$，$DA$。
梯形的两条对角线：$AC$，$BD$。
由对角线交点 $E$ 引出的四条小线段：$AE$，$BE$，$CE$，$DE$。
一共 $4+ 2+ 4= 10$ 条线段。
【答案】：B。
本题考查直线、射线、线段的概念。
根据图中的梯形标记，我们可以数出以下线段：
梯形的四条边：$AB$，$BC$，$CD$，$DA$。
梯形的两条对角线：$AC$，$BD$。
由对角线交点 $E$ 引出的四条小线段：$AE$，$BE$，$CE$，$DE$。
一共 $4+ 2+ 4= 10$ 条线段。
【答案】：B。
3. 根据如图所示的图形解答下列问题：
(1)图中共有
(2)以O为端点的射线有
(3)图中共有
(1)图中共有
1
条直线,它们分别是直线AC
；(2)以O为端点的射线有
4
条,它们分别是射线OA、射线OB、射线OC、射线OD
；(3)图中共有
8
条线段.答案：(1)1；直线AC
(2)4；射线OA、射线OB、射线OC、射线OD
(3)8
(2)4；射线OA、射线OB、射线OC、射线OD
(3)8
4. 在植树造林活动中,为了使所栽的小树整齐排成一行,小刚建议先确定两个树坑的位置,然后就能确定同一行树坑的位置了,其理由是
两点确定一条直线
.答案：【解析】：
本题考查的是直线、射线、线段的基本性质。题目描述了植树造林活动中，为了使所栽的小树整齐排成一行，小刚建议先确定两个树坑的位置。这里涉及到的是几何学中关于直线的基本性质，即“两点确定一条直线”。通过先确定两个树坑的位置，就相当于确定了两个点，根据这两点可以确定一条直线，从而使得同一行的树坑都沿着这条直线排列，达到整齐的效果。
【答案】：
两点确定一条直线。
本题考查的是直线、射线、线段的基本性质。题目描述了植树造林活动中，为了使所栽的小树整齐排成一行，小刚建议先确定两个树坑的位置。这里涉及到的是几何学中关于直线的基本性质，即“两点确定一条直线”。通过先确定两个树坑的位置，就相当于确定了两个点，根据这两点可以确定一条直线，从而使得同一行的树坑都沿着这条直线排列，达到整齐的效果。
【答案】：
两点确定一条直线。
5. 亮点原创 如图,能用字母表示的以C为一个端点的线段的条数为m,能用字母表
示的以C为端点的射线的条数为n,则m-n= ______.(不添加其他字母)
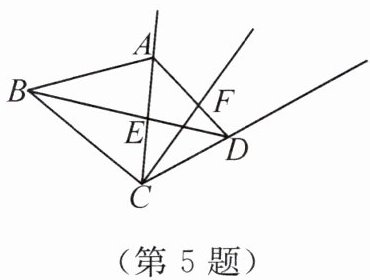
示的以C为端点的射线的条数为n,则m-n= ______.(不添加其他字母)
答案：答案略
6. 新素养 几何直观 如图,A,B,C,D四点不在同一条直线上.
(1)画射线DA；
(2)画直线CD；
(3)连接AB,BC；
(4)延长BC,交射线DA的反向延长线于点E.
(1)画射线DA；
(2)画直线CD；
(3)连接AB,BC；
(4)延长BC,交射线DA的反向延长线于点E.
答案：【解析】：
本题主要考查直线、射线和线段的基本概念以及它们的表示方法，同时涉及到点的连接和线的延长等操作。
(1) 画射线DA：根据射线的定义，射线有一个起点和一个方向。在这里，起点是点D，方向是沿着DA的方向。
(2) 画直线CD：直线是没有端点，可以向两端无限延伸的。在这里，我们画一条经过点C和点D的直线。
(3) 连接AB，BC：这是线段的操作，线段有两个端点。我们分别连接点A和点B，以及点B和点C，形成两条线段。
(4) 延长BC，交射线DA的反向延长线于点E：首先，我们延长线段BC；然后，我们考虑射线DA的反向延长线，即从点D出发，沿着与DA相反的方向延伸的射线。这条射线与延长后的BC相交于点E。
【答案】：
(1) 图略（从点D出发，沿DA方向画一条射线）
(2) 图略（经过点C和点D画一条直线）
(3) 图略（连接点A和点B，以及点B和点C，形成两条线段）
(4) 图略（延长线段BC，然后画出射线DA的反向延长线，两者相交于点E）
本题主要考查直线、射线和线段的基本概念以及它们的表示方法，同时涉及到点的连接和线的延长等操作。
(1) 画射线DA：根据射线的定义，射线有一个起点和一个方向。在这里，起点是点D，方向是沿着DA的方向。
(2) 画直线CD：直线是没有端点，可以向两端无限延伸的。在这里，我们画一条经过点C和点D的直线。
(3) 连接AB，BC：这是线段的操作，线段有两个端点。我们分别连接点A和点B，以及点B和点C，形成两条线段。
(4) 延长BC，交射线DA的反向延长线于点E：首先，我们延长线段BC；然后，我们考虑射线DA的反向延长线，即从点D出发，沿着与DA相反的方向延伸的射线。这条射线与延长后的BC相交于点E。
【答案】：
(1) 图略（从点D出发，沿DA方向画一条射线）
(2) 图略（经过点C和点D画一条直线）
(3) 图略（连接点A和点B，以及点B和点C，形成两条线段）
(4) 图略（延长线段BC，然后画出射线DA的反向延长线，两者相交于点E）
7. (2025·江苏南通期末)给出下列说法：
①直线MN和直线NM是同一条直线；
②射线AB和射线BA是同一条射线；
③线段PQ和线段QP是同一条线段；
④直线上一点把这条直线分成的两部分都是射线.其中正确的有(
A.1个
B.2个
C.3个
D.4个
①直线MN和直线NM是同一条直线；
②射线AB和射线BA是同一条射线；
③线段PQ和线段QP是同一条线段；
④直线上一点把这条直线分成的两部分都是射线.其中正确的有(
C
)A.1个
B.2个
C.3个
D.4个
答案：【解析】：
本题考查直线、射线、线段的概念。
① 直线MN和直线NM：根据直线的定义，直线不考虑起点和终点，只考虑方向上的无限延伸。因此，直线MN和直线NM表示的是同一条无限延伸的直线，只是标记的字母顺序不同。所以①正确。
② 射线AB和射线BA：射线有一个明确的起点和一个延伸的方向。射线AB表示起点为A，经过B并沿BA方向无限延伸；而射线BA表示起点为B，经过A并沿AB方向无限延伸。因此，它们不是同一条射线。所以②错误。
③ 线段PQ和线段QP：线段有两个端点，不考虑方向。线段PQ和线段QP表示的是同一段线段，只是端点的标记顺序不同。所以③正确。
④ 直线上一点把这条直线分成的两部分：根据射线的定义，射线有一个起点并沿一个方向无限延伸。因此，直线上的一点确实可以将直线分成两部分，每部分都是射线。所以④正确。
综上，正确的说法有3个。
【答案】：C.3个。
本题考查直线、射线、线段的概念。
① 直线MN和直线NM：根据直线的定义，直线不考虑起点和终点，只考虑方向上的无限延伸。因此，直线MN和直线NM表示的是同一条无限延伸的直线，只是标记的字母顺序不同。所以①正确。
② 射线AB和射线BA：射线有一个明确的起点和一个延伸的方向。射线AB表示起点为A，经过B并沿BA方向无限延伸；而射线BA表示起点为B，经过A并沿AB方向无限延伸。因此，它们不是同一条射线。所以②错误。
③ 线段PQ和线段QP：线段有两个端点，不考虑方向。线段PQ和线段QP表示的是同一段线段，只是端点的标记顺序不同。所以③正确。
④ 直线上一点把这条直线分成的两部分：根据射线的定义，射线有一个起点并沿一个方向无限延伸。因此，直线上的一点确实可以将直线分成两部分，每部分都是射线。所以④正确。
综上，正确的说法有3个。
【答案】：C.3个。
8. 如图,在直线l上有A,B,C,D四个点,则图中的线段共有(
A.3条
B.4条
C.6条
D.10条
C
)A.3条
B.4条
C.6条
D.10条
答案：【解析】：
本题主要考查了直线、射线、线段的概念以及计数的方法。
从A点出发，可以与B、C、D三点分别构成线段，即$AB$、$AC$、$AD$，共3条。
从B点出发（不再重复计算与A点构成的线段），可以与C、D两点分别构成线段，即$BC$、$BD$，共2条。
从C点出发（不再重复计算与A、B点构成的线段），只能与D点构成线段，即$CD$，共1条。
将上述所有线段数量相加，即得总线段数：$3 + 2 + 1 = 6$（条）。
【答案】：
C
本题主要考查了直线、射线、线段的概念以及计数的方法。
从A点出发，可以与B、C、D三点分别构成线段，即$AB$、$AC$、$AD$，共3条。
从B点出发（不再重复计算与A点构成的线段），可以与C、D两点分别构成线段，即$BC$、$BD$，共2条。
从C点出发（不再重复计算与A、B点构成的线段），只能与D点构成线段，即$CD$，共1条。
将上述所有线段数量相加，即得总线段数：$3 + 2 + 1 = 6$（条）。
【答案】：
C