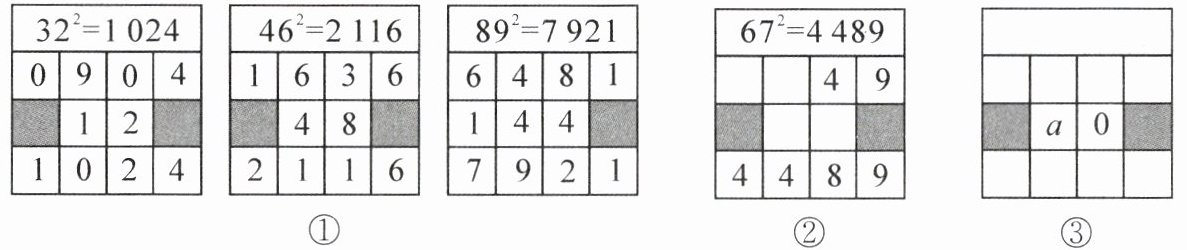
24. (5分)在求两位数的平方时,可以用“列竖式”的方法进行速算,求解过程如图①所示.
(1)仿照图①,在图②中补全$67^{2}$的“竖式”；
(2)仿照图①,用“列竖式”的方法计算一个两位数的平方,部分过程如图③所示.若这个两位数的个位数字为a(a不为0),则这个两位数为______.(用含a的代数式表示)
(1)仿照图①,在图②中补全$67^{2}$的“竖式”；
(2)仿照图①,用“列竖式”的方法计算一个两位数的平方,部分过程如图③所示.若这个两位数的个位数字为a(a不为0),则这个两位数为______.(用含a的代数式表示)
答案：
（1）如图所示: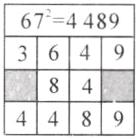
（2）50+a 解析:设这个两位数的十位数字为b,则2ab=10a,所以b=5,所以这个两位数为5×10+a=50+a.
（1）如图所示:
（2）50+a 解析:设这个两位数的十位数字为b,则2ab=10a,所以b=5,所以这个两位数为5×10+a=50+a.25. (6分)亮点原创新素养推理能力已知对任意正整数n,定义$f(n) = \frac{1}{1 + 2 + 3 + … + n}$.
(1)求$f(1) + f(2) + f(3) + … + f(2025)$的值；
(2)试说明：$\frac{3}{2} ＜ \frac{1}{1^{2}} + \frac{1}{2^{2}} + \frac{1}{3^{2}} + … + \frac{1}{2025^{2}} ＜ 2$.
(1)求$f(1) + f(2) + f(3) + … + f(2025)$的值；
(2)试说明：$\frac{3}{2} ＜ \frac{1}{1^{2}} + \frac{1}{2^{2}} + \frac{1}{3^{2}} + … + \frac{1}{2025^{2}} ＜ 2$.
答案：（1）因为$f(n)=\frac{1}{1+2+3+\cdots+n}=\frac{1}{\frac{1}{2}n(n+1)}=2\left(\frac{1}{n}-\frac{1}{n+1}\right)$,所以f(1)+f(2)+f(3)+…+f(2025)=$2×\left(1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\cdots+\frac{1}{2025}-\frac{1}{2026}\right)=2×\left(1-\frac{1}{2026}\right)=\frac{2025}{1013}$.（2）因为$\frac{1}{n^2}＞\frac{1}{n(n+1)}$,所以$\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+\cdots+\frac{1}{2025^2}＞1+\frac{1}{4}+\frac{1}{3×4}+\cdots+\frac{1}{2025×2026}=1+\frac{1}{4}+\frac{1}{3}-\frac{1}{4}+\cdots+\frac{1}{2025}-\frac{1}{2026}=\frac{5}{4}+\frac{1}{3}-\frac{1}{2026}=\frac{3}{2}+\frac{1}{12}-\frac{1}{2026}＞\frac{3}{2}$.因为$\frac{1}{n^2}＜\frac{1}{n(n-1)}$,所以$\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+\cdots+\frac{1}{2025^2}＜1+\frac{1}{1×2}+\frac{1}{2×3}+\cdots+\frac{1}{2024×2025}=1+1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\cdots+\frac{1}{2024}-\frac{1}{2025}=2-\frac{1}{2025}＜2$.综上所述,$\frac{3}{2}＜\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+\cdots+\frac{1}{2025^2}＜2$.