7. 已知$∠AOB= 30^{\circ }$,自$∠AOB$的顶点O引射线OC. 若$∠AOC:∠AOB= 4:3$,则$∠BOC$的度数是(
A.$10^{\circ }$
B.$40^{\circ }或30^{\circ }$
C.$70^{\circ }$
D.$10^{\circ }或70^{\circ }$
D
)A.$10^{\circ }$
B.$40^{\circ }或30^{\circ }$
C.$70^{\circ }$
D.$10^{\circ }或70^{\circ }$
答案:D
解析:
已知$\angle AOB = 30^{\circ}$,$\angle AOC:\angle AOB = 4:3$,则$\angle AOC=\frac{4}{3}\angle AOB=\frac{4}{3}×30^{\circ}=40^{\circ}$。
情况一:射线$OC$在$\angle AOB$内部,$\angle BOC=\angle AOC - \angle AOB=40^{\circ}-30^{\circ}=10^{\circ}$。
情况二:射线$OC$在$\angle AOB$外部,$\angle BOC=\angle AOC + \angle AOB=40^{\circ}+30^{\circ}=70^{\circ}$。
$\angle BOC$的度数是$10^{\circ}$或$70^{\circ}$。
D
情况一:射线$OC$在$\angle AOB$内部,$\angle BOC=\angle AOC - \angle AOB=40^{\circ}-30^{\circ}=10^{\circ}$。
情况二:射线$OC$在$\angle AOB$外部,$\angle BOC=\angle AOC + \angle AOB=40^{\circ}+30^{\circ}=70^{\circ}$。
$\angle BOC$的度数是$10^{\circ}$或$70^{\circ}$。
D
8. 如图,A,O,B三点在同一条直线上. 若$∠1$是锐角,则$∠1$的余角可表示为(
A.$\frac {1}{2}∠2-∠1$
B.$\frac {1}{2}(∠2-3∠1)$
C.$\frac {1}{2}(∠2-∠1)$
D.$\frac {1}{3}(∠1+∠2)$
C
)A.$\frac {1}{2}∠2-∠1$
B.$\frac {1}{2}(∠2-3∠1)$
C.$\frac {1}{2}(∠2-∠1)$
D.$\frac {1}{3}(∠1+∠2)$
答案:C
解析:
∵A,O,B三点共线,
∴∠1+∠2=180°,
∴∠2=180°-∠1,
∠1的余角为90°-∠1,
又∵90°=$\frac{1}{2}$(∠1+∠2),
∴90°-∠1=$\frac{1}{2}$(∠1+∠2)-∠1=$\frac{1}{2}$(∠2-∠1)。
C
∴∠1+∠2=180°,
∴∠2=180°-∠1,
∠1的余角为90°-∠1,
又∵90°=$\frac{1}{2}$(∠1+∠2),
∴90°-∠1=$\frac{1}{2}$(∠1+∠2)-∠1=$\frac{1}{2}$(∠2-∠1)。
C
9. (2025·江苏南京期末)已知D为线段AC的中点,B为直线AC上的一点,且$BC= \frac {1}{2}AB$. 若$BD= 1$,则线段AC的长为( )
A.$\frac {2}{3}$
B.$\frac {3}{2}$
C.6或$\frac {2}{3}$
D.6或$\frac {3}{2}$
A.$\frac {2}{3}$
B.$\frac {3}{2}$
C.6或$\frac {2}{3}$
D.6或$\frac {3}{2}$
答案:
C 解析:设 BC=x. 因为 BC=$\frac{1}{2}$AB,所以 AB=2BC=2x. 因为 BD=1,所以分类讨论如下:① 如图①,当点 B 在线段 AC 上时,AC=AB+BC=3x. 因为 D 为线段 AC 的中点,所以 AD=$\frac{1}{2}$AC=1.5x,所以 BD=AB-AD=0.5x,所以 0.5x=1,解得 x=2,所以 AC=6;② 如图②,当点 B 在线段 AC 的延长线上时,AC=AB-BC=x. 因为 D 为线段 AC 的中点,所以 CD=$\frac{1}{2}$AC=0.5x,所以 BD=BC+CD=1.5x,所以 1.5x=1,解得 x=$\frac{2}{3}$,所以 AC=$\frac{2}{3}$. 综上所述,线段 AC 的长为 6 或$\frac{2}{3}$.
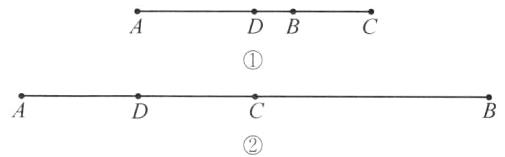
C 解析:设 BC=x. 因为 BC=$\frac{1}{2}$AB,所以 AB=2BC=2x. 因为 BD=1,所以分类讨论如下:① 如图①,当点 B 在线段 AC 上时,AC=AB+BC=3x. 因为 D 为线段 AC 的中点,所以 AD=$\frac{1}{2}$AC=1.5x,所以 BD=AB-AD=0.5x,所以 0.5x=1,解得 x=2,所以 AC=6;② 如图②,当点 B 在线段 AC 的延长线上时,AC=AB-BC=x. 因为 D 为线段 AC 的中点,所以 CD=$\frac{1}{2}$AC=0.5x,所以 BD=BC+CD=1.5x,所以 1.5x=1,解得 x=$\frac{2}{3}$,所以 AC=$\frac{2}{3}$. 综上所述,线段 AC 的长为 6 或$\frac{2}{3}$.

10. 新素养 推理能力 如图,在长方形ABCD中,$AB:BC= 2:1,AB= 12cm$,点P从点A出发,沿边AB以2 cm/s的速度向点B运动,点Q从点D出发,沿边DA以1 cm/s的速度向点A运动. 假设P,Q两点同时出发,运动时间为$ts(0\lt t\lt 6)$. 在整个运动过程中,给出下列结论:① 图中共有11条线段;② 图中共有19个小于平角的角;③ 当$t= 2$时,$PB:BC= 4:3$;④ 四边形QAPC的面积为$36cm^{2}$. 其中正确的有(
A.1个
B.2个
C.3个
D.4个
D
)A.1个
B.2个
C.3个
D.4个
答案:D 解析:题图中线段有 AP,AB,PB,BC,CD,DQ,DA,AQ,PC,CQ,PQ,共 11 条,故①正确;图中小于平角的角有∠A,∠B,∠BCD,∠D,∠APQ,∠BPC,∠CPQ,∠APC,∠BPQ,∠BCP,∠PCQ,∠QCD,∠BCQ,∠PCD,∠CQD,∠PQC,∠AQP,∠AQC,∠PQD,共 19 个,故②正确;当 t=2 时,AP=2×2=4(cm). 因为 AB=12 cm,所以 PB=AB-AP=8 cm. 因为 AB:BC=2:1,所以 BC=$\frac{1}{2}$AB=6 cm,所以 PB:BC=4:3,故③正确;因为 PB=AB-AP=(12-2t)cm,DQ=t cm,所以四边形 QAPC 的面积为 12×6-$\frac{1}{2}$(12-2t)×6-$\frac{1}{2}$×12×t=72-36+6t-6t=36(cm²),故④正确. 综上所述,其中正确的结论有 4 个.
11. (2023·四川乐山)如图,点O在直线AB上,OD是$∠BOC$的平分线. 若$∠AOC= 140^{\circ }$,则$∠BOD$的度数为______.
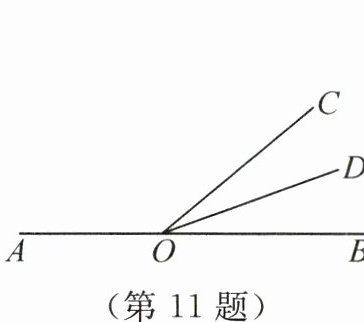

20°
答案:20°
解析:
∵点O在直线AB上,
∴∠AOC + ∠BOC = 180°,
∵∠AOC = 140°,
∴∠BOC = 180° - ∠AOC = 180° - 140° = 40°,
∵OD是∠BOC的平分线,
∴∠BOD = $\frac{1}{2}$∠BOC = $\frac{1}{2}$×40° = 20°。
20°
∴∠AOC + ∠BOC = 180°,
∵∠AOC = 140°,
∴∠BOC = 180° - ∠AOC = 180° - 140° = 40°,
∵OD是∠BOC的平分线,
∴∠BOD = $\frac{1}{2}$∠BOC = $\frac{1}{2}$×40° = 20°。
20°
12. 如图,$OA⊥OB,∠AOD= \frac {1}{2}∠COD,∠BOC= 3∠AOD$,则$∠COD=$
30°
.答案:30°
解析:
设$∠AOD = x$,则$∠COD = 2x$,$∠BOC = 3x$。
因为$OA⊥OB$,所以$∠AOB = 90^{\circ}$。
由图可知$∠BOC + ∠COD + ∠AOD = ∠AOB$,即$3x + 2x + x = 90^{\circ}$,解得$6x = 90^{\circ}$,$x = 15^{\circ}$。
所以$∠COD = 2x = 2×15^{\circ} = 30^{\circ}$。
$30^{\circ}$
因为$OA⊥OB$,所以$∠AOB = 90^{\circ}$。
由图可知$∠BOC + ∠COD + ∠AOD = ∠AOB$,即$3x + 2x + x = 90^{\circ}$,解得$6x = 90^{\circ}$,$x = 15^{\circ}$。
所以$∠COD = 2x = 2×15^{\circ} = 30^{\circ}$。
$30^{\circ}$
13. (2023·内蒙古通辽)将一副三角板如图所示放置,其中$AB// DE$,则$∠CDF= $______.


105°
答案:105°
解析:
∵AB//DE,
∴∠ADE=∠A=90°,
∵∠EDF=45°,
∴∠CDF=180°-∠ADE-∠EDF=180°-90°-45°=45°。
105°
∴∠ADE=∠A=90°,
∵∠EDF=45°,
∴∠CDF=180°-∠ADE-∠EDF=180°-90°-45°=45°。
105°
14. 若一个角的补角是这个角余角的4倍,则这个角的度数是
60°
.答案:60°
解析:
设这个角的度数为$x$。
这个角的补角为$180^\circ - x$,余角为$90^\circ - x$。
由题意得:$180^\circ - x = 4(90^\circ - x)$
$180^\circ - x = 360^\circ - 4x$
$-x + 4x = 360^\circ - 180^\circ$
$3x = 180^\circ$
$x = 60^\circ$
60°
这个角的补角为$180^\circ - x$,余角为$90^\circ - x$。
由题意得:$180^\circ - x = 4(90^\circ - x)$
$180^\circ - x = 360^\circ - 4x$
$-x + 4x = 360^\circ - 180^\circ$
$3x = 180^\circ$
$x = 60^\circ$
60°