15. 已知线段$AB= 8$,C是AB的中点,点D在直线CB上,且$BD= 1.5$,则线段CD的长为
2.5 或 5.5
.答案:2.5 或 5.5
解析:
∵AB=8,C是AB的中点,
∴CB=$\frac{1}{2}$AB=4。
当点D在点B右侧时,CD=CB+BD=4+1.5=5.5;
当点D在点B左侧时,CD=CB-BD=4-1.5=2.5。
2.5或5.5
∴CB=$\frac{1}{2}$AB=4。
当点D在点B右侧时,CD=CB+BD=4+1.5=5.5;
当点D在点B左侧时,CD=CB-BD=4-1.5=2.5。
2.5或5.5
16. 一副直角三角板按如图所示的方式放置,将三角板ADE绕点A逆时针旋转$∠α(0^{\circ }\lt ∠α\lt 90^{\circ })$,使得三角板ADE的一边所在的直线与BC垂直,则$∠α$的度数为______

15°或 60°
.
答案:15°或 60°
17. (2025·江苏苏州期末)如图,已知A是射线BE上一点,过点A画$AC⊥BF$,垂足为C,过点C画$CD⊥BE$,垂足为D. 给出下列结论:①$∠1是∠ACD$的余角;② 图中互余的角共有3对;③ 图中$∠1的补角只有∠DCF$;④ 图中与$∠ADC$互补的角共有3个. 其中正确的是______.(填序号)


①④
答案:①④ 解析:因为 AC⊥BF,所以∠ACB=∠ACF=90°,所以∠ACD+∠1=90°,所以∠1 是∠ACD 的余角,故①正确;因为 CD⊥BE,所以∠ADC=∠BDC=90°,所以∠DAC+∠ACD=180°-∠ADC=90°,∠B+∠1=180°-∠BDC=90°. 因为∠ACB=90°,所以∠1+∠ACD=90°,∠B+∠BAC=180°-∠ACB=90°,所以题图中互余的角共有 4 对,故②错误;因为∠1+∠DCF=180°,所以∠DCF 是∠1 的补角. 因为∠1+∠ACD=90°,∠DAC+∠ACD=90°,所以∠1=∠DAC. 因为∠DAC+∠CAE=180°,所以∠1+∠CAE=180°,所以∠CAE 也是∠1 的补角,故③错误;因为∠ADC=90°,∠BDC=∠ACB=∠ACF=90°,所以题图中与∠ADC 互补的角共有 3 个,故④正确.
18. 亮点原创 如图,3条直线两两相交最多有3个交点,4条直线两两相交最多有6个交点,…,按照这样的规律,则2025条直线两两相交最多有
2049300
个交点.答案:2049300 解析:因为 3 条直线两两相交最多有 1+2=3(个)交点,4 条直线两两相交最多有 1+2+3=6(个)交点,…,所以按照这样的规律,2025 条直线两两相交最多有 1+2+3+…+2024=$\frac{(1+2024)×2024}{2}$=2049300(个)交点.
解析:
1+2+3+…+2024=$\frac{(1+2024)×2024}{2}$=2049300
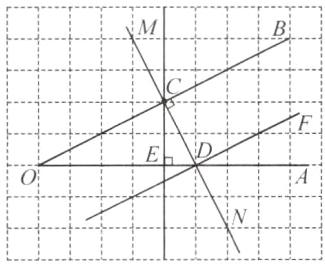
19. (6分)新素养 几何直观 在如图所示的方格纸中,C是$∠AOB$的边OB上的一点,按下列要求画图并解答问题:
(1)过点C画OB的垂线,交OA于点D. 该垂线经过的格点有哪些?请在图中标出该垂线所经过的格点;(网格线的交点称为格点)
(2)过点C画OA的垂线,垂足为E.
① 线段CE的长是点C到直线______的距离,线段______的长是点D到直线OB的距离;
② 因为直线外一点与直线上各点连接的所有线段中,垂线段最短,所以CD,CE,OD,OC这四条线段长度的大小关系是______;(用“<”号连接)
(3)过点D画直线$DF// OB$. 若$∠AOB= x^{\circ }$,则$∠ADC= $______.(用含x的式子表示)

(1)过点C画OB的垂线,交OA于点D. 该垂线经过的格点有哪些?请在图中标出该垂线所经过的格点;(网格线的交点称为格点)
(2)过点C画OA的垂线,垂足为E.
① 线段CE的长是点C到直线______的距离,线段______的长是点D到直线OB的距离;
② 因为直线外一点与直线上各点连接的所有线段中,垂线段最短,所以CD,CE,OD,OC这四条线段长度的大小关系是______;(用“<”号连接)
(3)过点D画直线$DF// OB$. 若$∠AOB= x^{\circ }$,则$∠ADC= $______.(用含x的式子表示)

答案:
(1)如图,该垂线经过的格点有点 C,D,M,N.
(2)如图所示.
① OA CD ② CE<CD<OC<OD
(3)如图所示. (90+x)°
(1)如图,该垂线经过的格点有点 C,D,M,N.

(2)如图所示.
① OA CD ② CE<CD<OC<OD
(3)如图所示. (90+x)°