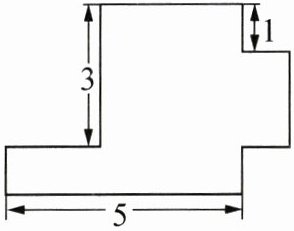
17. (2025·江苏扬州期末)如图是一个无盖长方体盒子的表面展开图(重叠部分不计),根据图中数据可知,该无盖长方体盒子的容积为______.(不考虑盒子厚度)

6
答案:6 解析:由题图可知,该无盖长方体盒子的高为1,宽为$3-1=2$,长为$5-2=3$,所以该无盖长方体盒子的容积为$3×2×1=6$.
解析:
由展开图可知,长方体盒子的高为$1$,宽为$3 - 1=2$,长为$5 - 2=3$,容积为$3×2×1 = 6$。
6
6
18. 亮点原创对于任意正有理数a,规定$f(a)= \frac{2a}{a+1}$,例如:$f(2)= \frac{2×2}{2+1}= \frac{4}{3},f(\frac{1}{2})= \frac{2×\frac{1}{2}}{\frac{1}{2}+1}= \frac{2}{3},…$.利用以上规律计算:$f(\frac{1}{2025})+f(\frac{1}{2024})+…+f(\frac{1}{3})+f(\frac{1}{2})+f(1)+f(2)+f(3)+…+f(2024)+f(2025)= $
4049
.答案:4049 解析:由题意,得原式$=2×\left(\frac {1}{2026}+\frac {1}{2025}+\cdots +\frac {1}{4}+\frac {1}{3}+\frac {1}{2}+\frac {2}{3}+\frac {3}{4}+\cdots +\frac {2024}{2025}+\frac {2025}{2026}\right)=2×\left[\left(\frac {1}{2026}+\frac {2025}{2026}\right)+\left(\frac {1}{2025}+\frac {2024}{2025}\right)+\cdots +\left(\frac {1}{4}+\frac {3}{4}\right)+\left(\frac {1}{3}+\frac {2}{3}\right)+\frac {1}{2}\right]=2×\left(1+1+\cdots +1+1+\frac {1}{2}\right)=2×\left(1×2024+\frac {1}{2}\right)=4049$.
解析:
由题意,$f(a)=\frac{2a}{a+1}$,则:
$f\left(\frac{1}{n}\right)=\frac{2×\frac{1}{n}}{\frac{1}{n}+1}=\frac{2}{n+1}$,$f(n)=\frac{2n}{n+1}$($n$为正整数)。
原式$=f\left(\frac{1}{2025}\right)+f\left(\frac{1}{2024}\right)+\cdots+f\left(\frac{1}{2}\right)+f(1)+f(2)+\cdots+f(2025)$
$=\sum_{n=1}^{2025}f\left(\frac{1}{n}\right)+\sum_{n=2}^{2025}f(n)$
$=\sum_{n=1}^{2025}\frac{2}{n+1}+\sum_{n=2}^{2025}\frac{2n}{n+1}$
$=2\left[\sum_{n=1}^{2025}\frac{1}{n+1}+\sum_{n=2}^{2025}\frac{n}{n+1}\right]$
$=2\left[\frac{1}{2}+\sum_{n=2}^{2025}\left(\frac{1}{n+1}+\frac{n}{n+1}\right)\right]$
$=2\left[\frac{1}{2}+\sum_{n=2}^{2025}1\right]$
$=2\left[\frac{1}{2}+(2025 - 1)×1\right]$
$=2\left[\frac{1}{2}+2024\right]$
$=2×\frac{4049}{2}=4049$
4049
$f\left(\frac{1}{n}\right)=\frac{2×\frac{1}{n}}{\frac{1}{n}+1}=\frac{2}{n+1}$,$f(n)=\frac{2n}{n+1}$($n$为正整数)。
原式$=f\left(\frac{1}{2025}\right)+f\left(\frac{1}{2024}\right)+\cdots+f\left(\frac{1}{2}\right)+f(1)+f(2)+\cdots+f(2025)$
$=\sum_{n=1}^{2025}f\left(\frac{1}{n}\right)+\sum_{n=2}^{2025}f(n)$
$=\sum_{n=1}^{2025}\frac{2}{n+1}+\sum_{n=2}^{2025}\frac{2n}{n+1}$
$=2\left[\sum_{n=1}^{2025}\frac{1}{n+1}+\sum_{n=2}^{2025}\frac{n}{n+1}\right]$
$=2\left[\frac{1}{2}+\sum_{n=2}^{2025}\left(\frac{1}{n+1}+\frac{n}{n+1}\right)\right]$
$=2\left[\frac{1}{2}+\sum_{n=2}^{2025}1\right]$
$=2\left[\frac{1}{2}+(2025 - 1)×1\right]$
$=2\left[\frac{1}{2}+2024\right]$
$=2×\frac{4049}{2}=4049$
4049
19. (6分)新素养 运算能力
(1)计算:$(\frac{5}{6}-\frac{4}{9})+|\frac{1}{6}-\frac{2}{9}|-(-\frac{1}{2})$;
(2)计算:$(-2)^{4}-[-1+(-\frac{1}{2})]×(-3^{2}+2)$;
(3)先化简,再求值:$x-2(\frac{1}{4}x-\frac{1}{3}y^{2})+(-\frac{3}{2}x+\frac{1}{3}y^{2})$,其中x,y满足$|x-\frac{3}{2}|+(y+2)^{2}= 0$.
(1)计算:$(\frac{5}{6}-\frac{4}{9})+|\frac{1}{6}-\frac{2}{9}|-(-\frac{1}{2})$;
(2)计算:$(-2)^{4}-[-1+(-\frac{1}{2})]×(-3^{2}+2)$;
(3)先化简,再求值:$x-2(\frac{1}{4}x-\frac{1}{3}y^{2})+(-\frac{3}{2}x+\frac{1}{3}y^{2})$,其中x,y满足$|x-\frac{3}{2}|+(y+2)^{2}= 0$.
答案:(1)原式$=\frac {7}{18}+\frac {1}{18}+\frac {1}{2}=\frac {17}{18}$.(2)原式$=16-\left(-\frac {3}{2}\right)×(-9+2)=16-\frac {3}{2}×7=\frac {11}{2}$.(3)原式$=x-\frac {x}{2}+\frac {2}{3}y^{2}-\frac {3}{2}x+\frac {1}{3}y^{2}=y^{2}-x$.因为$|x-\frac {3}{2}|+(y+2)^{2}=0$,所以$x-\frac {3}{2}=0$,$y+2=0$,所以$x=\frac {3}{2}$,$y=-2$,所以原式$=(-2)^{2}-\frac {3}{2}=\frac {5}{2}$.
解析:
(1)原式$=\frac{5}{6}-\frac{4}{9}+\left|\frac{1}{6}-\frac{2}{9}\right|+\frac{1}{2}$
$=\frac{15}{18}-\frac{8}{18}+\left|\frac{3}{18}-\frac{4}{18}\right|+\frac{9}{18}$
$=\frac{7}{18}+\frac{1}{18}+\frac{9}{18}$
$=\frac{17}{18}$
(2)原式$=16-\left(-\frac{3}{2}\right)×(-9 + 2)$
$=16-\left(-\frac{3}{2}\right)×(-7)$
$=16-\frac{21}{2}$
$=\frac{32}{2}-\frac{21}{2}$
$=\frac{11}{2}$
(3)原式$=x-\frac{1}{2}x+\frac{2}{3}y^{2}-\frac{3}{2}x+\frac{1}{3}y^{2}$
$=(x-\frac{1}{2}x-\frac{3}{2}x) + (\frac{2}{3}y^{2}+\frac{1}{3}y^{2})$
$=-x + y^{2}$
$=y^{2}-x$
因为$|x-\frac{3}{2}|+(y + 2)^{2}=0$,所以$x-\frac{3}{2}=0$,$y + 2=0$,即$x=\frac{3}{2}$,$y=-2$
原式$=(-2)^{2}-\frac{3}{2}$
$=4-\frac{3}{2}$
$=\frac{5}{2}$
$=\frac{15}{18}-\frac{8}{18}+\left|\frac{3}{18}-\frac{4}{18}\right|+\frac{9}{18}$
$=\frac{7}{18}+\frac{1}{18}+\frac{9}{18}$
$=\frac{17}{18}$
(2)原式$=16-\left(-\frac{3}{2}\right)×(-9 + 2)$
$=16-\left(-\frac{3}{2}\right)×(-7)$
$=16-\frac{21}{2}$
$=\frac{32}{2}-\frac{21}{2}$
$=\frac{11}{2}$
(3)原式$=x-\frac{1}{2}x+\frac{2}{3}y^{2}-\frac{3}{2}x+\frac{1}{3}y^{2}$
$=(x-\frac{1}{2}x-\frac{3}{2}x) + (\frac{2}{3}y^{2}+\frac{1}{3}y^{2})$
$=-x + y^{2}$
$=y^{2}-x$
因为$|x-\frac{3}{2}|+(y + 2)^{2}=0$,所以$x-\frac{3}{2}=0$,$y + 2=0$,即$x=\frac{3}{2}$,$y=-2$
原式$=(-2)^{2}-\frac{3}{2}$
$=4-\frac{3}{2}$
$=\frac{5}{2}$