9. (3分) 已知$|x|= 3$,$y^{2}= 4$,且$xy<0$,则$x-y$的值为 (
A.5
B.$-1$
C.1或$-1$
D.$-5$或5
D
)A.5
B.$-1$
C.1或$-1$
D.$-5$或5
答案:D
解析:
因为$|x| = 3$,所以$x = 3$或$x=-3$;
因为$y^{2}=4$,所以$y = 2$或$y=-2$;
又因为$xy<0$,
当$x = 3$时,$y=-2$,则$x - y=3-(-2)=5$;
当$x=-3$时,$y = 2$,则$x - y=-3 - 2=-5$;
综上,$x - y$的值为$-5$或$5$。
D
因为$y^{2}=4$,所以$y = 2$或$y=-2$;
又因为$xy<0$,
当$x = 3$时,$y=-2$,则$x - y=3-(-2)=5$;
当$x=-3$时,$y = 2$,则$x - y=-3 - 2=-5$;
综上,$x - y$的值为$-5$或$5$。
D
10. (3分) 新素养 几何直观 已知$a$,$b$,$c$三个数在数轴上的位置如图所示,给出下列结论:①$abc<0$;②$-c>a>-b$;③$a+c>0$;④$|a-c|+|b-a|= |b-c|$. 其中正确的个数是 (
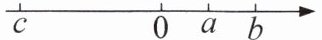
A.4
B.3
C.2
D.1
B
)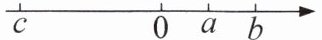
A.4
B.3
C.2
D.1
答案:B
解析:
由数轴知$c<0<a<b$,且$|c|>|b|>|a|$。
①$abc<0$,正确;
②$-c>|b|>a$,$-b<0$,则$-c>a>-b$,正确;
③$a+c<0$,错误;
④$|a-c|+|b-a|=(a-c)+(b-a)=b-c=|b-c|$,正确。
正确的有①②④,共3个。
B
①$abc<0$,正确;
②$-c>|b|>a$,$-b<0$,则$-c>a>-b$,正确;
③$a+c<0$,错误;
④$|a-c|+|b-a|=(a-c)+(b-a)=b-c=|b-c|$,正确。
正确的有①②④,共3个。
B
11. (3分) 新素养 抽象能力 定义新运算:用“$÷$”连接$n个相同非零有理数a$所构成的运算叫作除方,记作$a^{\enclose{circle} {n}}$. 比如$2^{③}= 2÷ 2÷ 2$读作“2的圈3次方”,$(-3)^{\enclose{circle} {4}}= (-3)÷ (-3)÷ (-3)÷ (-3)$,读作“$-3$的圈4次方”. 下面说法不正确的是 (
A.任意非零数的圈3次方都等于它的倒数
B.圈$n$次方等于它本身的数是1或$-1$($n$为任意正整数)
C.互为相反数的两个数的圈$n$次方不一定互为相反数
D.互为倒数的两个数的圈$n$次方互为倒数
B
)A.任意非零数的圈3次方都等于它的倒数
B.圈$n$次方等于它本身的数是1或$-1$($n$为任意正整数)
C.互为相反数的两个数的圈$n$次方不一定互为相反数
D.互为倒数的两个数的圈$n$次方互为倒数
答案:B
解析:
A. $a^{\enclose{circle}{3}}=a÷ a÷ a=1÷ a=\frac{1}{a}$,正确。
B. 当$n=1$时,$a^{\enclose{circle}{1}}=a$,任意非零数均满足,错误。
C. 如$2^{\enclose{circle}{4}}=2÷2÷2÷2=\frac{1}{4}$,$(-2)^{\enclose{circle}{4}}=(-2)÷(-2)÷(-2)÷(-2)=\frac{1}{4}$,不互为相反数,正确。
D. 设$a$与$\frac{1}{a}$互为倒数,$a^{\enclose{circle}{n}}=a÷ a÷\cdots÷ a=\frac{1}{a^{n-2}}$,$(\frac{1}{a})^{\enclose{circle}{n}}=\frac{1}{a}÷\frac{1}{a}÷\cdots÷\frac{1}{a}=a^{n-2}$,二者互为倒数,正确。
B
B. 当$n=1$时,$a^{\enclose{circle}{1}}=a$,任意非零数均满足,错误。
C. 如$2^{\enclose{circle}{4}}=2÷2÷2÷2=\frac{1}{4}$,$(-2)^{\enclose{circle}{4}}=(-2)÷(-2)÷(-2)÷(-2)=\frac{1}{4}$,不互为相反数,正确。
D. 设$a$与$\frac{1}{a}$互为倒数,$a^{\enclose{circle}{n}}=a÷ a÷\cdots÷ a=\frac{1}{a^{n-2}}$,$(\frac{1}{a})^{\enclose{circle}{n}}=\frac{1}{a}÷\frac{1}{a}÷\cdots÷\frac{1}{a}=a^{n-2}$,二者互为倒数,正确。
B
12. (3分) 体育课上的口令:立正,向右转,向后转,向左转之间可以相加. 连接执行两个口令就把这两个口令加起来. 例如:向右转$+向左转= $立正;向左转$+向后转= $向右转. 如果用0,1,2,3分别代表立正,向右转,向后转,向左转,那么可以用如图所示的加法表来表示,在表中填了部分的数值和代表数值的字母. 下列对于字母$a$,$b$,$c$,$d$的值,说法错误的是 (

A.$a= 0$
B.$b= 1$
C.$c= 2$
D.$d= 3$
C
)
A.$a= 0$
B.$b= 1$
C.$c= 2$
D.$d= 3$
答案:C 解析:由题意,得a=0,b=1,c=1,d=3.
13. (3分) 同学们都熟悉“幻方”游戏,现将“幻方”游戏稍作改进变成“幻圆”游戏,将$-2$,4,$-6$,8,$-10$,12,$-14$,16分别填入图中的圆圈内,使横、竖以及内外两个正方形顶点处圈内4个数字之和都相等,则$a+b$的值为 (
A.$-6或-12$
B.$-2或-8$
C.2或$-2$
D.2或$-16$
A
)A.$-6或-12$
B.$-2或-8$
C.2或$-2$
D.2或$-16$
答案:A 解析:设左、右两个空白处的数分别为m,n.因为-2+4-6+8-10+12-14+16=8,所以横、竖以及内外两个正方形顶点处圈内4个数字之和都为8÷2=4,所以a=4-(-14+12+16)=-10,所以m=4-(12+8-10)=-6,所以b=4,n=-2或b=-2,n=4,所以a+b=-10+4=-6或-10-2=-12.
14. (3分) 已知两个多项式$A= x^{2}+2x+2$,$B= x^{2}-2x+2$,给出下列结论:①若$A+B= 12$,则$x= \pm 2$;②若$A+B+ax^{2}-bx的值与x$的值无关,则$a+b= -2$;③若$|A-B-8|+|A-B+4|= 12$,则$-1\leqslant x\leqslant 2$;④若$y$是整数,且满足等式$(m-1)y= A+B-2x^{2}$,则符合条件的非负整数$m$有3个. 其中正确的有 (
A.1个
B.2个
C.3个
D.4个
C
)A.1个
B.2个
C.3个
D.4个
答案:C 解析:因为A=x²+2x+2,B=x²-2x+2,所以A+B=2x²+4.若A+B=12,则2x²+4=12,所以x²=4.因为(±2)²=4,所以x=±2,故①正确;A+B+ax²-bx=2x²+4+ax²-bx=(a+2)x²-bx+4.若A+B+ax²-bx的值与x的值无关,则a+2=0且b=0,所以a=-2,所以a+b=-2,故②正确;因为A-B=4x,所以若|A-B-8|+|A-B+4|=12,则|4x-8|+|4x+4|=12,所以|x-2|+|x+1|=3,当且仅当-1≤x≤2时等式成立,故③正确;由(m-1)y=A+B-2x²,得(m-1)y=2x²+4-2x²,即(m-1)y=4.因为y是整数,且m是非负整数,所以m-1=-1或1或2或4,所以m=0或2或3或5,有4个,故③错误.综上所述,其中正确的结论有3个.