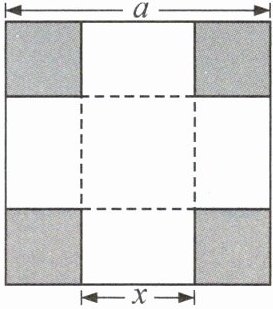
4.(10分)新趋势 综合实践 某数学兴趣小组开展了“制作一个尽可能大的无盖长方体纸盒”的实践活动,他们利用边长为$a\mathrm{c}\mathrm{m}$的正方形纸板制作出一个无盖的长方体纸盒(纸板厚度及接缝处忽略不计).具体方法如下:如图,先在纸板四角剪去四个同样大小的小正方形,再沿虚线折合起来,这样可制作一个无盖的长方体纸盒.设底面边长为$x(x\lt a)\mathrm{c}\mathrm{m}$.
(1)这个纸盒的底面积是______$\mathrm{c}{\mathrm{m}}^{\mathrm{2}}$,高是______$\mathrm{c}\mathrm{m}$;(用含$a,x$的代数式表示)
(2)$x$的部分取值及相应的纸盒容积如下表所示,根据表格完成填空;
| $x/\mathrm{c}\mathrm{m}$ | 2 | 4 | 6 | 8 |
| 纸盒容积$V/\mathrm{c}{\mathrm{m}}^{\mathrm{3}}$ | ______ | 48 | ______ | ______ |
(3)若纸盒的容积大于上表中的4个容积值,则$x$的值可以是______.(写一个即可)
(1)
(2)
(3)
(1)这个纸盒的底面积是______$\mathrm{c}{\mathrm{m}}^{\mathrm{2}}$,高是______$\mathrm{c}\mathrm{m}$;(用含$a,x$的代数式表示)
(2)$x$的部分取值及相应的纸盒容积如下表所示,根据表格完成填空;
| $x/\mathrm{c}\mathrm{m}$ | 2 | 4 | 6 | 8 |
| 纸盒容积$V/\mathrm{c}{\mathrm{m}}^{\mathrm{3}}$ | ______ | 48 | ______ | ______ |
(3)若纸盒的容积大于上表中的4个容积值,则$x$的值可以是______.(写一个即可)

(1)
$x^{2}$
$\frac{a-x}{2}$
(2)
16
72
64
(3)
7
答案:(1)$x^{2}\frac{a-x}{2}$
(2)16 72 64 解析:由(1),得$V=x^{2}\cdot\frac{a-x}{2}$.因为当$x=4$时,$V=48$,所以$4^{2}\cdot\frac{a-4}{2}=48$,解得$a=10$,所以$V=x^{2}\cdot\frac{10-x}{2}$.当$x=2$时,$V=2^{2}×\frac{10-8}{2}=16$;当$x=6$时,$V=6^{2}×\frac{10-6}{2}=72$;当$x=8$时,$V=8^{2}×\frac{10-8}{2}=64$.
(3)7(答案不唯一)
(2)16 72 64 解析:由(1),得$V=x^{2}\cdot\frac{a-x}{2}$.因为当$x=4$时,$V=48$,所以$4^{2}\cdot\frac{a-4}{2}=48$,解得$a=10$,所以$V=x^{2}\cdot\frac{10-x}{2}$.当$x=2$时,$V=2^{2}×\frac{10-8}{2}=16$;当$x=6$时,$V=6^{2}×\frac{10-6}{2}=72$;当$x=8$时,$V=8^{2}×\frac{10-8}{2}=64$.
(3)7(答案不唯一)
5.(2025·江苏淮安期末·12分)
【阅读】
如图,点$A,B在数轴上分别表示数a,b$,则$A,B两点之间的距离可以表示为AB= |a-b|$.

【理解】
(1)数轴上表示2和5的两点之间的距离是
(2)数轴上表示$x$和-1的两点$M,N$之间的距离是
【运用】
(3)当代数式$|x+1|+|x-2|$取最小值时,$x$的取值范围是
(4)当代数式$|x+1|+|x-2|+|x-4|$取最小值时,$x$的值是
【提升】
(5)$A,B,C,D,E$五名同学按顺时针方向围成一个圆,他们手中的卡片张数分别为12,6,9,3,10.现在为使每名同学手中的卡片数相等,安排每名同学调几张卡片给相邻同学(可以从相邻同学调进或调出给相邻同学).要使调动的卡片总张数最少,应做怎样的调动安排?最少调动几张?
【阅读】
如图,点$A,B在数轴上分别表示数a,b$,则$A,B两点之间的距离可以表示为AB= |a-b|$.

【理解】
(1)数轴上表示2和5的两点之间的距离是
3
,数轴上表示1和-3的两点之间的距离是4
;(2)数轴上表示$x$和-1的两点$M,N$之间的距离是
|x+1|
;如果点$M与点N$之间的距离是2,那么$x$的值是1或-3
;【运用】
(3)当代数式$|x+1|+|x-2|$取最小值时,$x$的取值范围是
$-1\leqslant x\leqslant2$
;(4)当代数式$|x+1|+|x-2|+|x-4|$取最小值时,$x$的值是
2
;【提升】
(5)$A,B,C,D,E$五名同学按顺时针方向围成一个圆,他们手中的卡片张数分别为12,6,9,3,10.现在为使每名同学手中的卡片数相等,安排每名同学调几张卡片给相邻同学(可以从相邻同学调进或调出给相邻同学).要使调动的卡片总张数最少,应做怎样的调动安排?最少调动几张?
设A,B,C,D,E五名同学按顺时针方向依次调给相邻同学$x_{1},x_{2},x_{3},x_{4},x_{5}$张卡片(若$x_{1}<0$,则表示B同学调给A同学$|x_{1}|$张卡片,$x_{2},x_{3},x_{4},x_{5}$亦如此).由题意,得$6+x_{1}-x_{2}=9+x_{2}-x_{3}=3+x_{3}-x_{4}=10+x_{4}-x_{5}=12+x_{5}-x_{1}=\frac{1}{5}×(12+6+9+3+10)=8$,所以$x_{2}=x_{1}-2$,$x_{3}=x_{1}-1$,$x_{4}=x_{1}-6$,$x_{5}=x_{1}-4$,所以调动卡片的总张数为$|x_{1}|+|x_{2}|+|x_{3}|+|x_{4}|+|x_{5}|=|x_{1}|+|x_{1}-2|+|x_{1}-1|+|x_{1}-6|+|x_{1}-4|$,等于数轴上表示数$x_{1}$的点与分别表示0,2,1,6,4的五点之间的距离之和,所以当$x_{1}=2$时,调动卡片的总张数最少,且最小值为$2+0+1+4+2=9$,此时$x_{1}=2$,$x_{2}=0$,$x_{3}=1$,$x_{4}=-4$,$x_{5}=-2$,所以应让A同学给B同学2张卡片,C同学给D同学1张卡片,E同学给D同学4张卡片,A同学给E同学2张卡片,这样调动的卡片总张数最少,最少调动9张.
答案:(1)3 4
(2)$|x+1|$ 1或-3
(3)$-1\leqslant x\leqslant2$ 解析:由题意,得$|x+1|+|x-2|$的值等于数轴上表示数x的点与分别表示-1,2的两点之间的距离之和,所以当$-1\leqslant x\leqslant2$时,$|x+1|+|x-2|$取最小值.
(4)2 解析:由题意,得$|x+1|+|x-2|+|x-4|$的值等于数轴上表示数x的点与分别表示-1,2,4的三点之间的距离之和,所以当$x=2$时,$|x+1|+|x-2|+|x-4|$取最小值.
(5)设A,B,C,D,E五名同学按顺时针方向依次调给相邻同学$x_{1},x_{2},x_{3},x_{4},x_{5}$张卡片(若$x_{1}<0$,则表示B同学调给A同学$|x_{1}|$张卡片,$x_{2},x_{3},x_{4},x_{5}$亦如此).由题意,得$6+x_{1}-x_{2}=9+x_{2}-x_{3}=3+x_{3}-x_{4}=10+x_{4}-x_{5}=12+x_{5}-x_{1}=\frac{1}{5}×(12+6+9+3+10)=8$,所以$x_{2}=x_{1}-2$,$x_{3}=x_{1}-1$,$x_{4}=x_{1}-6$,$x_{5}=x_{1}-4$,所以调动卡片的总张数为$|x_{1}|+|x_{2}|+|x_{3}|+|x_{4}|+|x_{5}|=|x_{1}|+|x_{1}-2|+|x_{1}-1|+|x_{1}-6|+|x_{1}-4|$,等于数轴上表示数$x_{1}$的点与分别表示0,2,1,6,4的五点之间的距离之和,所以当$x_{1}=2$时,调动卡片的总张数最少,且最小值为$2+0+1+4+2=9$,此时$x_{1}=2$,$x_{2}=0$,$x_{3}=1$,$x_{4}=-4$,$x_{5}=-2$,所以应让A同学给B同学2张卡片,C同学给D同学1张卡片,E同学给D同学4张卡片,A同学给E同学2张卡片,这样调动的卡片总张数最少,最少调动9张.
(2)$|x+1|$ 1或-3
(3)$-1\leqslant x\leqslant2$ 解析:由题意,得$|x+1|+|x-2|$的值等于数轴上表示数x的点与分别表示-1,2的两点之间的距离之和,所以当$-1\leqslant x\leqslant2$时,$|x+1|+|x-2|$取最小值.
(4)2 解析:由题意,得$|x+1|+|x-2|+|x-4|$的值等于数轴上表示数x的点与分别表示-1,2,4的三点之间的距离之和,所以当$x=2$时,$|x+1|+|x-2|+|x-4|$取最小值.
(5)设A,B,C,D,E五名同学按顺时针方向依次调给相邻同学$x_{1},x_{2},x_{3},x_{4},x_{5}$张卡片(若$x_{1}<0$,则表示B同学调给A同学$|x_{1}|$张卡片,$x_{2},x_{3},x_{4},x_{5}$亦如此).由题意,得$6+x_{1}-x_{2}=9+x_{2}-x_{3}=3+x_{3}-x_{4}=10+x_{4}-x_{5}=12+x_{5}-x_{1}=\frac{1}{5}×(12+6+9+3+10)=8$,所以$x_{2}=x_{1}-2$,$x_{3}=x_{1}-1$,$x_{4}=x_{1}-6$,$x_{5}=x_{1}-4$,所以调动卡片的总张数为$|x_{1}|+|x_{2}|+|x_{3}|+|x_{4}|+|x_{5}|=|x_{1}|+|x_{1}-2|+|x_{1}-1|+|x_{1}-6|+|x_{1}-4|$,等于数轴上表示数$x_{1}$的点与分别表示0,2,1,6,4的五点之间的距离之和,所以当$x_{1}=2$时,调动卡片的总张数最少,且最小值为$2+0+1+4+2=9$,此时$x_{1}=2$,$x_{2}=0$,$x_{3}=1$,$x_{4}=-4$,$x_{5}=-2$,所以应让A同学给B同学2张卡片,C同学给D同学1张卡片,E同学给D同学4张卡片,A同学给E同学2张卡片,这样调动的卡片总张数最少,最少调动9张.