8. 已知有理数x,y满足$|x - 1|+|y + 3| = 0$,则$x + y = $
-2
.答案:-2
解析:
因为$|x - 1| \geq 0$,$|y + 3| \geq 0$,且$|x - 1| + |y + 3| = 0$,所以$|x - 1| = 0$,$|y + 3| = 0$。
由$|x - 1| = 0$得$x - 1 = 0$,解得$x = 1$。
由$|y + 3| = 0$得$y + 3 = 0$,解得$y = -3$。
则$x + y = 1 + (-3) = -2$。
-2
由$|x - 1| = 0$得$x - 1 = 0$,解得$x = 1$。
由$|y + 3| = 0$得$y + 3 = 0$,解得$y = -3$。
则$x + y = 1 + (-3) = -2$。
-2
9. 若$a - b = -2$,则代数式$3(b - a)^{2}-b + a$的值为
10
.答案:10
解析:
因为$a - b=-2$,所以$b - a=2$。
$3(b - a)^{2}-b + a=3(b - a)^{2}+(a - b)$
将$b - a=2$,$a - b=-2$代入上式得:
$3×2^{2}+(-2)=3×4 - 2=12 - 2=10$
10
$3(b - a)^{2}-b + a=3(b - a)^{2}+(a - b)$
将$b - a=2$,$a - b=-2$代入上式得:
$3×2^{2}+(-2)=3×4 - 2=12 - 2=10$
10
10. 若关于x,y的多项式$mx^{3}+3nxy^{2}-2x^{3}-xy^{2}+2x + y$中不含三次项,则代数式$2m + 3n$的值是
5
.答案:5
解析:
$mx^{3}+3nxy^{2}-2x^{3}-xy^{2}+2x + y$
$=(m-2)x^{3}+(3n-1)xy^{2}+2x + y$
因为多项式不含三次项,所以三次项系数为0,即:
$\begin{cases}m - 2 = 0 \\ 3n - 1 = 0\end{cases}$
解得:$\begin{cases}m = 2 \\ n = \dfrac{1}{3}\end{cases}$
则$2m + 3n = 2×2 + 3×\dfrac{1}{3}=4 + 1 = 5$
5
$=(m-2)x^{3}+(3n-1)xy^{2}+2x + y$
因为多项式不含三次项,所以三次项系数为0,即:
$\begin{cases}m - 2 = 0 \\ 3n - 1 = 0\end{cases}$
解得:$\begin{cases}m = 2 \\ n = \dfrac{1}{3}\end{cases}$
则$2m + 3n = 2×2 + 3×\dfrac{1}{3}=4 + 1 = 5$
5
11. 如图是一个“数值转换机”的示意图. 若输入的$x = -5,y = 3$,则输出的结果为
26
.答案:26
解析:
$(-5)^2 + 3^3 = 25 + 27 = 52$,$52 ÷ 2 = 26$
26
26
12. 新趋势 传统文化 我国古书《易经》中有“上古结绳而治”的记载,它指“结绳记事”或“结绳记数”. 一远古牧人在从右到左依次排列的绳子上打结,满5进1,用来记录他所放牧的羊的只数. 如图①,他所放牧的羊的只数是$2×5^{2}+1×5 + 3 = 58$,则图②所代表的数是______
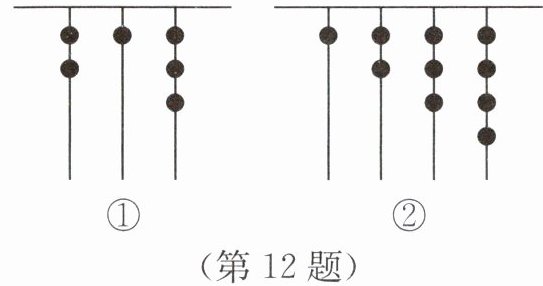
194
.
答案:194
解析:
$1×5^{3}+2×5^{2}+3×5 + 4 = 194$
13. 给出下列说法:①若$\frac{a}{b} = -1$,则a,b互为相反数;②若$a + b<0,\frac{b}{a}>0$,则$|a + 2b| = -a - 2b$;③若$-1<a<0$,则$a^{2}>-\frac{1}{a}$;④若$a + b + c<0,ab>0,c>0$,则$|-a| = -a$. 其中正确的是
①②④
.(填序号)答案:①②④ 解析:若a/b=-1,则a=-b,即a,b互为相反数,故①正确;若a+b<0,b/a>0,则a<0,b<0,所以a+2b<0,所以|a+2b|=-a-2b,故②正确;若-1<a<0,则0<a²<1,-1/a>1,所以a²<-1/a,故③错误;若a+b+c<0,ab>0,c>0,则a,b同号,a+b<0,所以a<0,b<0,所以|-a|=-a,故④正确.
14. (2025·江苏连云港期末)如图,一组按规律排列的图案由边长相同的正方形和等边三角形镶嵌而成,其中第1个图案中有4个等边三角形,第2个图案中有7个等边三角形,第3个图案中有10个等边三角形,…,则第n个图案中有
3n+1
个等边三角形.答案:(3n+1) 解析:因为第1个图案中有3×1+1=4(个)等边三角形,第2个图案中有3×2+1=7(个)等边三角形,第3个图案中有3×3+1=10(个)等边三角形,…,所以按此规律排列,第n个图案中有(3n+1)个等边三角形.
解析:
$3n + 1$
15. (16分)新素养 运算能力 计算:
(1)$(-20)+(+3)-(-5)-(+7)$;
(2)$[(-2)^{3}+\frac{4}{3}]÷4+(-\frac{2}{3})$;
(3)$(\frac{2}{3}-\frac{3}{4}+\frac{7}{8})÷\frac{1}{24}-(-1)^{2025}$;
(4)$-1^{6}-(0.5-\frac{2}{3})÷\frac{1}{3}×[-2-(-3)^{3}]-\frac{1}{8}$.
(1)$(-20)+(+3)-(-5)-(+7)$;
(2)$[(-2)^{3}+\frac{4}{3}]÷4+(-\frac{2}{3})$;
(3)$(\frac{2}{3}-\frac{3}{4}+\frac{7}{8})÷\frac{1}{24}-(-1)^{2025}$;
(4)$-1^{6}-(0.5-\frac{2}{3})÷\frac{1}{3}×[-2-(-3)^{3}]-\frac{1}{8}$.
答案:(1)-19. (2)-7/3. (3)20. (4)91/8.
解析:
(1)
$\begin{aligned}(-20)+(+3)-(-5)-(+7)&=-20 + 3 + 5 - 7\\&=(-20 - 7)+(3 + 5)\\&=-27 + 8\\&=-19\end{aligned}$
(2)
$\begin{aligned}[(-2)^{3}+\frac{4}{3}]÷4+(-\frac{2}{3})&=(-8 + \frac{4}{3})×\frac{1}{4}-\frac{2}{3}\\&=(-\frac{24}{3}+\frac{4}{3})×\frac{1}{4}-\frac{2}{3}\\&=(-\frac{20}{3})×\frac{1}{4}-\frac{2}{3}\\&=-\frac{5}{3}-\frac{2}{3}\\&=-\frac{7}{3}\end{aligned}$
(3)
$\begin{aligned}(\frac{2}{3}-\frac{3}{4}+\frac{7}{8})÷\frac{1}{24}-(-1)^{2025}&=(\frac{2}{3}-\frac{3}{4}+\frac{7}{8})×24 - (-1)\\&=\frac{2}{3}×24 - \frac{3}{4}×24 + \frac{7}{8}×24 + 1\\&=16 - 18 + 21 + 1\\&=(16 - 18)+(21 + 1)\\&=-2 + 22\\&=20\end{aligned}$
(4)
$\begin{aligned}-1^{6}-(0.5-\frac{2}{3})÷\frac{1}{3}×[-2-(-3)^{3}]-\frac{1}{8}&=-1 - (\frac{1}{2}-\frac{2}{3})×3×[-2 - (-27)]-\frac{1}{8}\\&=-1 - (-\frac{1}{6})×3×25 - \frac{1}{8}\\&=-1 + \frac{1}{2}×25 - \frac{1}{8}\\&=-1 + \frac{25}{2} - \frac{1}{8}\\&=-\frac{8}{8}+\frac{100}{8}-\frac{1}{8}\\&=\frac{91}{8}\end{aligned}$
$\begin{aligned}(-20)+(+3)-(-5)-(+7)&=-20 + 3 + 5 - 7\\&=(-20 - 7)+(3 + 5)\\&=-27 + 8\\&=-19\end{aligned}$
(2)
$\begin{aligned}[(-2)^{3}+\frac{4}{3}]÷4+(-\frac{2}{3})&=(-8 + \frac{4}{3})×\frac{1}{4}-\frac{2}{3}\\&=(-\frac{24}{3}+\frac{4}{3})×\frac{1}{4}-\frac{2}{3}\\&=(-\frac{20}{3})×\frac{1}{4}-\frac{2}{3}\\&=-\frac{5}{3}-\frac{2}{3}\\&=-\frac{7}{3}\end{aligned}$
(3)
$\begin{aligned}(\frac{2}{3}-\frac{3}{4}+\frac{7}{8})÷\frac{1}{24}-(-1)^{2025}&=(\frac{2}{3}-\frac{3}{4}+\frac{7}{8})×24 - (-1)\\&=\frac{2}{3}×24 - \frac{3}{4}×24 + \frac{7}{8}×24 + 1\\&=16 - 18 + 21 + 1\\&=(16 - 18)+(21 + 1)\\&=-2 + 22\\&=20\end{aligned}$
(4)
$\begin{aligned}-1^{6}-(0.5-\frac{2}{3})÷\frac{1}{3}×[-2-(-3)^{3}]-\frac{1}{8}&=-1 - (\frac{1}{2}-\frac{2}{3})×3×[-2 - (-27)]-\frac{1}{8}\\&=-1 - (-\frac{1}{6})×3×25 - \frac{1}{8}\\&=-1 + \frac{1}{2}×25 - \frac{1}{8}\\&=-1 + \frac{25}{2} - \frac{1}{8}\\&=-\frac{8}{8}+\frac{100}{8}-\frac{1}{8}\\&=\frac{91}{8}\end{aligned}$