1.(2024·广西)下列选项记录了我国四个直辖市某年一月份的平均气温,其中平均气温最低的是(
A.北京$-4.6^{\circ }C$
B.上海$5.8^{\circ }C$
C.天津$-3.2^{\circ }C$
D.重庆$8.1^{\circ }C$
A
)A.北京$-4.6^{\circ }C$
B.上海$5.8^{\circ }C$
C.天津$-3.2^{\circ }C$
D.重庆$8.1^{\circ }C$
答案:A
解析:
将四个直辖市的平均气温按从小到大排序:$-4.6^{\circ}C < -3.2^{\circ}C < 5.8^{\circ}C < 8.1^{\circ}C$,平均气温最低的是北京。
A
A
2.新趋势情境素材(2024·湖南长沙)“玉兔号”是我国首辆月球车,它和着陆器共同组成“嫦娥三号”探测器.“玉兔号”月球车能够耐受月球表面的最低温度是$-180^{\circ }C$,最高温度是$150^{\circ }C$,则它能够耐受的温差是(
A.$-180^{\circ }C$
B.$150^{\circ }C$
C.$30^{\circ }C$
D.$330^{\circ }C$
D
)A.$-180^{\circ }C$
B.$150^{\circ }C$
C.$30^{\circ }C$
D.$330^{\circ }C$
答案:D
解析:
温差 = 最高温度 - 最低温度 = $150 - (-180) = 150 + 180 = 330^{\circ}C$
D
D
3.(2024·内蒙古赤峰)如图,数轴上点A,M,B分别表示数$a,a+b,b$,则下列运算结果一定是正数的是(
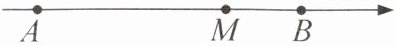
A.$a+b$
B.$a-b$
C.$ab$
D.$|a|-b$
A
)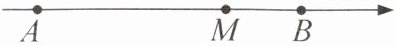
A.$a+b$
B.$a-b$
C.$ab$
D.$|a|-b$
答案:A
解析:
由数轴知:点A在点M左侧,点M在点B左侧,即$a < a+b < b$。
由$a+b < b$得$a < 0$;由$a < a+b$得$b > 0$。
A选项:$a+b$为点M表示的数,位于原点右侧(因$a+b < b$且$b > 0$),故$a+b > 0$。
B选项:$a - b$,$a < 0$,$b > 0$,则$a - b < 0$。
C选项:$ab$,$a < 0$,$b > 0$,则$ab < 0$。
D选项:$|a| - b$,$|a| = -a$,无法确定$-a$与$b$大小关系,结果可能为正、负或零。
A
由$a+b < b$得$a < 0$;由$a < a+b$得$b > 0$。
A选项:$a+b$为点M表示的数,位于原点右侧(因$a+b < b$且$b > 0$),故$a+b > 0$。
B选项:$a - b$,$a < 0$,$b > 0$,则$a - b < 0$。
C选项:$ab$,$a < 0$,$b > 0$,则$ab < 0$。
D选项:$|a| - b$,$|a| = -a$,无法确定$-a$与$b$大小关系,结果可能为正、负或零。
A
4.适合$|2a+7|+|2a-1|= 8$的整数a的值的个数是(
A.2
B.4
C.8
D.16
B
)A.2
B.4
C.8
D.16
答案:B
解析:
令$2a+7=0$,得$a=-\frac{7}{2}$;令$2a-1=0$,得$a=\frac{1}{2}$。
当$a<-\frac{7}{2}$时,$|2a+7|+|2a-1|=-(2a+7)-(2a-1)=-4a-6=8$,解得$a=-\frac{7}{2}$,不满足$a<-\frac{7}{2}$,舍去。
当$-\frac{7}{2}\leq a\leq\frac{1}{2}$时,$|2a+7|+|2a-1|=(2a+7)-(2a-1)=8$,等式恒成立。
当$a>\frac{1}{2}$时,$|2a+7|+|2a-1|=(2a+7)+(2a-1)=4a+6=8$,解得$a=\frac{1}{2}$,不满足$a>\frac{1}{2}$,舍去。
综上,$-\frac{7}{2}\leq a\leq\frac{1}{2}$,整数$a$为$-3,-2,-1,0$,共4个。
B
当$a<-\frac{7}{2}$时,$|2a+7|+|2a-1|=-(2a+7)-(2a-1)=-4a-6=8$,解得$a=-\frac{7}{2}$,不满足$a<-\frac{7}{2}$,舍去。
当$-\frac{7}{2}\leq a\leq\frac{1}{2}$时,$|2a+7|+|2a-1|=(2a+7)-(2a-1)=8$,等式恒成立。
当$a>\frac{1}{2}$时,$|2a+7|+|2a-1|=(2a+7)+(2a-1)=4a+6=8$,解得$a=\frac{1}{2}$,不满足$a>\frac{1}{2}$,舍去。
综上,$-\frac{7}{2}\leq a\leq\frac{1}{2}$,整数$a$为$-3,-2,-1,0$,共4个。
B
5.新趋势传统文化(2025·江苏宿迁期末)幻方历史悠久,传说最早出现在我国夏禹时代的“洛书”.如图是一个三阶幻方,它的规则如下:将幻方中的每一横行、每一竖列、每一条斜对角线(共2条)上的3个数分别相加,和都相等,则x的值为(

A.6
B.3
C.2
D.1
B
)
A.6
B.3
C.2
D.1
答案:B
6.如图所示的数阵叫“莱布尼茨调和三角形”,它们是由整数的倒数组成的,第n行有n个数,且两端的数均为$\frac {1}{n}$,每个数是它下一行左右相邻两数的和,则第8行第3个数(从左往右数)为(
A.$\frac {1}{60}$
B.$\frac {1}{168}$
C.$\frac {1}{252}$
D.$\frac {1}{280}$
B
)A.$\frac {1}{60}$
B.$\frac {1}{168}$
C.$\frac {1}{252}$
D.$\frac {1}{280}$
答案:B 解析:由题意,得第5行的数分别为$\frac{1}{5}$,$\frac{1}{20}$,$\frac{1}{30}$,$\frac{1}{20}$,$\frac{1}{5}$. 因为第3行第3个数为$\frac{1}{3}=\frac{1}{1×2}-\frac{1}{2×3}$,第4行第3个数为$\frac{1}{12}=\frac{1}{2×3}-\frac{1}{3×4}$,第5行第3个数为$\frac{1}{30}=\frac{1}{3×4}-\frac{1}{4×5}$,…,所以依此规律排列,第8行第3个数为$\frac{1}{6×7}-\frac{1}{7×8}=\frac{1}{168}$.
7.如图,用三个如图①所示的长方形和两个如图②所示的长方形以两种方式去覆盖一个大长方形ABCD,两种方式未覆盖的部分(阴影部分)的周长相等,那么图①中长方形的面积$S_{1}$与图②中长方形的面积$S_{2}$的比为(
A.$2:3$
B.$1:2$
C.$3:4$
D.$1:1$
A
)A.$2:3$
B.$1:2$
C.$3:4$
D.$1:1$
答案:A 解析:设题图①中长方形相邻两边的长分别为$a$,$b(a>b)$,题图②中长方形相邻两边的长分别为$x$,$y(x>y)$,边AB的长为$m$,边AD的长为$n$. 由题图,得$n=3b+2x=a+y$. 因为题图中阴影部分的周长相等,所以$2(3b+2x+m-y)=2(a+y+m-3b)$,即$3b+2x-y=a+y-3b$,所以$y=3b$. 把$y=3b$代入$3b+2x=a+y$,得$3b+2x=a+3b$,所以$2x=a$,所以$S_{1}=ab=2xb$,$S_{2}=xy=3xb$,所以$S_{1}:S_{2}=2xb:3xb=2:3$.