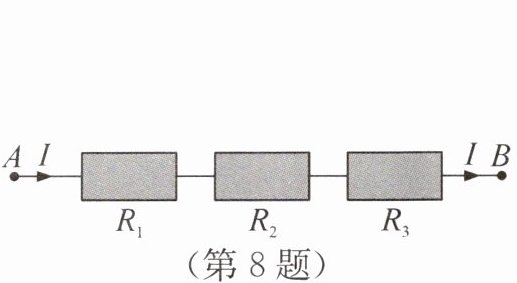
8.新趋势学科融合(2024·广东广州)如图,把$R_{1},R_{2},R_{3}$三个电阻串联起来,线路AB上的电流为I,电压为U,则$U= IR_{1}+IR_{2}+IR_{3}$.当$R_{1}= 20.3,R_{2}= 31.9,R_{3}= 47.8,I= 2.2$时,U的值为____
220
.
答案:220
解析:
$U = IR_{1} + IR_{2} + IR_{3} = I(R_{1} + R_{2} + R_{3})$,将$R_{1}=20.3$,$R_{2}=31.9$,$R_{3}=47.8$,$I=2.2$代入得:$R_{1} + R_{2} + R_{3}=20.3 + 31.9 + 47.8=100$,$U=2.2×100=220$。
220
220
9.亮点原创若$x= \frac {2024}{2025}$,则$|x-2|-|x-1|+|x|+|x+1|-|x+2|= $
$\frac{2024}{2025}$
.答案:$\frac{2024}{2025}$
解析:
因为$x = \frac{2024}{2025}$,所以$0 < x < 1$。
$|x - 2| = 2 - x$,$|x - 1| = 1 - x$,$|x| = x$,$|x + 1| = x + 1$,$|x + 2| = x + 2$。
原式$=(2 - x) - (1 - x) + x + (x + 1) - (x + 2)$
$=2 - x - 1 + x + x + x + 1 - x - 2$
$=(2 - 1 + 1 - 2) + (-x + x + x + x - x)$
$=0 + x$
$=x$
$=\frac{2024}{2025}$
$\frac{2024}{2025}$
$|x - 2| = 2 - x$,$|x - 1| = 1 - x$,$|x| = x$,$|x + 1| = x + 1$,$|x + 2| = x + 2$。
原式$=(2 - x) - (1 - x) + x + (x + 1) - (x + 2)$
$=2 - x - 1 + x + x + x + 1 - x - 2$
$=(2 - 1 + 1 - 2) + (-x + x + x + x - x)$
$=0 + x$
$=x$
$=\frac{2024}{2025}$
$\frac{2024}{2025}$
10.(2024·四川德阳)数学活动课上,甲组同学给乙组同学出示了一个探究问题:把数字1至8分别填入如图所示的八个圆圈内,使得任意两个有线段相连的圆圈内的数字之差的绝对值不等于1.经过探究后,乙组的小高同学填出了图中两个中心圆圈的数字a,b,则a可以是____

1或8
.
答案:1或8
11.为了保密,很多情况下都要采用密码进行交流,这时就要有破译密码的“钥匙”.英文字母表中的字母是按如下顺序排列的:abcdefghijklmnopqrstuvwxyz,现将26个字母首尾相接并按顺时针方向排成一个圈.规定若钥匙是“$x+2$”,则代表把一个字母换成字母圈中从它开始逆时针移动2位的字母,例如:密码“k”表示“i”,翻译成汉语就是“我”,又如密码“rgp”表示“pen”,翻译成汉语就是“钢笔”,此时代数式“$x+2$”就是破译此密码的“钥匙”.若密码“Fxjxpqrabkq”(英文字母大小写不影响)的钥匙是“$x-3$”,则此密码翻译成汉语是
我是一名学生
.答案:我是一名学生
解析:
将每个字母按钥匙“$x - 3$”(顺时针移动3位)转换:
F(6)→ 6 + 3 = 9 → I(我)
x(24)→ 24 + 3 = 27 → 27 - 26 = 1 → A(是)
j(10)→ 10 + 3 = 13 → M(一)
x(24)→ 24 + 3 = 27 → 27 - 26 = 1 → A(名)
p(16)→ 16 + 3 = 19 → S(学)
q(17)→ 17 + 3 = 20 → T(生)
r(18)→ 18 + 3 = 21 → U( )
a(1)→ 1 + 3 = 4 → D( )
b(2)→ 2 + 3 = 5 → E( )
k(11)→ 11 + 3 = 14 → N( )
q(17)→ 17 + 3 = 20 → T( )
我是一名学生
F(6)→ 6 + 3 = 9 → I(我)
x(24)→ 24 + 3 = 27 → 27 - 26 = 1 → A(是)
j(10)→ 10 + 3 = 13 → M(一)
x(24)→ 24 + 3 = 27 → 27 - 26 = 1 → A(名)
p(16)→ 16 + 3 = 19 → S(学)
q(17)→ 17 + 3 = 20 → T(生)
r(18)→ 18 + 3 = 21 → U( )
a(1)→ 1 + 3 = 4 → D( )
b(2)→ 2 + 3 = 5 → E( )
k(11)→ 11 + 3 = 14 → N( )
q(17)→ 17 + 3 = 20 → T( )
我是一名学生
12.新素养推理能力(2025·江苏南京期末)用同样大小的两种不同颜色的小正方形纸片,按如图所示的方式拼成正方形,则拼第90个正方形比拼第89个正方形多用
179
张小正方形纸片.答案:179
解析:
第1个正方形小正方形纸片总数:1
第2个正方形小正方形纸片总数:4
第n个正方形小正方形纸片总数:$n^2$
第90个正方形纸片数:$90^2 = 8100$
第89个正方形纸片数:$89^2 = 7921$
多用纸片数:$8100 - 7921 = 179$
179
第2个正方形小正方形纸片总数:4
第n个正方形小正方形纸片总数:$n^2$
第90个正方形纸片数:$90^2 = 8100$
第89个正方形纸片数:$89^2 = 7921$
多用纸片数:$8100 - 7921 = 179$
179
13.填在如图所示各方框中的三个数之间都具有相同的规律,则$x+y=$
593
.答案:593 解析:第一个方框中,$5=2^{2}+1$,$12=2×(5+1)$;第二个方框中,$17=4^{2}+1$,$72=4×(17+1)$;第三个方框中,$37=6^{2}+1$,$228=6×(37+1)$. 根据此规律,$x=8^{2}+1=65$,$y=8×(65+1)=528$,所以$x+y=593$.
14.(2024·重庆)一个各数位均不为0的四位自然数$M= \overline {abcd}$,若满足$a+d= b+c= 9$,则称这个四位数为“友谊数”.例如:四位数1278,因为$1+8= 2+7= 9$,所以1278是“友谊数”.若$\overline {abcd}$是一个“友谊数”,且$b-a= c-b= 1$,则这个数为
3456
;若$M= \overline {abcd}$是一个“友谊数”,设$F(M)= \frac {M}{9}$,且$\frac {F(M)+\overline {ab}+\overline {cd}}{13}$是整数,则满足条件的M的最大值是6273
.答案:3456 6273 解析:因为$M=\overline{abcd}$是一个“友谊数”,所以$M=1000a+100b+10c+d=1000a+100b+10(9-b)+(9-a)=999a+90b+99$,所以$F(M)=\frac{M}{9}=111a+10b+11$,所以$F(M)+\overline{ab}+\overline{cd}=111a+10b+11+10a+b+10(9-b)+(9-a)=120a+b+110$,所以$\frac{F(M)+\overline{ab}+\overline{cd}}{13}=\frac{120a+b+110}{13}=9a+8+\frac{3a+b+6}{13}$. 因为$\frac{F(M)+\overline{ab}+\overline{cd}}{13}$是整数,所以$\frac{3a+b+6}{13}$是整数,所以$3a+b+6$是13的倍数. 因为$a$,$b$,$c$,$d$是均不为0的正整数,且$a+d=b+c=9$,所以$1\leqslant a\leqslant8$,$1\leqslant b\leqslant8$. 当$a=8$时,$31\leqslant3a+b+6\leqslant38$,不合题意,舍去;当$a=7$时,$28\leqslant3a+b+6\leqslant35$,不合题意,舍去;当$a=6$时,$25\leqslant3a+b+6\leqslant32$,则$3a+b+6=26$,所以$b=2$,所以$c=7$,$d=3$,所以$M=6273$. 故$M$的最大值是6273.
解析:
3456 6273