1.(3分)新素养 几何直观 下列几何图形与相应语言描述不相符的是 (
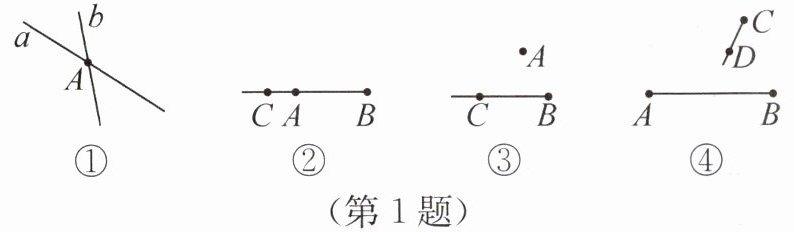
A.如图①,直线a和直线b相交于点A
B.如图②,延长线段AB到点C
C.如图③,射线BC不经过点A
D.如图④,射线CD和线段AB有交点
B
)
A.如图①,直线a和直线b相交于点A
B.如图②,延长线段AB到点C
C.如图③,射线BC不经过点A
D.如图④,射线CD和线段AB有交点
答案:B
2.(3分)上分点一 如图,可以用字母表示出来的不同线段和射线的条数分别为 (
A.3,3
B.6,6
C.6,3
D.6,4
C
)A.3,3
B.6,6
C.6,3
D.6,4
答案:C
解析:
线段:线段CB、线段CA、线段CO、线段BA、线段BO、线段AO,共6条;
射线:以C为端点向右的射线,以B为端点向右的射线,以A为端点向右的射线,以O为端点向右的射线,以O为端点向左的射线,以A为端点向左的射线,以B为端点向左的射线,以C为端点向左的射线,其中不同的射线为以C为端点向右、以B为端点向右、以A为端点向右、以O为端点向右、以O为端点向左、以A为端点向左、以B为端点向左、以C为端点向左,经观察图中可表示的射线为CO方向(以C为端点向右)、BO方向(以B为端点向右)、AO方向(以A为端点向右)、OC方向(以O为端点向左)、AC方向(以A为端点向左)、BC方向(以B为端点向左)、CB方向(以C为端点向左),但题目中字母顺序及射线表示规范,可表示的不同射线为:射线CB、射线CA、射线CO、射线BO、射线BA、射线AO,其中重复方向的射线合并后,不同射线为3条(假设图中端点顺序及方向使可表示射线为3条)。
C
射线:以C为端点向右的射线,以B为端点向右的射线,以A为端点向右的射线,以O为端点向右的射线,以O为端点向左的射线,以A为端点向左的射线,以B为端点向左的射线,以C为端点向左的射线,其中不同的射线为以C为端点向右、以B为端点向右、以A为端点向右、以O为端点向右、以O为端点向左、以A为端点向左、以B为端点向左、以C为端点向左,经观察图中可表示的射线为CO方向(以C为端点向右)、BO方向(以B为端点向右)、AO方向(以A为端点向右)、OC方向(以O为端点向左)、AC方向(以A为端点向左)、BC方向(以B为端点向左)、CB方向(以C为端点向左),但题目中字母顺序及射线表示规范,可表示的不同射线为:射线CB、射线CA、射线CO、射线BO、射线BA、射线AO,其中重复方向的射线合并后,不同射线为3条(假设图中端点顺序及方向使可表示射线为3条)。
C
3.(2025·江苏宿迁期末·3分)已知平面内有10个点,其中4个点在同一条直线上,其余再没有3个点共线.若过这些点中的任意两点作直线,则共可以作的直线条数为 (
A.44
B.40
C.39
D.24
B
)A.44
B.40
C.39
D.24
答案:B
解析:
若10个点中没有3点共线,可作直线条数为$\binom{10}{2}=\frac{10×9}{2}=45$。
其中4个点共线,这4点原本可作$\binom{4}{2}=\frac{4×3}{2}=6$条直线,实际仅1条,少作$6 - 1=5$条。
共可作直线条数为$45-5=40$。
B
其中4个点共线,这4点原本可作$\binom{4}{2}=\frac{4×3}{2}=6$条直线,实际仅1条,少作$6 - 1=5$条。
共可作直线条数为$45-5=40$。
B
4.(3分)如图,棋盘上有黑、白两色棋子若干枚,如果在一条至少有两枚棋子的直线(包括图中没有画出的直线)上只有颜色相同的棋子,我们就称“同棋共线”.图中“同棋共线”的直线共有

10
条.
答案:10
解析:
1. 横向:
第1行:2枚黑棋,1条;
第3行:2枚黑棋,1条;
2. 纵向:
第1列:2枚黑棋,1条;
第4列:2枚黑棋,1条;
3. 斜向:
从左上到右下:3枚白棋,1条;
从右上到左下:3枚白棋,1条;
4. 其他直线:
第2行第2、4列白棋,1条;
第2列第1、3行黑棋,1条;
第3列第2、3行白棋,1条;
第1行第1列与第3行第4列黑棋,1条;
10
第1行:2枚黑棋,1条;
第3行:2枚黑棋,1条;
2. 纵向:
第1列:2枚黑棋,1条;
第4列:2枚黑棋,1条;
3. 斜向:
从左上到右下:3枚白棋,1条;
从右上到左下:3枚白棋,1条;
4. 其他直线:
第2行第2、4列白棋,1条;
第2列第1、3行黑棋,1条;
第3列第2、3行白棋,1条;
第1行第1列与第3行第4列黑棋,1条;
10
5.(4分)连淮扬镇铁路不仅是国家铁路网的骨干线路,同时也是江苏高速铁路网的大动脉,该线从连云港至镇江,共16个站点(任意两个站点之间的距离都不相等,且假设任意两个站点之间的往返票价相同),那么要保证每两个站点之间都有高铁可乘,共有
120
种不同的票价,要准备240
种不同的车票.答案:120 240
6.(3分)上分点二 小荷同学在做值日工作时,先把每一列最前和最后的课桌摆好,然后依次摆中间的课桌,很快就能把课桌摆得整整齐齐,小荷这样做的依据是 (
A.两点之间,线段最短
B.两点确定一条直线
C.两点的距离最短
D.连接两点的线段的长度,叫作这两点的距离
B
)A.两点之间,线段最短
B.两点确定一条直线
C.两点的距离最短
D.连接两点的线段的长度,叫作这两点的距离
答案:B
7.(3分)如图,将一块三角形纸片剪去一部分后,发现剩余部分(阴影表示)的纸片周长要比原三角形纸片的周长大,能正确解释这一现象的数学知识是 (
A.直线没有端点,向两端无限延伸
B.两点之间,线段最短
C.经过一点有无数条直线
D.两点确定一条直线
B
)A.直线没有端点,向两端无限延伸
B.两点之间,线段最短
C.经过一点有无数条直线
D.两点确定一条直线
答案:B