8.(6分)新素养 几何直观 如图,草原上有四口油井,位于四边形ABCD的四个顶点上,现在要建立一个维修站H,试问H建在何处,才能使它到四口油井的距离之和HA+HB+HC+HD最小,请说明理由.
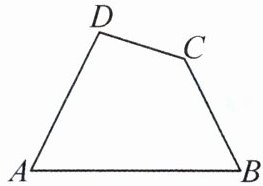

答案:H应建在AC,BD连线的交点处.理由如下:连接AC,BD,由两点之间线段最短可知,在AC,BD的交点H处建维修站才能使得HA+HB+HC+HD最小.
9.(3分)上分点三 把两条线段AB和CD放在同一条直线上比较长短时,下列说法错误的是 (
A.若线段AB的两个端点均落在线段CD的内部,则AB<CD
B.若点A,C重合,点B落在线段CD的内部,则AB<CD
C.若线段AB的一个端点在线段CD的内部,另一个端点在线段CD的外部,则AB>CD
D.若点B,D重合,点A,C位于点B的同侧,且点A在线段CD的外部,则AB>CD
C
)A.若线段AB的两个端点均落在线段CD的内部,则AB<CD
B.若点A,C重合,点B落在线段CD的内部,则AB<CD
C.若线段AB的一个端点在线段CD的内部,另一个端点在线段CD的外部,则AB>CD
D.若点B,D重合,点A,C位于点B的同侧,且点A在线段CD的外部,则AB>CD
答案:C
10.(3分)上分点四 两根木条,一根长10 cm,另一根长12 cm,将它们一端重合且放在同一条直线上,此时两根木条的中点之间的距离为 (
A.1 cm
B.11 cm
C.1 cm或11 cm
D.2 cm或11 cm
C
)A.1 cm
B.11 cm
C.1 cm或11 cm
D.2 cm或11 cm
答案:C
解析:
情况一:两根木条同向放置
两根木条中点到重合端的距离分别为:$\frac{10}{2}=5\,\text{cm}$,$\frac{12}{2}=6\,\text{cm}$
中点之间的距离为:$6 - 5=1\,\text{cm}$
情况二:两根木条反向放置
中点之间的距离为:$6 + 5=11\,\text{cm}$
综上,两根木条的中点之间的距离为$1\,\text{cm}$或$11\,\text{cm}$
C
两根木条中点到重合端的距离分别为:$\frac{10}{2}=5\,\text{cm}$,$\frac{12}{2}=6\,\text{cm}$
中点之间的距离为:$6 - 5=1\,\text{cm}$
情况二:两根木条反向放置
中点之间的距离为:$6 + 5=11\,\text{cm}$
综上,两根木条的中点之间的距离为$1\,\text{cm}$或$11\,\text{cm}$
C
11.(2025·江苏连云港期末·3分)如图,点A,B,C在同一条直线上,D为BC的中点,P为线段AC延长线上一动点(AD≠DP),E为AP的中点,则$\frac{AC - BP}{DE}$的值是
±2
.答案:±2 解析:设AB=x,BC=y,CP=z.分类讨论如下:①如图①,当AD>DP时,AD=AB+BD=x+$\frac{y}{2}$,AE=$\frac{1}{2}$(AB+BC+CP)=$\frac{x+y+z}{2}$,AC=AB+BC=x+y,BP=BC+CP=y+z,DE=AD−AE=$\frac{x - z}{2}$,AC−BP=x−z,则$\frac{AC−BP}{DE}$=2;②如图②,当AD<DP时,AD=AB+BD=x+$\frac{y}{2}$,AE=$\frac{1}{2}$(AB+BC+CP)=$\frac{x+y+z}{2}$,AC=AB+BC=x+y,BP=BC+CP=y+z,DE=AE−AD=$\frac{z - x}{2}$,AC−BP=x−z,则$\frac{AC−BP}{DE}$=−2.综上所述,$\frac{AC−BP}{DE}$的值是±2.
解析:
设$AB = x$,$BC = y$,$CP = z$。
①当$AD > DP$时:
$AD = AB + BD = x+\frac{y}{2}$,
$AE=\frac{1}{2}(AB + BC + CP)=\frac{x + y + z}{2}$,
$AC=AB + BC=x + y$,
$BP=BC + CP=y + z$,
$DE=AD - AE=\frac{x - z}{2}$,
$AC - BP=x - z$,
$\frac{AC - BP}{DE}=\frac{x - z}{\frac{x - z}{2}}=2$。
②当$AD < DP$时:
$AD = AB + BD=x+\frac{y}{2}$,
$AE=\frac{1}{2}(AB + BC + CP)=\frac{x + y + z}{2}$,
$AC=AB + BC=x + y$,
$BP=BC + CP=y + z$,
$DE=AE - AD=\frac{z - x}{2}$,
$AC - BP=x - z$,
$\frac{AC - BP}{DE}=\frac{x - z}{\frac{z - x}{2}}=-2$。
综上所述,$\frac{AC - BP}{DE}$的值是$\pm 2$。
$\pm 2$
①当$AD > DP$时:
$AD = AB + BD = x+\frac{y}{2}$,
$AE=\frac{1}{2}(AB + BC + CP)=\frac{x + y + z}{2}$,
$AC=AB + BC=x + y$,
$BP=BC + CP=y + z$,
$DE=AD - AE=\frac{x - z}{2}$,
$AC - BP=x - z$,
$\frac{AC - BP}{DE}=\frac{x - z}{\frac{x - z}{2}}=2$。
②当$AD < DP$时:
$AD = AB + BD=x+\frac{y}{2}$,
$AE=\frac{1}{2}(AB + BC + CP)=\frac{x + y + z}{2}$,
$AC=AB + BC=x + y$,
$BP=BC + CP=y + z$,
$DE=AE - AD=\frac{z - x}{2}$,
$AC - BP=x - z$,
$\frac{AC - BP}{DE}=\frac{x - z}{\frac{z - x}{2}}=-2$。
综上所述,$\frac{AC - BP}{DE}$的值是$\pm 2$。
$\pm 2$
12.(3分)如图,C是线段AB上的一点,D是线段CB的中点.已知图中所有线段的长度之和为23,线段AC的长度与线段CB的长度都是正整数,则线段AC的长度为______.


3
答案:3 解析:题图中共有六条线段,即AC,AD,AB,CD,CB,DB.又D是线段CB的中点,所以CD=DB,CB=2CD,AB=AC+2CD,AD=AC+CD.因为AC+AD+AB+CD+CB+DB=23,所以AC+AC+CD+AC+2CD+CD+2CD+CD=23,所以3AC+7CD=23,所以AC=$\frac{23−7CD}{3}$.因为线段AC 的长度与线段CB的长度都是正整数,所以CD=2,所以AC=3.
解析:
图中共有六条线段:AC,AD,AB,CD,CB,DB。
∵D是线段CB的中点,∴CD=DB,CB=2CD。
∵AB=AC+CB=AC+2CD,AD=AC+CD,
∴所有线段长度之和为:
AC+AD+AB+CD+CB+DB
=AC+(AC+CD)+(AC+2CD)+CD+2CD+CD
=3AC+7CD。
由题意得3AC+7CD=23,∴AC=$\frac{23-7CD}{3}$。
∵AC,CB为正整数,CB=2CD,∴CD为正整数。
当CD=2时,AC=$\frac{23-14}{3}=3$,符合题意。
故线段AC的长度为3。
3
∵D是线段CB的中点,∴CD=DB,CB=2CD。
∵AB=AC+CB=AC+2CD,AD=AC+CD,
∴所有线段长度之和为:
AC+AD+AB+CD+CB+DB
=AC+(AC+CD)+(AC+2CD)+CD+2CD+CD
=3AC+7CD。
由题意得3AC+7CD=23,∴AC=$\frac{23-7CD}{3}$。
∵AC,CB为正整数,CB=2CD,∴CD为正整数。
当CD=2时,AC=$\frac{23-14}{3}=3$,符合题意。
故线段AC的长度为3。
3
13.(10分)已知关于x的方程2(x - 3) - m = 2的解与方程3x - 7 = 2x的解相同.
(1)求m的值;
(2)已知线段AB = m,在直线AB上取一点P,恰好使AP = 2BP.若Q为BP的中点,求线段AQ的长.
(1)求m的值;
(2)已知线段AB = m,在直线AB上取一点P,恰好使AP = 2BP.若Q为BP的中点,求线段AQ的长.
答案:(1)解方程2(x−3)−m=2,得x=4+$\frac{m}{2}$.解方程3x−7=2x,得x=7.由题意,得4+$\frac{m}{2}$=7,解得m=6.
(2)由(1),得AB=6.因为AP=2BP,所以分类讨论如下:①当点P在线段AB上时,AB=AP+BP=3BP,所以BP=$\frac{1}{3}$AB=2,所以AP=4.因为Q为BP的中点,所以PQ=$\frac{1}{2}$BP=1,所以AQ=AP+PQ=5;②当点P在线段AB的延长线上时,AB=AP−BP=BP,所以BP=6.因为Q为BP的中点,所以BQ=$\frac{1}{2}$BP=3,所以AQ=AB+BQ=9.综上所述,线段AQ的长为5或9.
(2)由(1),得AB=6.因为AP=2BP,所以分类讨论如下:①当点P在线段AB上时,AB=AP+BP=3BP,所以BP=$\frac{1}{3}$AB=2,所以AP=4.因为Q为BP的中点,所以PQ=$\frac{1}{2}$BP=1,所以AQ=AP+PQ=5;②当点P在线段AB的延长线上时,AB=AP−BP=BP,所以BP=6.因为Q为BP的中点,所以BQ=$\frac{1}{2}$BP=3,所以AQ=AB+BQ=9.综上所述,线段AQ的长为5或9.