6.(3分)上分点二 将一副三角板按如图所示的方式放置,$30^{\circ }角和45^{\circ }$角共顶点.若$CM平分\angle ACD,CN平分\angle ACE$,则$\angle MCN$的度数是 (
A.$15^{\circ }$
B.$22.5^{\circ }$
C.$30^{\circ }$
D.无法确定
B
)A.$15^{\circ }$
B.$22.5^{\circ }$
C.$30^{\circ }$
D.无法确定
答案:B
7.(3分)如图,点$O在直线AB$上,$OD是\angle BOC$的平分线.若$\angle AOC= 140^{\circ }$,则$\angle BOD$的度数为
20°
.答案:20°
解析:
∵点$O$在直线$AB$上,$\angle AOC = 140^{\circ}$,
$\therefore \angle BOC=180^{\circ}-\angle AOC=180^{\circ}-140^{\circ}=40^{\circ}$。
∵$OD$是$\angle BOC$的平分线,
$\therefore \angle BOD=\frac{1}{2}\angle BOC=\frac{1}{2}×40^{\circ}=20^{\circ}$。
$20^{\circ}$
$\therefore \angle BOC=180^{\circ}-\angle AOC=180^{\circ}-140^{\circ}=40^{\circ}$。
∵$OD$是$\angle BOC$的平分线,
$\therefore \angle BOD=\frac{1}{2}\angle BOC=\frac{1}{2}×40^{\circ}=20^{\circ}$。
$20^{\circ}$
8.(3分)上分点三 如图,直线$AB,CD相交于点O$.若$\angle 1= 80^{\circ },\angle 2= 30^{\circ }$,则$\angle AOE$的度数为 (
A.$30^{\circ }$
B.$50^{\circ }$
C.$60^{\circ }$
D.$80^{\circ }$
B
)A.$30^{\circ }$
B.$50^{\circ }$
C.$60^{\circ }$
D.$80^{\circ }$
答案:B
解析:
∵直线$AB$,$CD$相交于点$O$,$\angle 1 = 80^{\circ}$
$\therefore \angle AOD=\angle 1 = 80^{\circ}$(对顶角相等)
$\because \angle 2 = 30^{\circ}$,$\angle AOD=\angle AOE+\angle 2$
$\therefore \angle AOE=\angle AOD-\angle 2=80^{\circ}-30^{\circ}=50^{\circ}$
B
$\therefore \angle AOD=\angle 1 = 80^{\circ}$(对顶角相等)
$\because \angle 2 = 30^{\circ}$,$\angle AOD=\angle AOE+\angle 2$
$\therefore \angle AOE=\angle AOD-\angle 2=80^{\circ}-30^{\circ}=50^{\circ}$
B
9.(3分)亮点原创 在同一平面内有$4$条直线,它们两两相交,且任意三条直线不交于同一点,则这$4$条直线一共形成
12
对对顶角.答案:12
解析:
每两条直线相交形成2对对顶角,4条直线两两相交,共有$\frac{4×3}{2}=6$个交点,每个交点形成2对对顶角,所以一共形成$6×2 = 12$对对顶角。
12
12
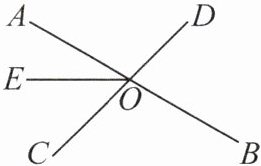
10.(2025·江苏南京期末·6分)如图,直线$AB,CD相交于点O$.已知$\angle BOD= 75^{\circ },OE把\angle AOC$分成两个角,且$\angle AOE= \frac {2}{3}\angle EOC$,将射线$OE绕点O逆时针旋转\alpha (0^{\circ }<\alpha <360^{\circ })到OF$,当$\angle AOF= 120^{\circ }$时,求$\alpha$的度数.

答案:
因为∠BOD=75°,所以∠AOC=∠BOD=75°.因为∠AOE=$\frac{2}{3}$∠EOC,所以∠AOE=$\frac{2}{5}$∠AOC=30°.分类讨论如下:① 当OF运动到如图①所示的位置时,因为∠AOF=120°,所以α=∠AOF - ∠AOE=90°;② 当OF运动到如图②所示的位置时,因为∠AOF=120°,所以α=360° - (∠AOF+∠AOE)=210°.综上所述,α的度数为90°或210°.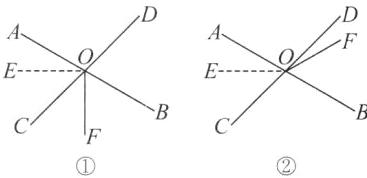
因为∠BOD=75°,所以∠AOC=∠BOD=75°.因为∠AOE=$\frac{2}{3}$∠EOC,所以∠AOE=$\frac{2}{5}$∠AOC=30°.分类讨论如下:① 当OF运动到如图①所示的位置时,因为∠AOF=120°,所以α=∠AOF - ∠AOE=90°;② 当OF运动到如图②所示的位置时,因为∠AOF=120°,所以α=360° - (∠AOF+∠AOE)=210°.综上所述,α的度数为90°或210°.

11.(3分)给出下列说法:①一条直线的垂线只有一条;②两条直线相交,交点叫作垂足;③互相垂直的两条直线所形成的四个角一定都是直角.其中正确的个数是 (
A.$0$
B.$1$
C.$2$
D.$3$
B
)A.$0$
B.$1$
C.$2$
D.$3$
答案:B
解析:
①一条直线的垂线有无数条,原说法错误;
②两条直线相交且成直角时,交点叫作垂足,原说法错误;
③互相垂直的两条直线所形成的四个角一定都是直角,原说法正确。
正确的个数是1。
B
②两条直线相交且成直角时,交点叫作垂足,原说法错误;
③互相垂直的两条直线所形成的四个角一定都是直角,原说法正确。
正确的个数是1。
B
12.(3分)亮点原创 已知平面内有不重合的两点$P,Q和直线l$,分别过点$P,Q作直线l$的垂线,可作的垂线有 (
A.$0条或1$条
B.$0条或2$条
C.$1条或2$条
D.无数条
C
)A.$0条或1$条
B.$0条或2$条
C.$1条或2$条
D.无数条
答案:C
解析:
当点$P$,$Q$在直线$l$上且重合时,过两点只能作$1$条垂线;当点$P$,$Q$在直线$l$上不重合或至少有一点不在直线$l$上时,可作$2$条垂线。故可作的垂线有$1$条或$2$条。
C
C
13.(3分)上分点四 噪声污染对人、动物、仪器仪表以及建筑物等均会构成危害,其危害程度主要取决于噪声的频率、强度及暴露时间.人距离声源越近,听到的声音越大,受到的危害就越大.如图,工厂$C$处有大型生产机器会产生较大噪声,人站在

D
(填“$A$”“$B$”或“$D$”)处受到的危害最大.
答案:D