6.(6分)如图,直线EF分别与直线AB,CD相交于点P和点Q,PG平分$∠BPQ$交CD于点G,QH平分$∠CQP$交AB于H,且$∠1= ∠2$.写出图中哪些直线互相平行,并说明理由.
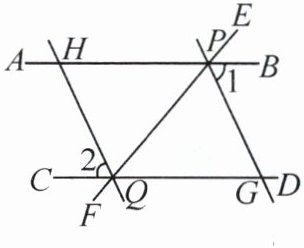

答案:QH//PG,AB//CD. 理由如下:因为 PG 平分∠BPQ,QH 平分∠CQP,所以∠GPQ=∠1=1/2∠BPQ,∠HQP=∠2=1/2∠CQP. 因为∠1=∠2,所以∠GPQ=∠HQP,∠BPQ=∠CQP,所以 QH//PG,AB//CD.
7.(2025·江苏常州期末·3分)新素养 推理能力 如图,已知射线OP//AE,$∠A= α$,依次作出$∠AOP$的平分线OB,$∠BOP的平分线OB_{1},∠B_{1}OP的平分线OB_{2},...,∠B_{2024}OP的平分线OB_{2025}$,其中点$B,B_{1},B_{2},...,B_{2025}$都在射线AE上,则$∠AB_{2025}O$的度数为 (
A.$\frac {180^{\circ }-α}{2^{2024}}$
B.$\frac {180^{\circ }-α}{2^{2025}}$
C.$\frac {180^{\circ }-α}{2^{2026}}$
D.$\frac {180^{\circ }-α}{2}$
C
)A.$\frac {180^{\circ }-α}{2^{2024}}$
B.$\frac {180^{\circ }-α}{2^{2025}}$
C.$\frac {180^{\circ }-α}{2^{2026}}$
D.$\frac {180^{\circ }-α}{2}$
答案:C 解析:因为 OP//AE,所以∠A+∠AOP=180°,∠ABO=∠BOP. 因为∠A=α,所以∠AOP=180°-α. 因为 OB 平分∠AOP,所以∠AOB=∠BOP=1/2∠AOP=1/2(180°-α),所以∠ABO=∠BOP=1/2(180°-α). 同理,得∠AB₁O=∠B₁OP=1/2∠BOP=1/2²(180°-α),∠AB₂O=1/2³(180°-α),…,则∠AB₂₀₂₅O=(180°-α)/2²⁰²⁶.
8.(3分)如图,已知直线$l_{1}// l_{2},∠α= ∠β$.若$∠1= 40^{\circ }$,则$∠2= $
140°
.答案:140°
解析:
延长∠α的一边交$l_{2}$于一点,设∠α的对顶角为∠3,∠β的对顶角为∠4。
∵$l_{1}//l_{2}$,
∴∠1=∠3(两直线平行,同位角相等)。
∵∠α=∠β,∠3=∠α,∠4=∠β(对顶角相等),
∴∠3=∠4。
∴∠3的一边与∠4的一边平行(内错角相等,两直线平行)。
∴∠2+∠1=180°(两直线平行,同旁内角互补)。
∵∠1=40°,
∴∠2=180° - 40°=140°。
140°
∵$l_{1}//l_{2}$,
∴∠1=∠3(两直线平行,同位角相等)。
∵∠α=∠β,∠3=∠α,∠4=∠β(对顶角相等),
∴∠3=∠4。
∴∠3的一边与∠4的一边平行(内错角相等,两直线平行)。
∴∠2+∠1=180°(两直线平行,同旁内角互补)。
∵∠1=40°,
∴∠2=180° - 40°=140°。
140°
9.(3分)上分点三 若两个角的两边分别平行,且一个角比另一个角的3倍少$60^{\circ }$,则这两个角的度数分别为
30°,30°或 120°,60°
.答案:30°,30°或 120°,60°
解析:
设其中一个角为$x^{\circ}$,则另一个角为$(3x - 60)^{\circ}$。
因为两个角的两边分别平行,所以这两个角相等或互补。
情况一:两角相等
$x = 3x - 60$
$2x = 60$
$x = 30$
则另一个角为$3×30 - 60 = 30^{\circ}$
情况二:两角互补
$x + (3x - 60) = 180$
$4x - 60 = 180$
$4x = 240$
$x = 60$
则另一个角为$3×60 - 60 = 120^{\circ}$
这两个角的度数分别为$30^{\circ}$,$30^{\circ}$或$120^{\circ}$,$60^{\circ}$
因为两个角的两边分别平行,所以这两个角相等或互补。
情况一:两角相等
$x = 3x - 60$
$2x = 60$
$x = 30$
则另一个角为$3×30 - 60 = 30^{\circ}$
情况二:两角互补
$x + (3x - 60) = 180$
$4x - 60 = 180$
$4x = 240$
$x = 60$
则另一个角为$3×60 - 60 = 120^{\circ}$
这两个角的度数分别为$30^{\circ}$,$30^{\circ}$或$120^{\circ}$,$60^{\circ}$
10.(3分)上分点四 给出下列说法:① 各边相等的三角形是正三角形;② 各角相等的多边形是正多边形;③ 各边相等的多边形是正多边形;④ 正多边形的边都相等;⑤ 正多边形的内角都相等;⑥ 正多边形的对角线都相等;⑦ 正多边形的外角都相等.其中错误的个数是 (
A.2
B.3
C.4
D.5
B
)A.2
B.3
C.4
D.5
答案:B
解析:
①正确;②错误(矩形各角相等但不是正多边形);③错误(菱形各边相等但不是正多边形);④正确;⑤正确;⑥错误(正五边形对角线不都相等);⑦正确。错误的是②③⑥,共3个。
B
B
11.(3分)如图所示为长方形ABCD,一条直线将该长方形分割成两个多边形.若这两个多边形的边数分别为a和b,则$a+b$的值不可能是 (
A.6
B.7
C.8
D.9
D
)A.6
B.7
C.8
D.9
答案:D
12.(4分)若过m边形的一个顶点有7条对角线,n边形没有对角线,k边形一共有k条对角线,则代数式$m\cdot (-k)^{n}$的值为 (
A.1 250
B.-1 250
C.1 000
D.-1 000
B
)A.1 250
B.-1 250
C.1 000
D.-1 000
答案:B
解析:
过$m$边形的一个顶点的对角线条数为$m - 3$,由题意得$m - 3 = 7$,解得$m = 10$。
$n$边形没有对角线,三角形没有对角线,故$n = 3$。
$k$边形的对角线条数公式为$\frac{k(k - 3)}{2}$,由题意得$\frac{k(k - 3)}{2}=k$,解得$k = 5$($k = 0$舍去)。
则$m\cdot (-k)^{n}=10× (-5)^{3}=10× (-125)=-1250$。
B
$n$边形没有对角线,三角形没有对角线,故$n = 3$。
$k$边形的对角线条数公式为$\frac{k(k - 3)}{2}$,由题意得$\frac{k(k - 3)}{2}=k$,解得$k = 5$($k = 0$舍去)。
则$m\cdot (-k)^{n}=10× (-5)^{3}=10× (-125)=-1250$。
B