1. (2024·吉林长春·3分)单项式$-2a^{2}b$的次数是
3
.答案:3
2. (3分)新趋势学科融合在朱自清的《春》中描写春雨“像牛毛,像花针,像细丝,密密地斜织着”的语句,这里把雨看成了线,这种生活现象可以反映的数学原理是
点动成线
.答案:点动成线
3. (2024·四川巴中·3分)从五边形的一个顶点出发可以引
2
条对角线.答案:2
4. (2024·广东广州·3分)如图,直线$l分别与直线a$,$b$相交,$a// b$.若$∠1= 71^{\circ }$,则$∠2$的度数为
$109^\circ$
.答案:$109^\circ$
解析:
因为$a // b$,所以$\angle 1$与$\angle 2$的邻补角相等。$\angle 1$的邻补角为$180^{\circ} - 71^{\circ} = 109^{\circ}$,所以$\angle 2 = 109^{\circ}$。
$109^{\circ}$
$109^{\circ}$
5. (2024·江苏南京·3分)如图,点$A$,$O$,$B$在同一条直线上,$OD是∠AOC$的平分线,$OE是∠BOC$的平分线.若$∠AOE= 162^{\circ }$,则$∠BOD= $
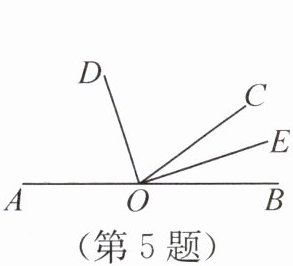
$108^\circ$
.
答案:$108^\circ$
解析:
∵点$A$,$O$,$B$在同一条直线上,
$\therefore \angle AOB=180^{\circ}$.
$\because \angle AOE = 162^{\circ}$,
$\therefore \angle BOE=\angle AOB-\angle AOE=180^{\circ}-162^{\circ}=18^{\circ}$.
$\because OE$是$\angle BOC$的平分线,
$\therefore \angle BOC = 2\angle BOE=2×18^{\circ}=36^{\circ}$.
$\therefore \angle AOC=\angle AOB-\angle BOC=180^{\circ}-36^{\circ}=144^{\circ}$.
$\because OD$是$\angle AOC$的平分线,
$\therefore \angle AOD=\frac{1}{2}\angle AOC=\frac{1}{2}×144^{\circ}=72^{\circ}$.
$\therefore \angle BOD=\angle AOB-\angle AOD=180^{\circ}-72^{\circ}=108^{\circ}$.
$108^{\circ}$
$\therefore \angle AOB=180^{\circ}$.
$\because \angle AOE = 162^{\circ}$,
$\therefore \angle BOE=\angle AOB-\angle AOE=180^{\circ}-162^{\circ}=18^{\circ}$.
$\because OE$是$\angle BOC$的平分线,
$\therefore \angle BOC = 2\angle BOE=2×18^{\circ}=36^{\circ}$.
$\therefore \angle AOC=\angle AOB-\angle BOC=180^{\circ}-36^{\circ}=144^{\circ}$.
$\because OD$是$\angle AOC$的平分线,
$\therefore \angle AOD=\frac{1}{2}\angle AOC=\frac{1}{2}×144^{\circ}=72^{\circ}$.
$\therefore \angle BOD=\angle AOB-\angle AOD=180^{\circ}-72^{\circ}=108^{\circ}$.
$108^{\circ}$
6. (2024·陕西·3分)小华探究“幻方”时,提出了一个问题:如图,将$0$,$-2$,$-1$,$1$,$2$这五个数分别填在五个小正方形内,使横向三个数之和与纵向三个数之和相等,则填入中间位置的小正方形内的数可以是
0
.(写出一个符合题意的数即可)答案:0(答案不唯一)
7. (2024·甘肃·3分)定义一种新运算“$*$”,规定运算法则如下:$m*n= m^{n}-mn$($m$,$n$均为整数,且$m≠0$).例如:$2*3= 2^{3}-2×3= 2$,则$(-2)*2= $
8
.答案:8
解析:
$(-2)*2=(-2)^{2}-(-2)×2=4+4=8$
8. (2024·湖南长沙·3分)为庆祝中国改革开放$46$周年,某中学举办了一场精彩纷呈的庆祝活动,现场参与者均为在校中学生,其中有一个活动项目是“选数字猜出生年份”,该活动项目主持人要求参与者从$1$,$2$,$3$,$4$,$5$,$6$,$7$,$8$,$9$这九个数字中任取一个数字,先乘以$10$,再加上$4.6$,将此时的运算结果再乘以$10$,然后加上$1978$,最后减去参与者的出生年份(注:出生年份是一个四位数,比如$2010年对应的四位数是2010$),得到最终的运算结果.只要参与者报出最终的运算结果,主持人立马就知道参与者的出生年份.若某位参与者报出的最终的运算结果是$915$,则这位参与者的出生年份是____
2009
.答案:2009
解析:
设参与者取的数字为$x$,出生年份为$y$。
根据题意可列方程:$[(10x + 4.6)×10 + 1978] - y = 915$
化简方程:$(100x + 46 + 1978) - y = 915$,即$100x + 2024 - y = 915$
则$y = 100x + 2024 - 915 = 100x + 1109$
因为$x$是$1 - 9$中的一个数字,且$y$是四位数出生年份,合理取值$x = 9$时,$y = 100×9 + 1109 = 2009$
2009
根据题意可列方程:$[(10x + 4.6)×10 + 1978] - y = 915$
化简方程:$(100x + 46 + 1978) - y = 915$,即$100x + 2024 - y = 915$
则$y = 100x + 2024 - 915 = 100x + 1109$
因为$x$是$1 - 9$中的一个数字,且$y$是四位数出生年份,合理取值$x = 9$时,$y = 100×9 + 1109 = 2009$
2009
9. (3分)新素养空间观念如图,在长$8\mathrm{c}\mathrm{m}、$宽$6\mathrm{c}\mathrm{m}$的大长方形中剪出一个长$4\mathrm{c}\mathrm{m}、$宽$3\mathrm{c}\mathrm{m}$的小长方形.现以该图形的对称轴为轴旋转一周,所得几何体的表面积为____

$92\pi$
$\mathrm{c}{\mathrm{m}}^{\mathrm{2}}.$
答案:$92\pi$
解析:
由图可知对称轴为大长方形的竖直对称轴。旋转后所得几何体为大圆柱挖去一个小圆柱。
大圆柱:底面半径$r_1 = 4\,\text{cm}$,高$h_1 = 6\,\text{cm}$,表面积$S_1 = 2\pi r_1^2 + 2\pi r_1 h_1 = 2\pi×4^2 + 2\pi×4×6 = 32\pi + 48\pi = 80\pi\,\text{cm}^2$。
小圆柱:底面半径$r_2 = 2\,\text{cm}$,高$h_2 = 3\,\text{cm}$,侧面积$S_{\text{侧}} = 2\pi r_2 h_2 = 2\pi×2×3 = 12\pi\,\text{cm}^2$,上下底面积$2\pi r_2^2 = 2\pi×2^2 = 8\pi\,\text{cm}^2$。
组合体表面积:$S = S_1 - 2\pi r_2^2 + S_{\text{侧}} = 80\pi - 8\pi + 12\pi = 84\pi\,\text{cm}^2$。
1
大圆柱:底面半径$r_1 = 4\,\text{cm}$,高$h_1 = 6\,\text{cm}$,表面积$S_1 = 2\pi r_1^2 + 2\pi r_1 h_1 = 2\pi×4^2 + 2\pi×4×6 = 32\pi + 48\pi = 80\pi\,\text{cm}^2$。
小圆柱:底面半径$r_2 = 2\,\text{cm}$,高$h_2 = 3\,\text{cm}$,侧面积$S_{\text{侧}} = 2\pi r_2 h_2 = 2\pi×2×3 = 12\pi\,\text{cm}^2$,上下底面积$2\pi r_2^2 = 2\pi×2^2 = 8\pi\,\text{cm}^2$。
组合体表面积:$S = S_1 - 2\pi r_2^2 + S_{\text{侧}} = 80\pi - 8\pi + 12\pi = 84\pi\,\text{cm}^2$。
1