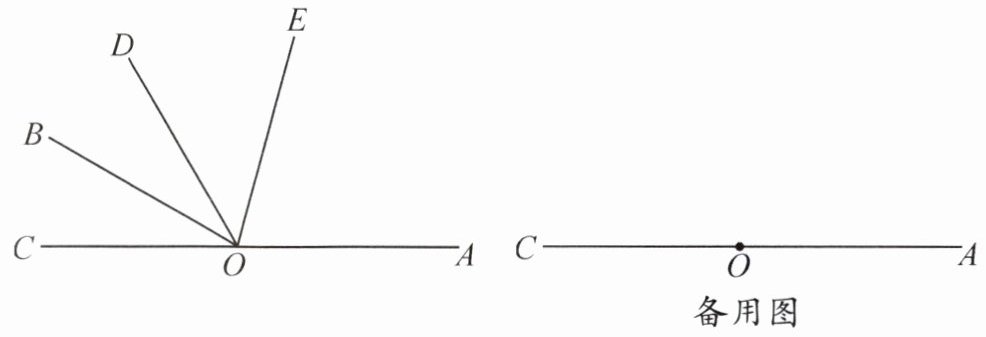
3.(2025·江苏盐城期末·13分)新素养 几何直观 如图,$O是直线AC$上一点,射线$OB$,$OD都不与射线OC$重合,$\angle AOB与\angle BOD$互为补角,$OE平分\angle AOB$.
(1)若$\angle AOB = 150^{\circ}$,则$\angle AOD = $____,$\angle DOE = $____;
(2)若$\angle DOE = 30^{\circ}$,求$\angle AOB$的度数;
(3)在$\angle BOE$,$\angle BOD$,$\angle DOE$这三个角中,当一个角的度数是另外一个角度数的$2$倍时,求$\angle AOB$的度数.
(1)若$\angle AOB = 150^{\circ}$,则$\angle AOD = $____,$\angle DOE = $____;
(2)若$\angle DOE = 30^{\circ}$,求$\angle AOB$的度数;
(3)在$\angle BOE$,$\angle BOD$,$\angle DOE$这三个角中,当一个角的度数是另外一个角度数的$2$倍时,求$\angle AOB$的度数.

答案:
(1)120° 45°
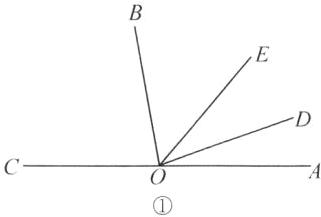
(2)设∠AOB = 2x°。因为∠AOB与∠BOD互为补角,所以∠BOD = 180° - ∠AOB=(180 - 2x)°。因为OE平分∠AOB,所以∠BOE = $\frac{1}{2}$∠AOB = x°。因为∠DOE = 30°,所以分类讨论如下:①如图①,当OE在∠BOD内部时,∠DOE = ∠BOD - ∠BOE=(180 - 3x)°,所以180 - 3x = 30,解得x = 50,所以∠AOB = 100°;②如图②,当OE在∠BOD外部时,∠DOE = ∠BOE - ∠BOD=(3x - 180)°,所以3x - 180 = 30,解得x = 70,所以∠AOB = 140°。

综上所述,∠AOB的度数为100°或140°。
(3)设∠AOB = 2y°,则同(2),得∠BOD=(180 - 2y)°,∠BOE = y°,所以∠DOE = |∠BOD - ∠BOE| = |180 - 3y|°。当∠BOE,∠BOD,∠DOE这三个角中有一个角的度数是另外一个角度数的2倍时,分类讨论如下:①若∠BOE = 2∠BOD,则y = 2(180 - 2y),解得y = 72,则∠AOB = 144°;②若∠BOE = 2∠DOE,则y = 2|180 - 3y|,解得y = $\frac{360}{7}$或72,则∠AOB = $(\frac{720}{7})$°或144°;③若∠BOD = 2∠BOE,则180 - 2y = 2y,解得y = 45,则∠AOB = 90°;④若∠BOD = 2∠DOE,则180 - 2y = |360 - 6y|,解得y = 45或 $\frac{135}{2}$,则∠AOB = 90°或135°;⑤若∠DOE = 2∠BOD,则|180 - 3y| = 2(180 - 2y),解得y = $\frac{540}{7}$,则∠AOB = $(\frac{1080}{7})$°;⑥若∠DOE = 2∠BOE,则|180 - 3y| = 2y,解得y = 36(y = 180不合题意,舍去),则∠AOB = 72°。综上所述,∠AOB的度数为144°或 $(\frac{720}{7})$°或90°或135°或 $(\frac{1080}{7})$°或72°。
(1)120° 45°
(2)设∠AOB = 2x°。因为∠AOB与∠BOD互为补角,所以∠BOD = 180° - ∠AOB=(180 - 2x)°。因为OE平分∠AOB,所以∠BOE = $\frac{1}{2}$∠AOB = x°。因为∠DOE = 30°,所以分类讨论如下:①如图①,当OE在∠BOD内部时,∠DOE = ∠BOD - ∠BOE=(180 - 3x)°,所以180 - 3x = 30,解得x = 50,所以∠AOB = 100°;②如图②,当OE在∠BOD外部时,∠DOE = ∠BOE - ∠BOD=(3x - 180)°,所以3x - 180 = 30,解得x = 70,所以∠AOB = 140°。


综上所述,∠AOB的度数为100°或140°。
(3)设∠AOB = 2y°,则同(2),得∠BOD=(180 - 2y)°,∠BOE = y°,所以∠DOE = |∠BOD - ∠BOE| = |180 - 3y|°。当∠BOE,∠BOD,∠DOE这三个角中有一个角的度数是另外一个角度数的2倍时,分类讨论如下:①若∠BOE = 2∠BOD,则y = 2(180 - 2y),解得y = 72,则∠AOB = 144°;②若∠BOE = 2∠DOE,则y = 2|180 - 3y|,解得y = $\frac{360}{7}$或72,则∠AOB = $(\frac{720}{7})$°或144°;③若∠BOD = 2∠BOE,则180 - 2y = 2y,解得y = 45,则∠AOB = 90°;④若∠BOD = 2∠DOE,则180 - 2y = |360 - 6y|,解得y = 45或 $\frac{135}{2}$,则∠AOB = 90°或135°;⑤若∠DOE = 2∠BOD,则|180 - 3y| = 2(180 - 2y),解得y = $\frac{540}{7}$,则∠AOB = $(\frac{1080}{7})$°;⑥若∠DOE = 2∠BOE,则|180 - 3y| = 2y,解得y = 36(y = 180不合题意,舍去),则∠AOB = 72°。综上所述,∠AOB的度数为144°或 $(\frac{720}{7})$°或90°或135°或 $(\frac{1080}{7})$°或72°。
4.(13分)新趋势 推导探究 如图①,将一副直角三角板摆放在直线$MN$上,在直角三角板$OAB和直角三角板OCD$中,$\angle OAB = \angle OCD = 90^{\circ}$,$\angle AOB = 45^{\circ}$,$\angle COD = 30^{\circ}$.
(1)保持直角三角板$OCD$不动,当直角三角板$OAB$旋转至图②所示位置时,$\angle BOD与\angle AON$之间有怎样的数量关系?请说明理由;
(2)如图③,若直角三角板$OAB绕点O以每秒6^{\circ}$的速度逆时针旋转,同时直角三角板$OCD也绕点O以每秒3^{\circ}$的速度逆时针旋转,当边$OB旋转至射线OM$上时,两把直角三角板同时停止转动.设旋转的时间为$t\ \unit{s}$,则在此过程中,是否存在某一时刻,使得$\angle BOD + \angle AON = 60^{\circ}$?若存在,请求出$t$的值;若不存在,请说明理由.
 视频精讲
视频精讲
(1)保持直角三角板$OCD$不动,当直角三角板$OAB$旋转至图②所示位置时,$\angle BOD与\angle AON$之间有怎样的数量关系?请说明理由;
(2)如图③,若直角三角板$OAB绕点O以每秒6^{\circ}$的速度逆时针旋转,同时直角三角板$OCD也绕点O以每秒3^{\circ}$的速度逆时针旋转,当边$OB旋转至射线OM$上时,两把直角三角板同时停止转动.设旋转的时间为$t\ \unit{s}$,则在此过程中,是否存在某一时刻,使得$\angle BOD + \angle AON = 60^{\circ}$?若存在,请求出$t$的值;若不存在,请说明理由.
 视频精讲
视频精讲答案:(1)∠BOD - ∠AON = 15°。理由如下:因为∠AOB = 45°,∠COD = 30°,所以∠BOD - ∠AON = ∠AOB + ∠AOD - (∠AOD + ∠COD)=∠AOB - ∠COD = 15°。
(2)因为∠AOB = 45°,∠COD = 30°,所以当边OB旋转至射线OM上时,t = 180÷6 = 30;当边OA旋转至射线ON上时,t = 45÷6 = $\frac{15}{2}$;当边OB与边OD重合时,t = 30÷(6 - 3)=10。若∠BOD + ∠AON = 60°,则分类讨论如下:①当0≤t≤ $\frac{15}{2}$时,∠AON=(45 - 6t)°,∠BON = 6t°,∠DON=(3t + 30)°,所以∠BOD = ∠DON - ∠BON=(30 - 3t)°,所以30 - 3t+(45 - 6t)=60,解得t = $\frac{5}{3}$;②当 $\frac{15}{2}$<t<10时,∠AON=(6t - 45)°,∠BOD=(30 - 3t)°,所以30 - 3t+(6t - 45)=60,解得t = 25,不合题意,舍去;③当10≤t≤30时,∠AON=(6t - 45)°,∠BON = 6t°,∠DON=(3t + 30)°,所以∠BOD = ∠BON - ∠DON=(3t - 30)°,所以3t - 30+(6t - 45)=60,解得t = 15。综上所述,当t = $\frac{5}{3}$或15时,∠BOD + ∠AON = 60°。
(2)因为∠AOB = 45°,∠COD = 30°,所以当边OB旋转至射线OM上时,t = 180÷6 = 30;当边OA旋转至射线ON上时,t = 45÷6 = $\frac{15}{2}$;当边OB与边OD重合时,t = 30÷(6 - 3)=10。若∠BOD + ∠AON = 60°,则分类讨论如下:①当0≤t≤ $\frac{15}{2}$时,∠AON=(45 - 6t)°,∠BON = 6t°,∠DON=(3t + 30)°,所以∠BOD = ∠DON - ∠BON=(30 - 3t)°,所以30 - 3t+(45 - 6t)=60,解得t = $\frac{5}{3}$;②当 $\frac{15}{2}$<t<10时,∠AON=(6t - 45)°,∠BOD=(30 - 3t)°,所以30 - 3t+(6t - 45)=60,解得t = 25,不合题意,舍去;③当10≤t≤30时,∠AON=(6t - 45)°,∠BON = 6t°,∠DON=(3t + 30)°,所以∠BOD = ∠BON - ∠DON=(3t - 30)°,所以3t - 30+(6t - 45)=60,解得t = 15。综上所述,当t = $\frac{5}{3}$或15时,∠BOD + ∠AON = 60°。