1. 作为世界文化遗产的长城,其总长大约为6700000m.将6700000用科学记数法表示为(
A.$6.7×10^{5}$
B.$6.7×10^{6}$
C.$0.67×10^{7}$
D.$67×10^{8}$
B
)A.$6.7×10^{5}$
B.$6.7×10^{6}$
C.$0.67×10^{7}$
D.$67×10^{8}$
答案:B
解析:
科学记数法的表示形式为$a×10^{n}$,其中$1\leq\vert a\vert<10$,$n$为整数。确定$n$的值时,要看把原数变成$a$时,小数点移动了多少位,$n$的值与小数点移动的位数相同。当原数绝对值$>1$时,$n$是正数;当原数绝对值$<1$时,$n$是负数。
将$6700000$转变为$a×10^{n}$的形式,$a=6.7$,小数点向左移动了$6$位,所以$n=6$,即$6700000=6.7×10^{6}$。
B
将$6700000$转变为$a×10^{n}$的形式,$a=6.7$,小数点向左移动了$6$位,所以$n=6$,即$6700000=6.7×10^{6}$。
B
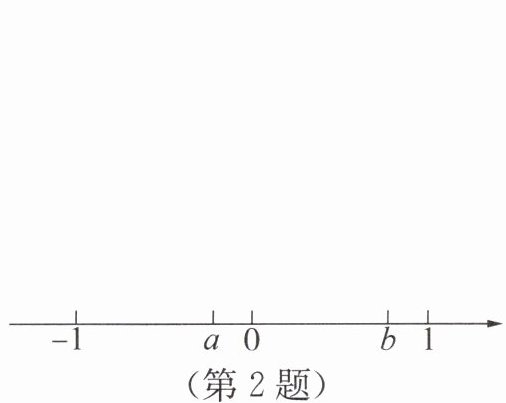
2. 若有理数a,b在数轴上的位置如图所示,则代数式$\frac {|a|}{a}+\frac {|b - 1|}{b - 1}-\frac {|a + b|}{a + b}$的值是(
A.-1
B.1
C.3
D.-3
D
)
A.-1
B.1
C.3
D.-3
答案:D
解析:
由数轴知:$a < 0$,$0 < b < 1$,$|a| < |b|$,则$a + b > 0$。
$\frac{|a|}{a} = \frac{-a}{a} = -1$;
$b - 1 < 0$,$\frac{|b - 1|}{b - 1} = \frac{1 - b}{b - 1} = -1$;
$\frac{|a + b|}{a + b} = \frac{a + b}{a + b} = 1$;
原式$= -1 + (-1) - 1 = -3$。
D
$\frac{|a|}{a} = \frac{-a}{a} = -1$;
$b - 1 < 0$,$\frac{|b - 1|}{b - 1} = \frac{1 - b}{b - 1} = -1$;
$\frac{|a + b|}{a + b} = \frac{a + b}{a + b} = 1$;
原式$= -1 + (-1) - 1 = -3$。
D
3. (2025·江苏苏州期末)如图,直线$AB// CD$,点G,F分别在AB,CD上,$GE⊥EF$.若$∠BGE = 60^{\circ}$,则$∠EFD$的度数是(

A.$60^{\circ}$
B.$30^{\circ}$
C.$40^{\circ}$
D.$70^{\circ}$
B
)
A.$60^{\circ}$
B.$30^{\circ}$
C.$40^{\circ}$
D.$70^{\circ}$
答案:B
解析:
过点E作EH//AB,
∵AB//CD,∴EH//CD,
∵∠BGE=60°,∴∠GEH=∠BGE=60°,
∵GE⊥EF,∴∠GEF=90°,
∴∠HEF=∠GEF - ∠GEH=90° - 60°=30°,
∵EH//CD,∴∠EFD=∠HEF=30°,
答案:B
∵AB//CD,∴EH//CD,
∵∠BGE=60°,∴∠GEH=∠BGE=60°,
∵GE⊥EF,∴∠GEF=90°,
∴∠HEF=∠GEF - ∠GEH=90° - 60°=30°,
∵EH//CD,∴∠EFD=∠HEF=30°,
答案:B
4. 新趋势 传统文化 我国古代数学著作《增删算法统宗》记载“绳索量竿”问题:一条竿子一条索,索比竿子长一托.折回索子却量竿,却比竿子短一托.其大意如下:现有一根竿和一条绳索,用绳索去量竿,绳索比竿长5尺;如果将绳索对半折后再去量竿,就比竿短5尺.设绳索长x尺,则可列方程为(
A.$\frac {1}{2}x= (x - 5)-5$
B.$\frac {1}{2}x= (x + 5)+5$
C.$2x= (x - 5)-5$
D.$2x= (x + 5)+5$
A
)A.$\frac {1}{2}x= (x - 5)-5$
B.$\frac {1}{2}x= (x + 5)+5$
C.$2x= (x - 5)-5$
D.$2x= (x + 5)+5$
答案:A
解析:
设绳索长$x$尺,因为绳索比竿长5尺,所以竿长为$(x - 5)$尺。
将绳索对半折后长度为$\frac{1}{2}x$尺,此时比竿短5尺,所以可列方程:$\frac{1}{2}x = (x - 5)-5$。
A
将绳索对半折后长度为$\frac{1}{2}x$尺,此时比竿短5尺,所以可列方程:$\frac{1}{2}x = (x - 5)-5$。
A
5. 某鞋店正举办开学特惠活动,如图为活动说明.小彻打算在该店同时购买一双球鞋和一双皮鞋,且他有一张购买的所有商品定价皆打八折的折价券.若小彻计算后发现使用折价券与参加特惠活动两者的花费相差50元,则下列说法正确的是(
A.使用折价券的花费较少,且两双鞋的定价相差100元
B.使用折价券的花费较少,且两双鞋的定价相差250元
C.参加特惠活动的花费较少,且两双鞋的定价相差100元
D.参加特惠活动的花费较少,且两双鞋的定价相差250元
B
)A.使用折价券的花费较少,且两双鞋的定价相差100元
B.使用折价券的花费较少,且两双鞋的定价相差250元
C.参加特惠活动的花费较少,且两双鞋的定价相差100元
D.参加特惠活动的花费较少,且两双鞋的定价相差250元
答案:B
解析:
设两双鞋的定价分别为$x$元、$y$元,且$x > y$。
特惠活动花费:$x + 0.6y$
折价券花费:$0.8(x + y)$
两者花费差:$|(x + 0.6y) - 0.8(x + y)| = 50$
化简得:$|0.2x - 0.2y| = 50$,即$0.2|x - y| = 50$,$|x - y| = 250$
比较$x + 0.6y$与$0.8(x + y)$:$x + 0.6y - 0.8x - 0.8y = 0.2x - 0.2y = 0.2(x - y) > 0$,故折价券花费较少。
两双鞋定价相差250元。
B
特惠活动花费:$x + 0.6y$
折价券花费:$0.8(x + y)$
两者花费差:$|(x + 0.6y) - 0.8(x + y)| = 50$
化简得:$|0.2x - 0.2y| = 50$,即$0.2|x - y| = 50$,$|x - y| = 250$
比较$x + 0.6y$与$0.8(x + y)$:$x + 0.6y - 0.8x - 0.8y = 0.2x - 0.2y = 0.2(x - y) > 0$,故折价券花费较少。
两双鞋定价相差250元。
B