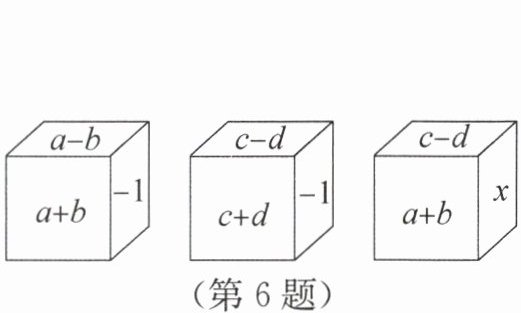
6. 亮点原创 一个正方体纸盒的六个面上填有不同的数或式,从不同方向看到的情形如图所示.若相对两个面上的数或式的值互为相反数,则$(a + c - x)^{2025}$的值为(
A.1
B.-1
C.$2^{2025}$
D.2025
B
)
A.1
B.-1
C.$2^{2025}$
D.2025
答案:B 解析:结合题图可知:“a+b”与“c+d”所在的面相对;“c-d”与“a-b”所在的面相对;“x”与“−1”所在的面相对.因为相对两个面上的数或式的值互为相反数,所以a+b+(c+d)=0①,c-d+(a-b)=0②,且x+(−1)=0,所以x=1.由①+②,得2(a+c)=0,所以a+c=0,所以(a+c−x)²⁰²⁵=(−1)²⁰²⁵=−1.
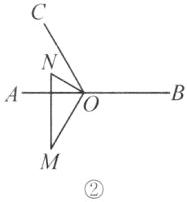
7. 新素养 几何直观 已知点O在直线AB上,过点O作射线OC,$∠BOC = 120^{\circ}$,一直角三角板的直角顶点与点O重合,边OM与射线OB重合,边ON在直线AB下方(如图①).若三角板以每秒$10^{\circ}$的速度绕点O逆时针旋转一周(如图②),设旋转的时间为ts,则在旋转的过程中,当直线ON恰好平分$∠AOC$时,t的值为( )

A.5
B.6
C.5或23
D.6或24

A.5
B.6
C.5或23
D.6或24
答案:
D 解析:因为∠BOC=120°,所以∠AOC=180°−∠BOC=60°,因为∠MON=90°,直线ON平分∠AOC,所以分类讨论如下:①如图①,当ON在直线AB下方时,∠BON=$\frac{1}{2}$∠AOC=30°,所以∠BOM=∠MON−∠BON=60°,所以t=60÷10=6;②如图②,当ON在直线AB上方时,t=6+180÷10=24.综上所述,当直线ON恰好平分∠AOC时,t的值为6或24.

D 解析:因为∠BOC=120°,所以∠AOC=180°−∠BOC=60°,因为∠MON=90°,直线ON平分∠AOC,所以分类讨论如下:①如图①,当ON在直线AB下方时,∠BON=$\frac{1}{2}$∠AOC=30°,所以∠BOM=∠MON−∠BON=60°,所以t=60÷10=6;②如图②,当ON在直线AB上方时,t=6+180÷10=24.综上所述,当直线ON恰好平分∠AOC时,t的值为6或24.


8. 新趋势 开放探究 (2024·湖北)写出一个大于-1的数:
0(答案不唯一)
.答案:0(答案不唯一)
9. 若一个角比它的补角少$40^{\circ}$,则这个角余角的度数为
20°
.答案:20°
解析:
设这个角的度数为$x$,则它的补角为$180^{\circ}-x$。
由题意得:$x = (180^{\circ}-x) - 40^{\circ}$
解得:$x = 70^{\circ}$
这个角的余角为$90^{\circ}-70^{\circ}=20^{\circ}$
20°
由题意得:$x = (180^{\circ}-x) - 40^{\circ}$
解得:$x = 70^{\circ}$
这个角的余角为$90^{\circ}-70^{\circ}=20^{\circ}$
20°
10. 若当$x = 1$时,多项式$mx^{3}-nx + 5$的值为-2025,则当$x = - 1$时,多项式$mx^{3}-nx + 5$的值为
2035
.答案:2035
解析:
当$x = 1$时,代入多项式$mx^{3}-nx + 5$得:$m×1^{3}-n×1 + 5 = m - n + 5$,已知此时值为$-2025$,则$m - n + 5=-2025$,可得$m - n=-2030$。
当$x=-1$时,多项式为$m×(-1)^{3}-n×(-1)+5=-m + n + 5$,而$-m + n=-(m - n)=2030$,所以$-m + n + 5=2030 + 5=2035$。
2035
当$x=-1$时,多项式为$m×(-1)^{3}-n×(-1)+5=-m + n + 5$,而$-m + n=-(m - n)=2030$,所以$-m + n + 5=2030 + 5=2035$。
2035
11. 有两个相同的长方体纸盒,它们的长、宽、高分别是12cm,6cm,2cm,现要用这两个纸盒搭成一个大长方体,则搭成的大长方体的表面积最小为
288
$cm^{2}$.答案:288
解析:
两个相同长方体的表面积之和:$2×2×(12×6 + 12×2 + 6×2)=2×2×(72 + 24 + 12)=2×2×108=432\,\text{cm}^2$
要使大长方体表面积最小,需将最大面重合,最大面面积:$12×6 = 72\,\text{cm}^2$
重合后减少的表面积:$2×72 = 144\,\text{cm}^2$
大长方体表面积最小为:$432 - 144 = 288\,\text{cm}^2$
288
要使大长方体表面积最小,需将最大面重合,最大面面积:$12×6 = 72\,\text{cm}^2$
重合后减少的表面积:$2×72 = 144\,\text{cm}^2$
大长方体表面积最小为:$432 - 144 = 288\,\text{cm}^2$
288
12. (2025·江苏无锡期末)已知关于x的方程$\frac {x + 3}{3}-\frac {mx - 1}{6}= -1$的解为整数,则所有符合条件的正整数m的值之和为
19
.答案:19
解析:
解方程$\frac{x + 3}{3}-\frac{mx - 1}{6}= -1$:
去分母,得$2(x + 3)-(mx - 1)= -6$
去括号,得$2x + 6 - mx + 1= -6$
移项、合并同类项,得$(2 - m)x= -13$
解得$x=\frac{13}{m - 2}$
因为方程的解为整数,$m$为正整数,所以$m - 2$是13的正因数或负因数。
13的因数为$\pm1,\pm13$,则:
当$m - 2=1$时,$m=3$,$x=13$
当$m - 2=13$时,$m=15$,$x=1$
当$m - 2=-1$时,$m=1$,$x=-13$
当$m - 2=-13$时,$m=-11$(舍去,非正整数)
符合条件的正整数$m$为1,3,15,其和为$1 + 3 + 15=19$
19
去分母,得$2(x + 3)-(mx - 1)= -6$
去括号,得$2x + 6 - mx + 1= -6$
移项、合并同类项,得$(2 - m)x= -13$
解得$x=\frac{13}{m - 2}$
因为方程的解为整数,$m$为正整数,所以$m - 2$是13的正因数或负因数。
13的因数为$\pm1,\pm13$,则:
当$m - 2=1$时,$m=3$,$x=13$
当$m - 2=13$时,$m=15$,$x=1$
当$m - 2=-1$时,$m=1$,$x=-13$
当$m - 2=-13$时,$m=-11$(舍去,非正整数)
符合条件的正整数$m$为1,3,15,其和为$1 + 3 + 15=19$
19
13. 如图,在无限大的正方形网格中按规律涂上阴影,图①②③中阴影部分小正方形的个数分别为5,9,15.根据此规律,图⑳中阴影部分小正方形的个数是____.


423
答案:423 解析:因为题图①中阴影部分小正方形有1×2+3=5(个),题图②中阴影部分小正方形有2×3+3=9(个),题图③中阴影部分小正方形有3×4+3=15(个),...,所以依此规律,图⑳中阴影部分小正方形有20×21+3=423(个).
14. 如图,已知$∠AOB = 90^{\circ}$,$∠COD在∠AOB$内部,且$∠COD = 45^{\circ}$.给出下列说法:①若$∠AOC = ∠BOD$,则图中有2对互余的角;②若OE平分$∠BOC$,则$∠AOC = 2∠DOE$;③若OM平分$∠AOC$,ON在$∠AOB$内部,且$∠MON = 45^{\circ}$,则OD平分$∠BON$;④若在$∠AOB外部分别作∠AOC$,$∠BOD的余角∠AOP$,$∠BOQ$,则$\frac {∠AOP + ∠BOQ}{∠COD}= 3$.其中正确的是____.(填序号)
②④
答案:②④ 解析:因为∠AOB=90°,∠COD在∠AOB内部,所以∠AOC+∠BOC=90°,∠AOD+∠BOD=90°.若∠AOC=∠BOD,则∠BOD+∠BOC=90°,∠AOD+∠AOC=90°,所以题图中有4对互余的角,故①错误;设∠AOC=x°,则∠BOC=∠AOB−∠AOC=(90−x)°.因为∠COD=45°,所以∠BOD=∠BOC−∠COD=(45−x)°.若OE平分∠BOC,则∠BOE=$\frac{1}{2}$∠BOC=(45−$\frac{1}{2}$x)°,所以∠DOE=∠BOE−∠BOD=$\frac{1}{2}$x°,所以∠AOC=2∠DOE,故②正确;若OM平分∠AOC,则∠COM=$\frac{1}{2}$∠AOC=$\frac{1}{2}$x°.因为∠MON=45°,所以∠CON=∠MON−∠COM=(45−$\frac{1}{2}$x)°,所以∠DON=∠COD−∠CON=$\frac{1}{2}$x°,所以若OD平分∠BON,则∠BOD=∠DON,即45−x=$\frac{1}{2}$x,解得x=30,即当∠AOC=30°时,OD平分∠BON,故③错误;因为∠AOP=90°−∠AOC=(90−x)°,∠BOQ=90°−∠BOD=(45+x)°,所以∠AOP+∠BOQ=135°,所以$\frac{∠AOP + ∠BOQ}{∠COD}$=3,故④正确.