15. (14分)已知多项式$M = - 4mn + m^{2}$,$N = - mn + 3m^{2}-n^{2}$,且多项式P与$M - N的和为-3n^{2}-mn$.
(1)求多项式P;
(2)若$|m + 1|与(n - 2)^{2}$互为相反数,求多项式P的值.
(1)求多项式P;
(2)若$|m + 1|与(n - 2)^{2}$互为相反数,求多项式P的值.
答案:(1)因为M=−4mn+m²,N=−mn+3m²−n²,所以M−N=−4mn+m²−(−mn+3m²−n²)=−3mn−2m²+n².因为多项式P与M−N的和为−3n²−mn,所以P=−3n²−mn−(−3mn−2m²+n²)=−4n²+2mn+2m².
(2)因为|m+1|与(n−2)²互为相反数,所以|m+1|+(n−2)²=0.因为|m+1|≥0,(n−2)²≥0,所以m+1=0,n−2=0,所以m=−1,n=2,所以P=−4n²+2mn+2m²=−4×2²+2×(−1)×2+2×(−1)²=−18.
(2)因为|m+1|与(n−2)²互为相反数,所以|m+1|+(n−2)²=0.因为|m+1|≥0,(n−2)²≥0,所以m+1=0,n−2=0,所以m=−1,n=2,所以P=−4n²+2mn+2m²=−4×2²+2×(−1)×2+2×(−1)²=−18.
16. (2025·江苏南京期末·14分)$|4 - 1|$表示4和1的差的绝对值,也可以理解为数轴上表示4和1的两点之间的距离;$|4 + 1|可以看作|4-(-1)|$,表示4和-1的差的绝对值,也可以理解为数轴上表示4和-1的两点之间的距离.根据以上信息,解答下列问题:
(1)计算:$|4-(-1)|= $
(2)计算:$|5 + 2|= $
(3)利用数轴找出所有符合条件的整数x,使得$|x + 3| = 5$,则x=
(4)利用数轴找出所有符合条件的整数x,使得$|x + 3|+|x - 2| = 5$,这样的整数x有几个?
(1)计算:$|4-(-1)|= $
5
;(2)计算:$|5 + 2|= $
7
;(3)利用数轴找出所有符合条件的整数x,使得$|x + 3| = 5$,则x=
2或−8
;(4)利用数轴找出所有符合条件的整数x,使得$|x + 3|+|x - 2| = 5$,这样的整数x有几个?
由题意,得数轴上表示−3和2的两点之间的距离为|−3−2|=5.因为|x+3|+|x−2|=5,所以数轴上表示x的点到表示−3和2的两点的距离之和为5,所以x可取−3,−2,−1,0,1,2,所以这样的整数x有6个.
答案:(1)5 (2)7 (3)2或−8
(4)由题意,得数轴上表示−3和2的两点之间的距离为|−3−2|=5.因为|x+3|+|x−2|=5,所以数轴上表示x的点到表示−3和2的两点的距离之和为5,所以x可取−3,−2,−1,0,1,2,所以这样的整数x有6个.
(4)由题意,得数轴上表示−3和2的两点之间的距离为|−3−2|=5.因为|x+3|+|x−2|=5,所以数轴上表示x的点到表示−3和2的两点的距离之和为5,所以x可取−3,−2,−1,0,1,2,所以这样的整数x有6个.
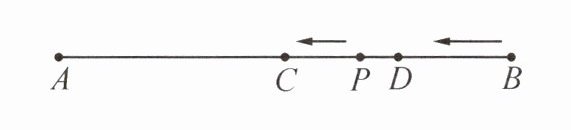
17. (16分)新素养 推理能力 如图,P是线段AB上任意一点,$AB = 12cm$,C,D两点分别从P,B两点同时出发向点A运动,且点C的运动速度为2cm/s,点D的运动速度为3cm/s,设运动的时间为ts.
(1)已知$AP = 8cm$.
①当$t = 1$时,求CD的长;
②当点D在线段PB上运动时,试说明:$AC = 2CD$;
(2)若当$t = 2$时,$CD = 1cm$,求AP的长.
(1)已知$AP = 8cm$.
①当$t = 1$时,求CD的长;
②当点D在线段PB上运动时,试说明:$AC = 2CD$;
(2)若当$t = 2$时,$CD = 1cm$,求AP的长.

答案:(1)①当t=1时,CP=2×1=2(cm),DB=3×1=3(cm).因为AB=12cm,AP=8cm,所以CD=AB−AP+CP−DB=3cm.
②由题意,得CP=2tcm,DB=3tcm.因为AB=12cm,AP=8cm,所以CD=AB−AP+CP−DB=(4−t)cm,AC=AP−CP=(8−2t)cm,所以AC=2CD.
(2)当t=2时,CP=4cm,DB=6cm.因为AB=12cm,所以AD=AB−DB=6cm.分类讨论如下:若点C在点D左侧,则AC=AD−CD=6−1=5(cm),所以AP=AC+CP=9cm;若点C在点D右侧,则AC=AD+CD=6+1=7(cm),所以AP=AC+CP=11cm.综上所述,AP的长为9cm或11cm.
②由题意,得CP=2tcm,DB=3tcm.因为AB=12cm,AP=8cm,所以CD=AB−AP+CP−DB=(4−t)cm,AC=AP−CP=(8−2t)cm,所以AC=2CD.
(2)当t=2时,CP=4cm,DB=6cm.因为AB=12cm,所以AD=AB−DB=6cm.分类讨论如下:若点C在点D左侧,则AC=AD−CD=6−1=5(cm),所以AP=AC+CP=9cm;若点C在点D右侧,则AC=AD+CD=6+1=7(cm),所以AP=AC+CP=11cm.综上所述,AP的长为9cm或11cm.