1. 云南省矿产资源极为丰富,被誉为“有色金属王国”.锂资源方面,滇中地区被中国科学院地球化学研究所探明拥有氧化锂资源达340 000 t.将340 000用科学记数法表示为 (
A.$ 340×10^{4} $
B.$ 34×10^{5} $
C.$ 3.4×10^{5} $
D.$ 0.34×10^{6} $
C
)A.$ 340×10^{4} $
B.$ 34×10^{5} $
C.$ 3.4×10^{5} $
D.$ 0.34×10^{6} $
答案:C
解析:
科学记数法的表示形式为$a×10^{n}$,其中$1\leq\vert a\vert\lt10$,$n$为整数。确定$n$的值时,要看把原数变成$a$时,小数点移动了多少位,$n$的值与小数点移动的位数相同。当原数绝对值$\gt1$时,$n$是正数;当原数绝对值$\lt1$时,$n$是负数。
将$340000$转变为$a×10^{n}$的形式,$a=3.4$,小数点向左移动了$5$位,所以$n=5$,即$340000=3.4×10^{5}$。
C
将$340000$转变为$a×10^{n}$的形式,$a=3.4$,小数点向左移动了$5$位,所以$n=5$,即$340000=3.4×10^{5}$。
C
2. 已知有理数a,b满足$ a>b $,则下列结论一定正确的是 (
A.$ |a|>|b| $
B.$ \frac{1}{a}>\frac{1}{b} $
C.$ a^{2}>b^{2} $
D.$ a^{3}>b^{3} $
D
)A.$ |a|>|b| $
B.$ \frac{1}{a}>\frac{1}{b} $
C.$ a^{2}>b^{2} $
D.$ a^{3}>b^{3} $
答案:D
解析:
A. 当$a=1$,$b=-2$时,$a > b$,但$|a|=1$,$|b|=2$,$|a| < |b|$,故A错误;
B. 当$a=2$,$b=1$时,$a > b$,但$\frac{1}{a}=\frac{1}{2}$,$\frac{1}{b}=1$,$\frac{1}{a} < \frac{1}{b}$,故B错误;
C. 当$a=1$,$b=-2$时,$a > b$,但$a^2=1$,$b^2=4$,$a^2 < b^2$,故C错误;
D. 对于有理数$a$,$b$,若$a > b$,则$a^3 - b^3=(a - b)(a^2 + ab + b^2)$,因为$a > b$,所以$a - b > 0$,又$a^2 + ab + b^2=(a + \frac{b}{2})^2 + \frac{3b^2}{4} \geq 0$,且仅当$a = b = 0$时等号成立,而$a > b$,所以$a^2 + ab + b^2 > 0$,则$a^3 - b^3 > 0$,即$a^3 > b^3$,故D正确。
D
B. 当$a=2$,$b=1$时,$a > b$,但$\frac{1}{a}=\frac{1}{2}$,$\frac{1}{b}=1$,$\frac{1}{a} < \frac{1}{b}$,故B错误;
C. 当$a=1$,$b=-2$时,$a > b$,但$a^2=1$,$b^2=4$,$a^2 < b^2$,故C错误;
D. 对于有理数$a$,$b$,若$a > b$,则$a^3 - b^3=(a - b)(a^2 + ab + b^2)$,因为$a > b$,所以$a - b > 0$,又$a^2 + ab + b^2=(a + \frac{b}{2})^2 + \frac{3b^2}{4} \geq 0$,且仅当$a = b = 0$时等号成立,而$a > b$,所以$a^2 + ab + b^2 > 0$,则$a^3 - b^3 > 0$,即$a^3 > b^3$,故D正确。
D
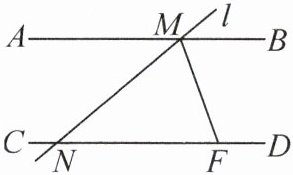
3. 如图,直线$ AB// CD $,直线l分别交AB,CD于点M,N,$ ∠BMN $的平分线交CD于点F.若$ ∠MNF= 40^{\circ} $,则$ ∠DFM $的度数为 (
A.$ 70^{\circ} $
B.$ 110^{\circ} $
C.$ 120^{\circ} $
D.$ 140^{\circ} $
B
) 
A.$ 70^{\circ} $
B.$ 110^{\circ} $
C.$ 120^{\circ} $
D.$ 140^{\circ} $
答案:B
解析:
∵AB//CD,
∴∠BMN + ∠MNF = 180°(两直线平行,同旁内角互补)。
∵∠MNF = 40°,
∴∠BMN = 180° - 40° = 140°。
∵MF平分∠BMN,
∴∠BMF = ∠NMF = 140°÷2 = 70°。
∵AB//CD,
∴∠MFN = ∠BMF = 70°(两直线平行,内错角相等)。
∵∠MFN + ∠DFM = 180°(平角定义),
∴∠DFM = 180° - 70° = 110°。
B
∴∠BMN + ∠MNF = 180°(两直线平行,同旁内角互补)。
∵∠MNF = 40°,
∴∠BMN = 180° - 40° = 140°。
∵MF平分∠BMN,
∴∠BMF = ∠NMF = 140°÷2 = 70°。
∵AB//CD,
∴∠MFN = ∠BMF = 70°(两直线平行,内错角相等)。
∵∠MFN + ∠DFM = 180°(平角定义),
∴∠DFM = 180° - 70° = 110°。
B
4. (2025·江苏连云港期末)观察依次排列的一列单项式:$ x,-2x^{2},4x^{3},-8x^{4},16x^{5},… $,按你发现的规律继续写下去,第8个单项式是 (
A.$ -128x^{7} $
B.$ -128x^{8} $
C.$ -256x^{7} $
D.$ -256x^{8} $
B
)A.$ -128x^{7} $
B.$ -128x^{8} $
C.$ -256x^{7} $
D.$ -256x^{8} $
答案:B
解析:
系数规律:$(-2)^{n-1}$;
指数规律:$x^n$;
第8个单项式:$(-2)^{8-1}x^8=-128x^8$。
B
指数规律:$x^n$;
第8个单项式:$(-2)^{8-1}x^8=-128x^8$。
B
5. 某校争取到一项植树任务,领到一批树苗后,按下列方法依次由各班领取:一班领取全部的$ \frac{1}{10} $,二班领取100棵和余下的$ \frac{1}{10} $,三班领取200棵和余下的$ \frac{1}{10} $,四班领取300棵和余下的$ \frac{1}{10} $,…,最后树苗全部被领完,且各班领取的树苗数量相同,则树苗总棵数为 (
A.6 400
B.8 100
C.9 000
D.4 900
C
)A.6 400
B.8 100
C.9 000
D.4 900
答案:C
解析:
设树苗总棵数为$x$。
一班领取$\frac{1}{10}x$棵。
二班领取$100 + \frac{1}{10}(x - \frac{1}{10}x - 100) = 100 + \frac{1}{10}(\frac{9}{10}x - 100) = 90 + \frac{9}{100}x$棵。
由各班领取数量相同,得$\frac{1}{10}x = 90 + \frac{9}{100}x$。
解得$x = 9000$。
C
一班领取$\frac{1}{10}x$棵。
二班领取$100 + \frac{1}{10}(x - \frac{1}{10}x - 100) = 100 + \frac{1}{10}(\frac{9}{10}x - 100) = 90 + \frac{9}{100}x$棵。
由各班领取数量相同,得$\frac{1}{10}x = 90 + \frac{9}{100}x$。
解得$x = 9000$。
C
6. 新素养推理能力如图,正方形的边长均是a,以图①②③呈现的规律类推,图⑩中阴影部分的面积是 (
A.$ πa^{2} $
B.$ \frac{2-π}{2}a^{2} $
C.$ \frac{4-π}{4}a^{2} $
D.$ \frac{π-1}{4}a^{2} $
C
)A.$ πa^{2} $
B.$ \frac{2-π}{2}a^{2} $
C.$ \frac{4-π}{4}a^{2} $
D.$ \frac{π-1}{4}a^{2} $
答案:C 解析:由题图①②③呈现的规律,得图⑩中有$10^{2}=100$(个)圆,且每个圆的半径是$\frac{a}{20}$,所以这100个圆的总面积是$\pi(\frac{a}{20})^{2}×100=\frac{\pi a^{2}}{4}$。因为正方形的面积是$a^{2}$,所以图中阴影部分的面积是$a^{2}-\frac{\pi a^{2}}{4}=\frac{4 - \pi}{4}a^{2}$。
7. 在线段AB上有3种点,第1种是将线段AB平分的点,第2种是将线段AB五等分的点,第3种是将线段AB十等分的点,则这些点连同线段AB的端点可组成的线段条数是 (
A.36
B.45
C.55
D.78
C
)A.36
B.45
C.55
D.78
答案:C 解析:由题意,得线段AB上(包含A,B两点)共有$1 + 4 + 9 - 5 + 2 = 11$(个)点,所以可组成的线段条数是$\frac{10×11}{2}=55$。