8.(3分)已知$m与n$互为相反数,且$m与n$在数轴上对应的点之间的距离为6.若$m\lt n$,则$m= $
-3
.答案:-3
解析:
因为$m$与$n$互为相反数,所以$n = -m$。
又因为$m$与$n$在数轴上对应的点之间的距离为$6$,且$m\lt n$,所以$n - m=6$。
将$n = -m$代入$n - m=6$,得$-m - m=6$,即$-2m = 6$,解得$m=-3$。
$-3$
又因为$m$与$n$在数轴上对应的点之间的距离为$6$,且$m\lt n$,所以$n - m=6$。
将$n = -m$代入$n - m=6$,得$-m - m=6$,即$-2m = 6$,解得$m=-3$。
$-3$
9.(3分)新素养 抽象能力 用“$\Rightarrow$”与“$\Leftarrow$”表示一种计算法则:$a\Rightarrow b= -b$,$a\Leftarrow b= -a$,如$2\Rightarrow3= -3$,则$(2024\Rightarrow2025)\Leftarrow(2023\Rightarrow2022)= $______
2025
.答案:2025
解析:
$2024\Rightarrow2025=-2025$,$2023\Rightarrow2022=-2022$,$(-2025)\Leftarrow(-2022)=2025$
10.(6分)已知数$a$表示的点在数轴上的位置如图所示.
(1)在数轴上标出数$a$的相反数表示的点;
(2)若数$a表示的点与数a$的相反数表示的点相距20个单位长度,求$a$的值;
(3)在(2)的条件下,若数$b表示的点与数a$的相反数表示的点相距5个单位长度,求$b$的值.
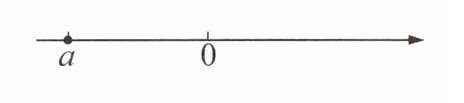
(1)在数轴上标出数$a$的相反数表示的点;
(2)若数$a表示的点与数a$的相反数表示的点相距20个单位长度,求$a$的值;
(3)在(2)的条件下,若数$b表示的点与数a$的相反数表示的点相距5个单位长度,求$b$的值.
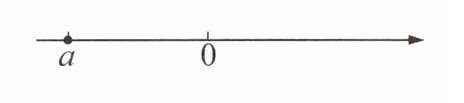
答案:(1)图略.
(2)因为数a表示的点与数a的相反数表示的点相距 20 个单位长度,所以数a表示的点距原点相距 20 个单位长度,所以数a表示的点距原点20÷2=10(个)单位长度. 又数a表示的点在原点的左边,所以a=-10.
(3)因为数b表示的点与数-10 的相反数表示的点相距5个单位长度,所以数b表示的点与数 10 表示的点相距5个单位长度. 分类讨论如下:① 当数b表示的点在数 10 表示的点的右侧时,b=10+5=15;② 当数b表示的点在数10 表示的点的左侧时,b=10-5=5. 综上所述,b的值为 15 或 5.
(2)因为数a表示的点与数a的相反数表示的点相距 20 个单位长度,所以数a表示的点距原点相距 20 个单位长度,所以数a表示的点距原点20÷2=10(个)单位长度. 又数a表示的点在原点的左边,所以a=-10.
(3)因为数b表示的点与数-10 的相反数表示的点相距5个单位长度,所以数b表示的点与数 10 表示的点相距5个单位长度. 分类讨论如下:① 当数b表示的点在数 10 表示的点的右侧时,b=10+5=15;② 当数b表示的点在数10 表示的点的左侧时,b=10-5=5. 综上所述,b的值为 15 或 5.
11.(3分)上分点三 下列说法正确的是 (
A.$|x|\lt x$
B.若$|x-1|+2$取最小值,则$x= 0$
C.若$x>1>y>-1$,则$|x|\lt|y|$
D.若$|x+1|\leqslant0$,则$x= -1$
D
)A.$|x|\lt x$
B.若$|x-1|+2$取最小值,则$x= 0$
C.若$x>1>y>-1$,则$|x|\lt|y|$
D.若$|x+1|\leqslant0$,则$x= -1$
答案:D
解析:
A. 当$x\geq0$时,$|x|=x$,则$|x|\lt x$不成立;当$x\lt0$时,$|x|=-x\gt0\gt x$,$|x|\lt x$也不成立,故A错误。
B. 因为$|x - 1|\geq0$,所以$|x - 1| + 2\geq2$,当$|x - 1|=0$,即$x=1$时取最小值,故B错误。
C. 设$x=2$,$y=0.5$,满足$x>1>y>-1$,此时$|x|=2$,$|y|=0.5$,$|x|>|y|$,故C错误。
D. 因为$|x + 1|\leq0$,且绝对值具有非负性,即$|x + 1|\geq0$,所以$|x + 1|=0$,则$x + 1=0$,解得$x=-1$,故D正确。
D
B. 因为$|x - 1|\geq0$,所以$|x - 1| + 2\geq2$,当$|x - 1|=0$,即$x=1$时取最小值,故B错误。
C. 设$x=2$,$y=0.5$,满足$x>1>y>-1$,此时$|x|=2$,$|y|=0.5$,$|x|>|y|$,故C错误。
D. 因为$|x + 1|\leq0$,且绝对值具有非负性,即$|x + 1|\geq0$,所以$|x + 1|=0$,则$x + 1=0$,解得$x=-1$,故D正确。
D
12.(3分)上分点四 已知有理数$a,b$在数轴上的位置如图所示,则下列结论错误的是 (

A.$-b\lt a<-1$
B.$1<-a\lt b$
C.$1<|a|\lt b$
D.$|a|<1<|b|$
D
)
A.$-b\lt a<-1$
B.$1<-a\lt b$
C.$1<|a|\lt b$
D.$|a|<1<|b|$
答案:D
解析:
由数轴可知:$a < -1 < 0 < 1 < b$,且$|a| < b$。
A. $-b < a < -1$,正确。
B. $1 < -a < b$,正确。
C. $1 < |a| < b$,正确。
D. $|a| < 1 < |b|$,错误。
D
A. $-b < a < -1$,正确。
B. $1 < -a < b$,正确。
C. $1 < |a| < b$,正确。
D. $|a| < 1 < |b|$,错误。
D
13.(3分)在$-2025,-2024,-2023,-2022$这4个数中,最小的是
-2025
.答案:-2025
14.(3分)若四个非零数$a,b,c,d满足|a|= -a$,$|b|= b$,$|c|= -c$,$|d|= -d$,且$|a|>|b|>|c|>|d|$,则$a,b,c,d$之间的大小关系是
a<c<d<b
.(用“$<$”号连接)答案:a<c<d<b
解析:
由$|a|=-a$,$|c|=-c$,$|d|=-d$可得$a$,$c$,$d$为负数;由$|b|=b$可得$b$为正数。
因为负数的绝对值越大,该负数越小,且$|a|>|c|>|d|$,所以$a<c<d$。
又因为正数大于负数,所以$d<b$。
综上,$a<c<d<b$。
$a<c<d<b$
因为负数的绝对值越大,该负数越小,且$|a|>|c|>|d|$,所以$a<c<d$。
又因为正数大于负数,所以$d<b$。
综上,$a<c<d<b$。
$a<c<d<b$
15.(5分)已知$|x|= 2$,$|y|= 3$,$|z|= 4$,且$x>y>z$,求$x,y,z$的值.
答案:因为|x|=2,|y|=3,|z|=4,所以x=±2,y=±3,z=±4. 因为x>y>z,所以x=2,y=-3,z=-4 或x=-2,y=-3,z=-4.
解析:
因为$|x| = 2$,所以$x = \pm 2$;因为$|y| = 3$,所以$y = \pm 3$;因为$|z| = 4$,所以$z = \pm 4$。
由于$x > y > z$,分析可能情况:
若$x = 2$,则$y$需小于$2$,$y$只能为$-3$;此时$z$需小于$-3$,$z$只能为$-4$,即$x = 2$,$y = -3$,$z = -4$。
若$x = -2$,则$y$需小于$-2$,$y$只能为$-3$;此时$z$需小于$-3$,$z$只能为$-4$,即$x = -2$,$y = -3$,$z = -4$。
综上,$x = 2$,$y = -3$,$z = -4$或$x = -2$,$y = -3$,$z = -4$。
由于$x > y > z$,分析可能情况:
若$x = 2$,则$y$需小于$2$,$y$只能为$-3$;此时$z$需小于$-3$,$z$只能为$-4$,即$x = 2$,$y = -3$,$z = -4$。
若$x = -2$,则$y$需小于$-2$,$y$只能为$-3$;此时$z$需小于$-3$,$z$只能为$-4$,即$x = -2$,$y = -3$,$z = -4$。
综上,$x = 2$,$y = -3$,$z = -4$或$x = -2$,$y = -3$,$z = -4$。