典例1 (1)小华用20元钱购买了x支单价为5元的铅笔;
(2)某班女生人数与全班总人数的比为12:25,该班女生有12y人,男生有26人。
(2)某班女生人数与全班总人数的比为12:25,该班女生有12y人,男生有26人。
答案:【解析】:
(1) 对于第一个问题,主要考查的是如何根据实际问题建立等式。题目描述了小华用20元钱购买了x支单价为5元的铅笔。根据这个描述,我们可以理解到铅笔的单价是5元,数量是x,所以总价就是5x。而题目又告诉我们总价是20元,所以我们可以得到等式$5x = 20$。
(2) 对于第二个问题,也是考查如何根据实际问题建立等式。题目描述了某班女生人数与全班总人数的比为12:25,且该班女生有12y人,男生有26人。根据这个描述,我们可以理解到全班总人数可以表示为25y(因为女生人数与全班人数的比为12:25,所以全班人数是女生人数的25/12倍,即25y),而男生人数是26人。所以我们可以得到等式$25y - 12y = 26$,表示全班人数减去女生人数等于男生人数。
【答案】:
(1) $5x = 20$
(2) $25y - 12y = 26$
(1) 对于第一个问题,主要考查的是如何根据实际问题建立等式。题目描述了小华用20元钱购买了x支单价为5元的铅笔。根据这个描述,我们可以理解到铅笔的单价是5元,数量是x,所以总价就是5x。而题目又告诉我们总价是20元,所以我们可以得到等式$5x = 20$。
(2) 对于第二个问题,也是考查如何根据实际问题建立等式。题目描述了某班女生人数与全班总人数的比为12:25,且该班女生有12y人,男生有26人。根据这个描述,我们可以理解到全班总人数可以表示为25y(因为女生人数与全班人数的比为12:25,所以全班人数是女生人数的25/12倍,即25y),而男生人数是26人。所以我们可以得到等式$25y - 12y = 26$,表示全班人数减去女生人数等于男生人数。
【答案】:
(1) $5x = 20$
(2) $25y - 12y = 26$
【变式1】根据下列情境中的等量关系列出一个等式:
(1)根据江苏省第七次全国人口普查结果,江苏省常住人口为84748016人,0~14岁人口为n人,占15.21%;
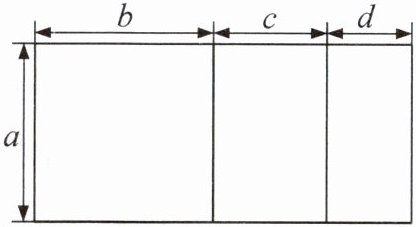
(2)如图,一张长方形纸片被分割成三部分。
(1)根据江苏省第七次全国人口普查结果,江苏省常住人口为84748016人,0~14岁人口为n人,占15.21%;
(2)如图,一张长方形纸片被分割成三部分。

答案:(1)$\frac{n}{84748016}=15.21\%$.(2)$a(b+c+d)=ab+ac+ad$.
典例2 已知等式$ax+c= ay+c$,则下列等式不一定成立的是 (
A.$ax= ay$
B.$x= y$
C.$m-ax= m-ay$
D.$2ax= 2ay$
B
)A.$ax= ay$
B.$x= y$
C.$m-ax= m-ay$
D.$2ax= 2ay$
答案:【解析】:本题主要考察等式的基本性质和运算规则。
首先,我们从原等式$ax+c=ay+c$出发,两边同时减去c,可以得到$ax=ay$,这说明选项A是成立的,因此A选项不符合题意。
接着,我们考虑选项B,$x=y$。这个等式并非在所有情况下都成立。特别地,当$a=0$时,无论x和y取何值,等式$ax=ay$都成立,但x和y本身可以不相等。因此,B选项符合题意,即$x=y$不一定成立。
对于选项C,$m-ax=m-ay$,我们可以在等式$ax=ay$的两边同时乘以-1,得到$-ax=-ay$,然后再同时加上m,即可得到$m-ax=m-ay$。所以C选项是成立的,不符合题意。
对于选项D,$2ax=2ay$,我们只需在等式$ax=ay$的两边同时乘以2,即可得到$2ax=2ay$。所以D选项也是成立的,不符合题意。
综上所述,我们可以确定答案为B,即$x=y$不一定成立。
【答案】:B
首先,我们从原等式$ax+c=ay+c$出发,两边同时减去c,可以得到$ax=ay$,这说明选项A是成立的,因此A选项不符合题意。
接着,我们考虑选项B,$x=y$。这个等式并非在所有情况下都成立。特别地,当$a=0$时,无论x和y取何值,等式$ax=ay$都成立,但x和y本身可以不相等。因此,B选项符合题意,即$x=y$不一定成立。
对于选项C,$m-ax=m-ay$,我们可以在等式$ax=ay$的两边同时乘以-1,得到$-ax=-ay$,然后再同时加上m,即可得到$m-ax=m-ay$。所以C选项是成立的,不符合题意。
对于选项D,$2ax=2ay$,我们只需在等式$ax=ay$的两边同时乘以2,即可得到$2ax=2ay$。所以D选项也是成立的,不符合题意。
综上所述,我们可以确定答案为B,即$x=y$不一定成立。
【答案】:B
【变式2】已知等式$2m= 3n$,则下列变形正确的是 (
A.$4m= 9n$
B.$2m-3= 3n+2$
C.$2m+3= 3n+3$
D.$m= \frac {2}{3}n$
C
)A.$4m= 9n$
B.$2m-3= 3n+2$
C.$2m+3= 3n+3$
D.$m= \frac {2}{3}n$
答案:C
解析:
对于选项A:等式$2m = 3n$两边同时乘以2,得$4m = 6n \neq 9n$,故A错误;
对于选项B:等式$2m = 3n$左边减3,右边加2,不符合等式性质,故B错误;
对于选项C:等式$2m = 3n$两边同时加3,得$2m + 3 = 3n + 3$,故C正确;
对于选项D:等式$2m = 3n$两边同时除以2,得$m=\frac{3}{2}n \neq \frac{2}{3}n$,故D错误。
C
对于选项B:等式$2m = 3n$左边减3,右边加2,不符合等式性质,故B错误;
对于选项C:等式$2m = 3n$两边同时加3,得$2m + 3 = 3n + 3$,故C正确;
对于选项D:等式$2m = 3n$两边同时除以2,得$m=\frac{3}{2}n \neq \frac{2}{3}n$,故D错误。
C