典例1 如图是一个几何体的表面展开图.
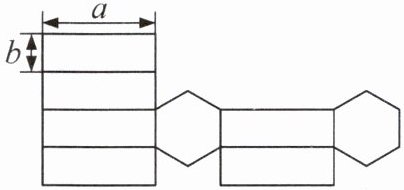
(1)请写出这个几何体的名称;
(2)请根据图中所标的尺寸,直接写出这个几何体的侧面积.(用含a,b的代数式表示)

(1)请写出这个几何体的名称;
(2)请根据图中所标的尺寸,直接写出这个几何体的侧面积.(用含a,b的代数式表示)
答案:【解析】:
(1) 观察几何体的表面展开图,可以看到侧面由6个长方形组成,底面由2个六边形组成。因此,这个几何体是六棱柱。
(2) 六棱柱的侧面积是6个长方形的面积之和。每个长方形的面积为$a × b$,所以6个长方形的面积之和为$6ab$。
【答案】:
(1) 六棱柱。
(2) $6ab$。
(1) 观察几何体的表面展开图,可以看到侧面由6个长方形组成,底面由2个六边形组成。因此,这个几何体是六棱柱。
(2) 六棱柱的侧面积是6个长方形的面积之和。每个长方形的面积为$a × b$,所以6个长方形的面积之和为$6ab$。
【答案】:
(1) 六棱柱。
(2) $6ab$。
【变式1】如图是一个长方体及其表面展开图,阴影部分的面积为$3100cm^2.$
(1)求x的值;
(2)若用一张长方形铁皮直接裁剪,然后做成这个长方体形状的储物盒,则这张铁皮的长和宽至少为多少厘米?

(1)求x的值;
(2)若用一张长方形铁皮直接裁剪,然后做成这个长方体形状的储物盒,则这张铁皮的长和宽至少为多少厘米?

答案:(1)由题意,得20x+20×30+30x=3100,解得x=50.
(2)由题意,得2×(20+30)=100(cm),50+20+20=90(cm).故这张铁皮的长至少为100cm,宽至少为90cm.
(2)由题意,得2×(20+30)=100(cm),50+20+20=90(cm).故这张铁皮的长至少为100cm,宽至少为90cm.
典例2 新素养 空间观念 如图①是由五个边长都是1的正方形纸片拼接而成的,现将图①沿虚线折成一个无盖的正方体纸盒(图②)后,与线段MN重合的线段是(

$A. NB_2$
$B. C_2F$
$C. C_2D_2$
$D. MA_2$
C
)
$A. NB_2$
$B. C_2F$
$C. C_2D_2$
$D. MA_2$
答案:【解析】:本题可根据正方体展开图与折叠后正方体各部分之间的对应关系来求解。
观察正方体的展开图可知,将图①沿虚线折成一个无盖的正方体纸盒后,点$M$与点$D_2$重合,点$N$与点$C_2$重合。
在折叠后的无盖正方体纸盒中,线段$MN$两端点分别与$C_2$、$D_2$重合,所以与线段$MN$重合的线段是$C_2D_2$。
【答案】:C
观察正方体的展开图可知,将图①沿虚线折成一个无盖的正方体纸盒后,点$M$与点$D_2$重合,点$N$与点$C_2$重合。
在折叠后的无盖正方体纸盒中,线段$MN$两端点分别与$C_2$、$D_2$重合,所以与线段$MN$重合的线段是$C_2D_2$。
【答案】:C