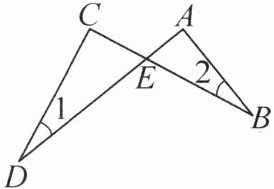
典例3 如图,∠A= ∠C,AD,BC交于点E,∠2= 23°,则∠1的度数为(
A.77°
B.67°
C.45°
D.23°
D
)
A.77°
B.67°
C.45°
D.23°
答案:【解析】:本题可根据平角的定义以及对顶角的性质来求解$\angle1$的度数。
步骤一:根据平角的定义列出等式
因为$\angle C+\angle 1+\angle CED = 180^{\circ}$(平角的定义:平角为$180^{\circ}$),$\angle A+\angle 2+\angle AEB = 180^{\circ}$,所以可得$\angle C+\angle 1+\angle CED=\angle A+\angle 2+\angle AEB$。
步骤二:利用对顶角的性质进行等量代换
由于$\angle CED$与$\angle AEB$是对顶角,根据对顶角的性质:对顶角相等,可知$\angle CED = \angle AEB$。
又已知$\angle A = \angle C$,将$\angle CED = \angle AEB$和$\angle A = \angle C$代入$\angle C+\angle 1+\angle CED=\angle A+\angle 2+\angle AEB$中,可得$\angle 1 = \angle 2$。
步骤三:求出$\angle1$的度数
已知$\angle 2 = 23^{\circ}$,因为$\angle 1 = \angle 2$,所以$\angle 1 = 23^{\circ}$。
【答案】:D
步骤一:根据平角的定义列出等式
因为$\angle C+\angle 1+\angle CED = 180^{\circ}$(平角的定义:平角为$180^{\circ}$),$\angle A+\angle 2+\angle AEB = 180^{\circ}$,所以可得$\angle C+\angle 1+\angle CED=\angle A+\angle 2+\angle AEB$。
步骤二:利用对顶角的性质进行等量代换
由于$\angle CED$与$\angle AEB$是对顶角,根据对顶角的性质:对顶角相等,可知$\angle CED = \angle AEB$。
又已知$\angle A = \angle C$,将$\angle CED = \angle AEB$和$\angle A = \angle C$代入$\angle C+\angle 1+\angle CED=\angle A+\angle 2+\angle AEB$中,可得$\angle 1 = \angle 2$。
步骤三:求出$\angle1$的度数
已知$\angle 2 = 23^{\circ}$,因为$\angle 1 = \angle 2$,所以$\angle 1 = 23^{\circ}$。
【答案】:D
【变式3】如图,直线AB,CD相交于点O。若∠1= 40°,∠3比∠2的2倍多10°,则∠2的度数为(

A.20°
B.25°
C.30°
D.35°
C
)
A.20°
B.25°
C.30°
D.35°
答案:C
解析:
设∠2的度数为$x$,则∠3的度数为$2x + 10^\circ$。
因为直线AB,CD相交于点O,所以∠1与∠2是对顶角的邻补角关系(或∠1+∠2+∠3=180°,根据平角定义),已知∠1=40°,则有:
$40^\circ + x + (2x + 10^\circ) = 180^\circ$
$40^\circ + x + 2x + 10^\circ = 180^\circ$
$3x + 50^\circ = 180^\circ$
$3x = 130^\circ$
$x = 30^\circ$
C
因为直线AB,CD相交于点O,所以∠1与∠2是对顶角的邻补角关系(或∠1+∠2+∠3=180°,根据平角定义),已知∠1=40°,则有:
$40^\circ + x + (2x + 10^\circ) = 180^\circ$
$40^\circ + x + 2x + 10^\circ = 180^\circ$
$3x + 50^\circ = 180^\circ$
$3x = 130^\circ$
$x = 30^\circ$
C
典例4 如图,在四边形ABCD中,AB⊥BC,AC⊥CD,AB= 2,AD= 3,则AC长的取值范围是(

A.AC>2
B.AC<3
C.2<AC<3
D.1<AC<5
C
)
A.AC>2
B.AC<3
C.2<AC<3
D.1<AC<5
答案:【解析】:本题可根据垂线段最短的性质来确定$AC$长的取值范围。
在$\triangle ABC$中,因为$AB\perp BC$,根据垂线段最短可知,在从点$B$到直线$AC$的所有线段中,$AB$是最短的,所以$AB\lt AC$。
已知$AB = 2$,则$AC\gt 2$。
在$\triangle ACD$中,因为$AC\perp CD$,同样根据垂线段最短可知,在从点$C$到直线$AD$的所有线段中,$AC$是最短的,所以$AC\lt AD$。
已知$AD = 3$,则$AC\lt 3$。
综合以上两个结论,可得$2\lt AC\lt 3$。
【答案】:C
在$\triangle ABC$中,因为$AB\perp BC$,根据垂线段最短可知,在从点$B$到直线$AC$的所有线段中,$AB$是最短的,所以$AB\lt AC$。
已知$AB = 2$,则$AC\gt 2$。
在$\triangle ACD$中,因为$AC\perp CD$,同样根据垂线段最短可知,在从点$C$到直线$AD$的所有线段中,$AC$是最短的,所以$AC\lt AD$。
已知$AD = 3$,则$AC\lt 3$。
综合以上两个结论,可得$2\lt AC\lt 3$。
【答案】:C
【变式4】如图,在△ABC中,∠ACB= 90°,AC= 3,BC= 4,AB= 5,P为直线AB上一动点,连接PC,则PC长的最小值是(

A.3
B.2.5
C.2.4
D.2
C
)
A.3
B.2.5
C.2.4
D.2
答案:C
解析:
在△ABC中,∠ACB=90°,AC=3,BC=4,AB=5。当P为直线AB上一动点时,PC长的最小值为点C到直线AB的距离。
根据三角形面积公式,S△ABC=$\frac{1}{2}$×AC×BC=$\frac{1}{2}$×AB×PC。
代入数值:$\frac{1}{2}$×3×4=$\frac{1}{2}$×5×PC,解得PC=$\frac{12}{5}$=2.4。
C
根据三角形面积公式,S△ABC=$\frac{1}{2}$×AC×BC=$\frac{1}{2}$×AB×PC。
代入数值:$\frac{1}{2}$×3×4=$\frac{1}{2}$×5×PC,解得PC=$\frac{12}{5}$=2.4。
C