典例3 新素养 运算能力 已知$|a - 2| + |b - 3| + |c - 4| = 0$,求下面各式的值:
(1)$a + b - c$;
(2)$|a| + |c| - |b|$。
(1)$a + b - c$;
(2)$|a| + |c| - |b|$。
答案:【解析】:本题考察的是绝对值的性质以及基本的代数运算。首先,需要理解绝对值的非负性,即对于任何实数x,有$|x| \geq 0$。然后,根据题目给出的条件$|a - 2| + |b - 3| + |c - 4| = 0$,可以推断出每一项的绝对值都必须为0,因为三个非负数之和为0,那么这三个数都必须为0。由此可以得出$a - 2 = 0$,$b - 3 = 0$,$c - 4 = 0$,从而解出$a = 2$,$b = 3$,$c = 4$。最后,将求得的$a$,$b$,$c$的值代入到两个代数式中计算结果。
【答案】:
(1) 解:由于$|a - 2| = 0$,$|b - 3| = 0$,$|c - 4| = 0$,得出$a = 2$,$b = 3$,$c = 4$。所以,$a + b - c = 2 + 3 - 4 = 1$。
(2) 解:同样地,由于已经得出$a = 2$,$b = 3$,$c = 4$,所以$|a| + |c| - |b| = |2| + |4| - |3| = 2 + 4 - 3 = 3$。
【答案】:
(1) 解:由于$|a - 2| = 0$,$|b - 3| = 0$,$|c - 4| = 0$,得出$a = 2$,$b = 3$,$c = 4$。所以,$a + b - c = 2 + 3 - 4 = 1$。
(2) 解:同样地,由于已经得出$a = 2$,$b = 3$,$c = 4$,所以$|a| + |c| - |b| = |2| + |4| - |3| = 2 + 4 - 3 = 3$。
【变式3】已知$|a| = 3$,$|b| = 2$,且$|a - b| = b - a$,则在数轴上表示a,b两数的点之间的距离为(
A.1或2
B.1或3
C.2或3
D.1或5
D
)A.1或2
B.1或3
C.2或3
D.1或5
答案:D
解析:
因为$|a| = 3$,所以$a = 3$或$a=-3$;因为$|b| = 2$,所以$b = 2$或$b=-2$。
又因为$|a - b| = b - a$,所以$b - a\geq0$,即$b\geq a$。
情况一:当$b = 2$时,$a$需满足$a\leq2$,所以$a=-3$。此时两点距离为$|2 - (-3)| = 5$。
情况二:当$b=-2$时,$a$需满足$a\leq-2$,所以$a=-3$。此时两点距离为$|-2 - (-3)| = 1$。
综上,距离为1或5。D
又因为$|a - b| = b - a$,所以$b - a\geq0$,即$b\geq a$。
情况一:当$b = 2$时,$a$需满足$a\leq2$,所以$a=-3$。此时两点距离为$|2 - (-3)| = 5$。
情况二:当$b=-2$时,$a$需满足$a\leq-2$,所以$a=-3$。此时两点距离为$|-2 - (-3)| = 1$。
综上,距离为1或5。D
典例4 新素养 几何直观 如图,数轴上两点A,B表示的数分别为a,b,则下列各数中最大的是(
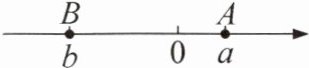
A.$-a + b$
B.$2a$
C.$a + b$
D.$a - b$
D
)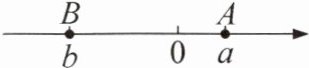
A.$-a + b$
B.$2a$
C.$a + b$
D.$a - b$
答案:【解析】:本题主要考察数轴、绝对值与相反数的相关知识。
首先,根据数轴上的点的位置,我们可以确定$a$和$b$的正负性以及它们绝对值的大小关系。
由图可知,点A在原点右侧,所以$a > 0$;点B在原点左侧,所以$b < 0$。
同时,由于点B到原点的距离大于点A到原点的距离,所以$|b| > |a|$。
接下来,我们逐一分析选项:
A. $-a + b$:由于$a > 0$,$-a < 0$;又因为$b < 0$,所以$-a + b < 0$,即该选项的值为负。
B. $2a$:由于$a > 0$,所以$2a > 0$,即该选项的值为正,但我们需要比较它与其它正选项的大小。
C. $a + b$:由于$a > 0$,$b < 0$,且$|b| > |a|$,所以$a + b < 0$,即该选项的值为负。
D. $a - b$:由于$a > 0$,$b < 0$,所以$a - b > 0$。同时,因为$|b| > |a|$,所以$a - b$的绝对值会大于$2a$(即$|a - b| > |2a|$),在正数中,绝对值大的数本身也大。
综上所述,最大的数是$a - b$。
【答案】:D
首先,根据数轴上的点的位置,我们可以确定$a$和$b$的正负性以及它们绝对值的大小关系。
由图可知,点A在原点右侧,所以$a > 0$;点B在原点左侧,所以$b < 0$。
同时,由于点B到原点的距离大于点A到原点的距离,所以$|b| > |a|$。
接下来,我们逐一分析选项:
A. $-a + b$:由于$a > 0$,$-a < 0$;又因为$b < 0$,所以$-a + b < 0$,即该选项的值为负。
B. $2a$:由于$a > 0$,所以$2a > 0$,即该选项的值为正,但我们需要比较它与其它正选项的大小。
C. $a + b$:由于$a > 0$,$b < 0$,且$|b| > |a|$,所以$a + b < 0$,即该选项的值为负。
D. $a - b$:由于$a > 0$,$b < 0$,所以$a - b > 0$。同时,因为$|b| > |a|$,所以$a - b$的绝对值会大于$2a$(即$|a - b| > |2a|$),在正数中,绝对值大的数本身也大。
综上所述,最大的数是$a - b$。
【答案】:D
【变式4】已知一组数:-3.5,0,$|-5|$,$-(-4)$,$-| - 2|$。
(1) 把这些数在下面的数轴上表示出来:

(2) 请将这些数按从小到大的顺序排列。(用“<”号连接)
(1) 把这些数在下面的数轴上表示出来:

(2) 请将这些数按从小到大的顺序排列。(用“<”号连接)
答案:(1)图略.(2)-3.5<-|-2|<0<-(-4)<|-5|.
解析:
(1)在数轴上表示如下:
在数轴上$-6$和$-5$之间的位置标记$-3.5$;
在原点$0$处标记$0$;
在$5$处标记$|-5|$;
在$4$处标记$-(-4)$;
在$-2$处标记$-|-2|$。
(2)$-3.5 < -|-2| < 0 < -(-4) < |-5|$
在数轴上$-6$和$-5$之间的位置标记$-3.5$;
在原点$0$处标记$0$;
在$5$处标记$|-5|$;
在$4$处标记$-(-4)$;
在$-2$处标记$-|-2|$。
(2)$-3.5 < -|-2| < 0 < -(-4) < |-5|$