例1 粉刷一间教室,甲单独做需要24小时完成,乙单独做需要30小时完成。现在甲、乙两人轮流粉刷。甲粉刷1小时,乙粉刷2小时,甲粉刷1小时,乙粉刷2小时……如此交替下去,粉刷完这间教室需要用多少小时?
我的思考
我的解答
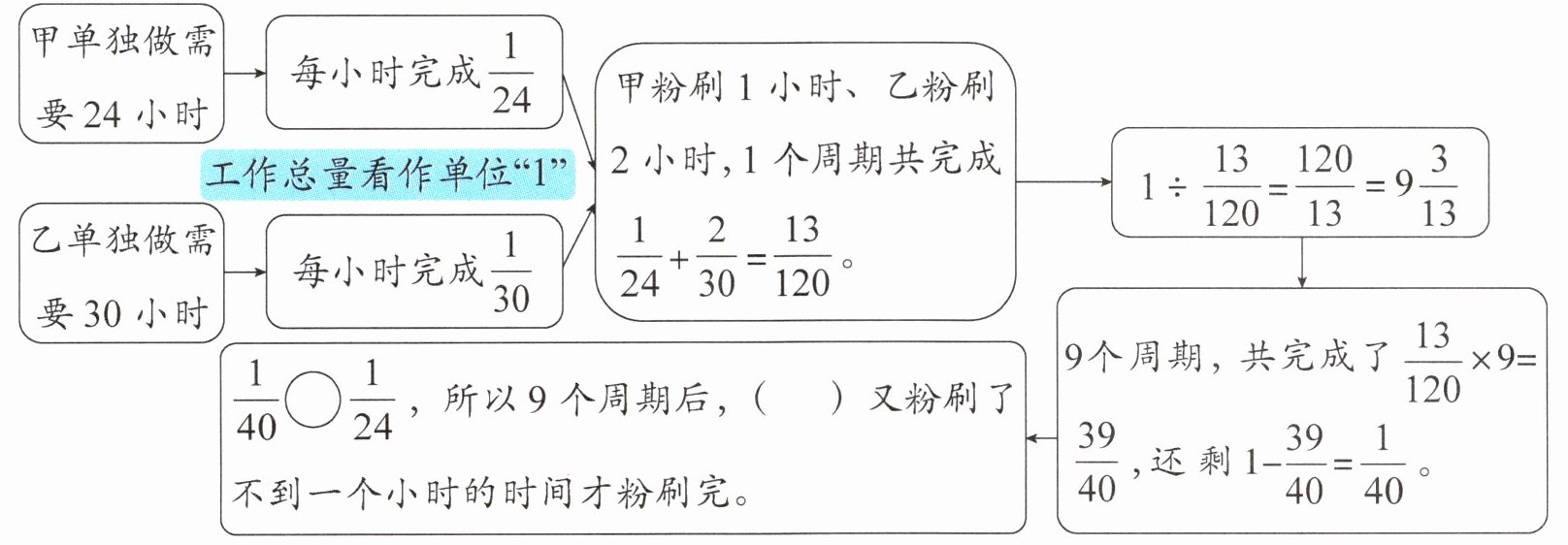
甲粉刷1小时、乙粉刷2小时,1个周期共完成$\frac{1}{24}+\frac{2}{30}= \frac{13}{120},$
$1÷\frac{13}{120}= \frac{120}{13}= 9\frac{3}{13},$所以甲、乙先粉刷9个周期,共完成$\frac{13}{120}×9= \frac{39}{40},$还剩$1-\frac{39}{40}= \frac{1}{40}$未完成。因为$\frac{1}{40}◯\frac{1}{24},$所以甲最后粉刷的时间是( )÷( )= ( )(小时),
所以粉刷这间教室所用的总时间是( )×( )+( )= ( )(小时)。
我的思考

我的解答
甲粉刷1小时、乙粉刷2小时,1个周期共完成$\frac{1}{24}+\frac{2}{30}= \frac{13}{120},$
$1÷\frac{13}{120}= \frac{120}{13}= 9\frac{3}{13},$所以甲、乙先粉刷9个周期,共完成$\frac{13}{120}×9= \frac{39}{40},$还剩$1-\frac{39}{40}= \frac{1}{40}$未完成。因为$\frac{1}{40}◯\frac{1}{24},$所以甲最后粉刷的时间是( )÷( )= ( )(小时),
所以粉刷这间教室所用的总时间是( )×( )+( )= ( )(小时)。
答案:【我的思考】< 甲 【我的解答】< \(\frac{1}{40}\div\frac{1}{24}=\frac{3}{5}\) \(3\times9+\frac{3}{5}=27\frac{3}{5}\)
例2 某工程由甲、乙、丙小队合干,需要5天完成;由乙、丙、丁小队合干,需要4天完成;由甲、丁小队合干,需要12天完成。如果按甲、乙、丙、丁、甲、乙、丙、丁……的顺序,每个小队轮流干一天,那么工程最后由哪个小队完成?一共用时多少天?
我的思考
我的尝试
我的反思
我的思考

我的尝试
我的反思

答案:【我的思考】
$\frac{1}{20}+\frac{1}{12}-\frac{1}{15}=\frac{4}{15}$
$1÷\frac{4}{15}=\frac{15}{4}=3\frac{3}{4}$,$\frac{3}{4}=\frac{1}{5}+\frac{1}{3}$
甲、乙、丙
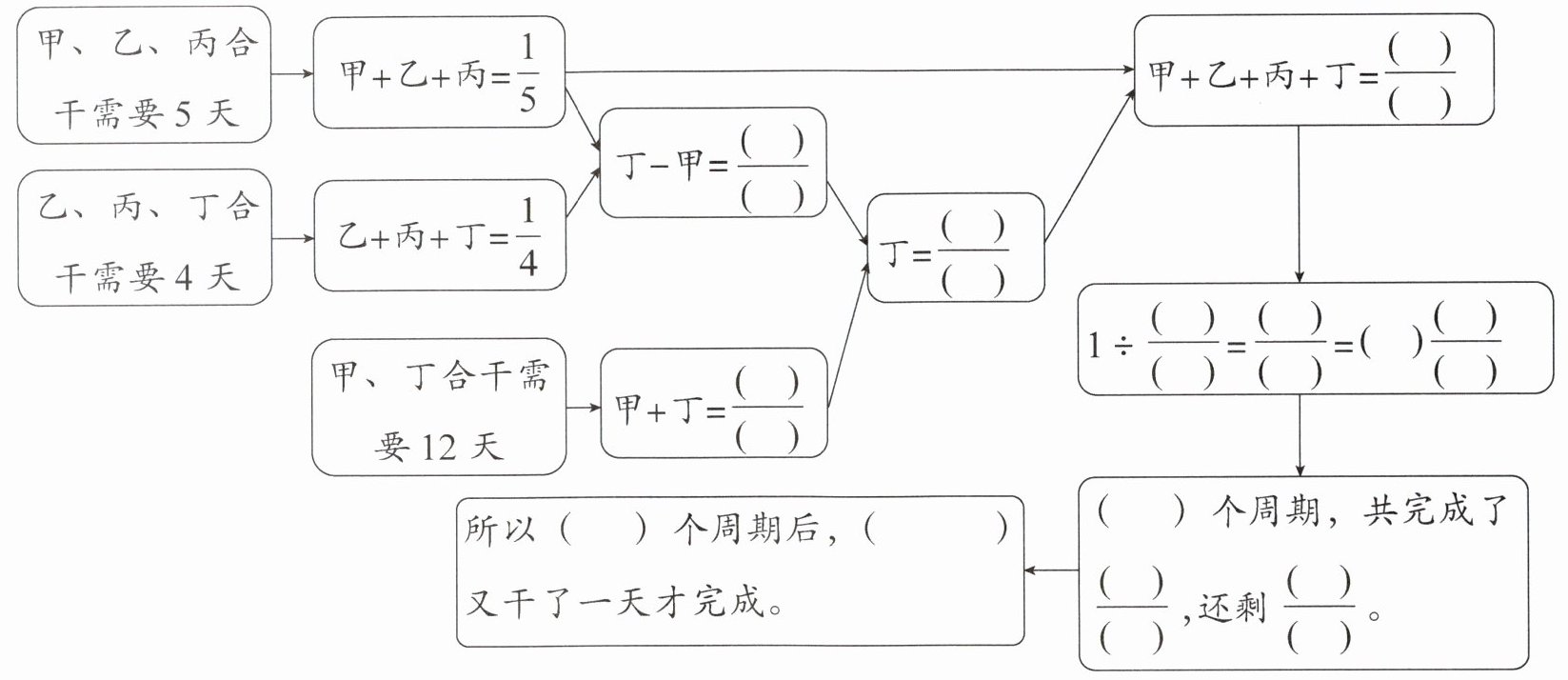
【我的尝试】甲、乙、丙小队的工作效率之和是$\frac{1}{5}$,
乙、丙、丁小队的工作效率之和是$\frac{1}{4}$,
丁小队每天比甲小队多完成这项工程的$\frac{1}{4}-\frac{1}{5}=\frac{1}{20}$,
而甲、丁小队的工作效率之和是$\frac{1}{12}$,
所以丁小队的工作效率是$(\frac{1}{12}+\frac{1}{20})÷2=\frac{1}{15}$,
甲、乙、丙、丁小队的工作效率之和是$\frac{1}{5}+\frac{1}{15}=\frac{4}{15}$,
$1÷\frac{4}{15}=3\frac{3}{4}$,所以$4$个小队轮流干了$3$个完整的周期,$3$个完整的周期完成的工作量是$\frac{4}{15}×3=\frac{4}{5}$,剩余的工作量是$1-\frac{4}{5}=\frac{1}{5}$,
剩余的工作恰好能由甲、乙、丙小队轮流干一天完成,即最后由丙小队完成。
一共用时$4×3 - 1 = 11$(天)。
【我的反思】甲小队的工作效率是$\frac{1}{12}-\frac{1}{15}=\frac{1}{60}$,乙、丙小队的工作效率无法求出,乙、丙小队的工作效率之和是$\frac{1}{5}-\frac{1}{60}=\frac{11}{60}$(或$\frac{1}{4}-\frac{1}{15}=\frac{11}{60}$)。
$\frac{1}{20}+\frac{1}{12}-\frac{1}{15}=\frac{4}{15}$
$1÷\frac{4}{15}=\frac{15}{4}=3\frac{3}{4}$,$\frac{3}{4}=\frac{1}{5}+\frac{1}{3}$
甲、乙、丙
【我的尝试】甲、乙、丙小队的工作效率之和是$\frac{1}{5}$,
乙、丙、丁小队的工作效率之和是$\frac{1}{4}$,
丁小队每天比甲小队多完成这项工程的$\frac{1}{4}-\frac{1}{5}=\frac{1}{20}$,
而甲、丁小队的工作效率之和是$\frac{1}{12}$,
所以丁小队的工作效率是$(\frac{1}{12}+\frac{1}{20})÷2=\frac{1}{15}$,
甲、乙、丙、丁小队的工作效率之和是$\frac{1}{5}+\frac{1}{15}=\frac{4}{15}$,
$1÷\frac{4}{15}=3\frac{3}{4}$,所以$4$个小队轮流干了$3$个完整的周期,$3$个完整的周期完成的工作量是$\frac{4}{15}×3=\frac{4}{5}$,剩余的工作量是$1-\frac{4}{5}=\frac{1}{5}$,
剩余的工作恰好能由甲、乙、丙小队轮流干一天完成,即最后由丙小队完成。
一共用时$4×3 - 1 = 11$(天)。
【我的反思】甲小队的工作效率是$\frac{1}{12}-\frac{1}{15}=\frac{1}{60}$,乙、丙小队的工作效率无法求出,乙、丙小队的工作效率之和是$\frac{1}{5}-\frac{1}{60}=\frac{11}{60}$(或$\frac{1}{4}-\frac{1}{15}=\frac{11}{60}$)。