3. 新定义考法
如图①,在$\angle AOB内部画射线OC$,得到三个角,分别为$\angle AOC$、$\angle BOC$、$\angle AOB$。若这三个角中有两个角的度数比是$2:1$,则称射线$OC是\angle AOB$的一条“幸运线”。(本题中所研究的角都小于$180^{\circ}$)
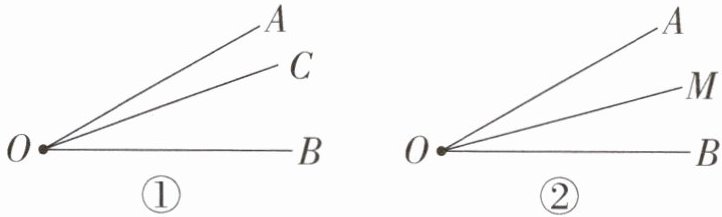
|阅读理解| |
|(1)|如图②,$\angle AOM = \angle MOB$,射线$OM$(
|初步应用| |
|(2)|已知$\angle AOB = 48^{\circ}$,射线$ON是\angle AOB$的“幸运线”,那么$\angle AON = $(
|解决问题| |
|(3)|如图③,已知$\angle COD = 50^{\circ}$,射线$OP从OC$出发,以每秒$10^{\circ}的速度绕点O$按顺时针方向旋转;同时,射线$OQ从OD$出发,以每秒$15^{\circ}的速度绕点O$按顺时针方向旋转。设旋转的时间为$t$秒($0 < t < 5$),若某一时刻$OP$、$OQ$、$OD$三条射线中,一条射线恰好是另外两条射线组成的角的“幸运线”,求$t$的值。|

如图①,在$\angle AOB内部画射线OC$,得到三个角,分别为$\angle AOC$、$\angle BOC$、$\angle AOB$。若这三个角中有两个角的度数比是$2:1$,则称射线$OC是\angle AOB$的一条“幸运线”。(本题中所研究的角都小于$180^{\circ}$)
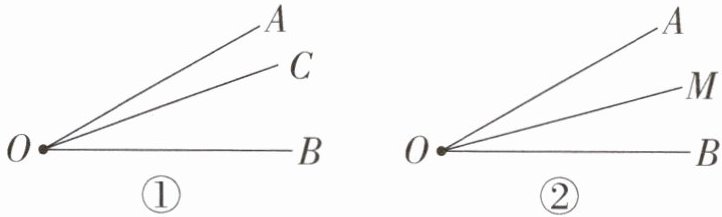
|阅读理解| |
|(1)|如图②,$\angle AOM = \angle MOB$,射线$OM$(
是
)$\angle AOB$的“幸运线”。(填“是”或“不是”)||初步应用| |
|(2)|已知$\angle AOB = 48^{\circ}$,射线$ON是\angle AOB$的“幸运线”,那么$\angle AON = $(
16°或24°或32°
)。||解决问题| |
|(3)|如图③,已知$\angle COD = 50^{\circ}$,射线$OP从OC$出发,以每秒$10^{\circ}的速度绕点O$按顺时针方向旋转;同时,射线$OQ从OD$出发,以每秒$15^{\circ}的速度绕点O$按顺时针方向旋转。设旋转的时间为$t$秒($0 < t < 5$),若某一时刻$OP$、$OQ$、$OD$三条射线中,一条射线恰好是另外两条射线组成的角的“幸运线”,求$t$的值。|

当∠POQ = 2∠DOQ时,15t = 1/2(50 + 5t),t = 2;当∠DOP = 2∠DOQ时,50 - 10t = 2×15t,t = 5/4;当∠DOQ = 2∠DOP时,15t = 2(50 - 10t),t = 20/7。综上,t的值是2或5/4或20/7。
答案:
(1)是 提示:根据题意,∠AOB = 2∠AOM,所以∠AOB与∠AOM的度数比是2:1,射线OM是∠AOB的“幸运线”。
(2)16°或24°或32° 提示:当∠NOB = 2∠AON时,∠AON = 48°÷(2 + 1) = 16°;当∠AOB = 2∠AON时,∠AON = 48°÷2 = 24°;当∠AON = 2∠NOB时,∠AON = 48°÷(2 + 1)×2 = 32°。
(3)当∠POQ = 2∠DOQ时,15t = 1/2(50 + 5t),t = 2;当∠DOP = 2∠DOQ时,50 - 10t = 2×15t,t = 5/4;当∠DOQ = 2∠DOP时,15t = 2(50 - 10t),t = 20/7。综上,t的值是2或5/4或20/7。 提示:当0<t<5时,射线OP在∠COD内部,此时∠POQ = 15t + 50 - 10t = (50 + 5t)°,∠DOQ = 15t°。当∠POQ = 2∠DOQ时,则∠DOQ = 1/2∠POQ,即15t = 1/2(50 + 5t),解得t = 2;当∠DOP = 2∠DOQ时,则50 - 10t = 2×15t,解得t = 5/4;当∠DOQ = 2∠DOP时,则15t = 2(50 - 10t),解得t = 20/7。综上,t的值是2或5/4或20/7。
(1)是 提示:根据题意,∠AOB = 2∠AOM,所以∠AOB与∠AOM的度数比是2:1,射线OM是∠AOB的“幸运线”。
(2)16°或24°或32° 提示:当∠NOB = 2∠AON时,∠AON = 48°÷(2 + 1) = 16°;当∠AOB = 2∠AON时,∠AON = 48°÷2 = 24°;当∠AON = 2∠NOB时,∠AON = 48°÷(2 + 1)×2 = 32°。
(3)当∠POQ = 2∠DOQ时,15t = 1/2(50 + 5t),t = 2;当∠DOP = 2∠DOQ时,50 - 10t = 2×15t,t = 5/4;当∠DOQ = 2∠DOP时,15t = 2(50 - 10t),t = 20/7。综上,t的值是2或5/4或20/7。 提示:当0<t<5时,射线OP在∠COD内部,此时∠POQ = 15t + 50 - 10t = (50 + 5t)°,∠DOQ = 15t°。当∠POQ = 2∠DOQ时,则∠DOQ = 1/2∠POQ,即15t = 1/2(50 + 5t),解得t = 2;当∠DOP = 2∠DOQ时,则50 - 10t = 2×15t,解得t = 5/4;当∠DOQ = 2∠DOP时,则15t = 2(50 - 10t),解得t = 20/7。综上,t的值是2或5/4或20/7。
4. 探究题
某不规则容器如图所示,两名同学就“这个不规则容器的容积是多少?”的问题进行了探究。(忽略容器壁厚)

(1)朵朵想:把不规则容器分成上、下两部分,上半部分如图中的涂色部分,上半部分的容积为(

(2)乐乐想:若在不规则容器的上方放置一个完全一样的容器,可以拼成一个大长方体容器,如图,请按乐乐的想法解答。

50×30×(8 + 20)÷2 = 21000(立方厘米)
21000立方厘米 = 21立方分米
某不规则容器如图所示,两名同学就“这个不规则容器的容积是多少?”的问题进行了探究。(忽略容器壁厚)

(1)朵朵想:把不规则容器分成上、下两部分,上半部分如图中的涂色部分,上半部分的容积为(
9
)立方分米,这个不规则容器的容积为(21
)立方分米。
(2)乐乐想:若在不规则容器的上方放置一个完全一样的容器,可以拼成一个大长方体容器,如图,请按乐乐的想法解答。

50×30×(8 + 20)÷2 = 21000(立方厘米)
21000立方厘米 = 21立方分米
答案:
(1)9 21 提示:上半部分的容积为50×30×(20 - 8)÷2 = 9000(立方厘米),9000立方厘米 = 9立方分米,下半部分的容积为50×30×8 = 12000(立方厘米),12000立方厘米 = 12立方分米,这个不规则容器的容积为9 + 12 = 21(立方分米)。
(2)50×30×(8 + 20)÷2 = 21000(立方厘米)21000立方厘米 = 21立方分米 提示:两个不规则的容器拼成一个大长方体后,长是50厘米,宽是30厘米,高是(20 + 8)厘米,求出这个大长方体的容积,再除以2,就是这个不规则容器的容积。
(1)9 21 提示:上半部分的容积为50×30×(20 - 8)÷2 = 9000(立方厘米),9000立方厘米 = 9立方分米,下半部分的容积为50×30×8 = 12000(立方厘米),12000立方厘米 = 12立方分米,这个不规则容器的容积为9 + 12 = 21(立方分米)。
(2)50×30×(8 + 20)÷2 = 21000(立方厘米)21000立方厘米 = 21立方分米 提示:两个不规则的容器拼成一个大长方体后,长是50厘米,宽是30厘米,高是(20 + 8)厘米,求出这个大长方体的容积,再除以2,就是这个不规则容器的容积。