5. 数形结合
我国著名数学家华罗庚曾说过:“数缺形时少直观,形少数时难入微。”在数学中,数与形之间可以相互转化。乐乐利用数形结合的方法来验证$a^{2}-b^{2}= (a + b)×(a - b)$。
在边长为$a的正方形纸片上剪去一个边长为b$($b < a$)的小正方形,剩余部分的面积可以用两种方法来求出,如图。
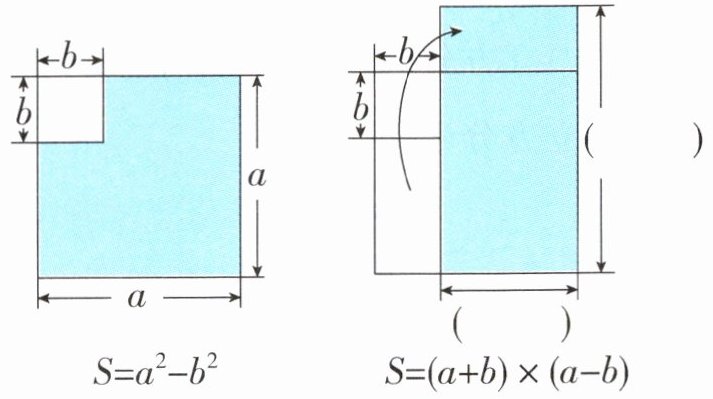
(1)请你帮他将图中的标注补全。
(2)请你应用上面的方法来计算。
$(1-\frac{1}{2}×\frac{1}{2})×(1-\frac{1}{3}×\frac{1}{3})×(1-\frac{1}{4}×\frac{1}{4})×…×(1-\frac{1}{2026}×\frac{1}{2026})$。
我国著名数学家华罗庚曾说过:“数缺形时少直观,形少数时难入微。”在数学中,数与形之间可以相互转化。乐乐利用数形结合的方法来验证$a^{2}-b^{2}= (a + b)×(a - b)$。
在边长为$a的正方形纸片上剪去一个边长为b$($b < a$)的小正方形,剩余部分的面积可以用两种方法来求出,如图。

(1)请你帮他将图中的标注补全。
a + b
a - b
(2)请你应用上面的方法来计算。
$(1-\frac{1}{2}×\frac{1}{2})×(1-\frac{1}{3}×\frac{1}{3})×(1-\frac{1}{4}×\frac{1}{4})×…×(1-\frac{1}{2026}×\frac{1}{2026})$。
$(1 - 1/2×1/2)×(1 - 1/3×1/3)×(1 - 1/4×1/4)×…×(1 - 1/2026×1/2026)=(1 + 1/2)×(1 - 1/2)×(1 + 1/3)×(1 - 1/3)×(1 + 1/4)×(1 - 1/4)×…×(1 + 1/2026)×(1 - 1/2026)=3/2×1/2×4/3×2/3×5/4×3/4×…×2027/2026×2025/2026=1/2×2027/2026=2027/4052$
答案:
(1)a + b a - b 提示:大正方形的边长是a,剪去的部分是边长为b的小正方形,那么拼成的大长方形的长是(a + b),宽是(a - b)。
(2)(1 - 1/2×1/2)×(1 - 1/3×1/3)×(1 - 1/4×1/4)×…×(1 - 1/2026×1/2026)=(1 + 1/2)×(1 - 1/2)×(1 + 1/3)×(1 - 1/3)×(1 + 1/4)×(1 - 1/4)×…×(1 + 1/2026)×(1 - 1/2026)=3/2×1/2×4/3×2/3×5/4×3/4×…×2027/2026×2025/2026=1/2×2027/2026=2027/4052
提示:1 - 1/2×1/2 = 1²-(1/2)²,1 - 1/3×1/3 = 1²-(1/3)²……由上面的方法,可知a² - b²=(a + b)×(a - b),将算式转化为(a + b)×(a - b),化简后即可算出得数。
(1)a + b a - b 提示:大正方形的边长是a,剪去的部分是边长为b的小正方形,那么拼成的大长方形的长是(a + b),宽是(a - b)。
(2)(1 - 1/2×1/2)×(1 - 1/3×1/3)×(1 - 1/4×1/4)×…×(1 - 1/2026×1/2026)=(1 + 1/2)×(1 - 1/2)×(1 + 1/3)×(1 - 1/3)×(1 + 1/4)×(1 - 1/4)×…×(1 + 1/2026)×(1 - 1/2026)=3/2×1/2×4/3×2/3×5/4×3/4×…×2027/2026×2025/2026=1/2×2027/2026=2027/4052
提示:1 - 1/2×1/2 = 1²-(1/2)²,1 - 1/3×1/3 = 1²-(1/3)²……由上面的方法,可知a² - b²=(a + b)×(a - b),将算式转化为(a + b)×(a - b),化简后即可算出得数。
6. 分类讨论
如图,点$D是等腰直角三角形ABC的底边AB$的中点,点$P在线段AB$上移动,点$Q是线段AP$的中点。某一时刻$PD = \frac{3}{2}$分米,$PQ = \frac{5}{2}$分米。

(1)此时线段$BP$的长度是多少分米?
(2)三角形$ABC$的面积是多少平方分米?
如图,点$D是等腰直角三角形ABC的底边AB$的中点,点$P在线段AB$上移动,点$Q是线段AP$的中点。某一时刻$PD = \frac{3}{2}$分米,$PQ = \frac{5}{2}$分米。

(1)此时线段$BP$的长度是多少分米?
(2)三角形$ABC$的面积是多少平方分米?
答案:
(1)(5/2+5/2+3/2)×2 - 5/2×2 = 8(分米)或(5/2+5/2 - 3/2)×2 - 5/2×2 = 2(分米) 提示:当点P在点D的左侧时,BP = (5/2+5/2+3/2)×2 - 5/2×2 = 8(分米)。当点P在点D的右侧时,BP = (5/2+5/2 - 3/2)×2 - 5/2×2 = 2(分米)。
(2)①AD=5/2×2 + 3/2=13/2(分米)13/2×13/2=169/4(平方分米)②AD=5/2×2 - 3/2=7/2(分米)7/2×7/2=49/4(平方分米)所以三角形ABC的面积是169/4平方分米或49/4平方分米。 提示:连接CD,因为三角形ABC为等腰直角三角形,点D是底边AB的中点,所以AB = 2AD = 2CD,且CD垂直于AB,所以AD = CD,S三角形ABC=AB×CD÷2 = 2AD×CD÷2 = AD×CD = AD×AD。当点P在点D的左侧时,AD=5/2 + 5/2 + 3/2=13/2(分米),则S三角形ABC=13/2×13/2=169/4(平方分米);当点P在点D的右侧时,AD=5/2 + 5/2 - 3/2=7/2(分米),则S三角形ABC=7/2×7/2=49/4(平方分米)。综上,三角形ABC的面积为169/4平方分米或49/4平方分米。
(1)(5/2+5/2+3/2)×2 - 5/2×2 = 8(分米)或(5/2+5/2 - 3/2)×2 - 5/2×2 = 2(分米) 提示:当点P在点D的左侧时,BP = (5/2+5/2+3/2)×2 - 5/2×2 = 8(分米)。当点P在点D的右侧时,BP = (5/2+5/2 - 3/2)×2 - 5/2×2 = 2(分米)。
(2)①AD=5/2×2 + 3/2=13/2(分米)13/2×13/2=169/4(平方分米)②AD=5/2×2 - 3/2=7/2(分米)7/2×7/2=49/4(平方分米)所以三角形ABC的面积是169/4平方分米或49/4平方分米。 提示:连接CD,因为三角形ABC为等腰直角三角形,点D是底边AB的中点,所以AB = 2AD = 2CD,且CD垂直于AB,所以AD = CD,S三角形ABC=AB×CD÷2 = 2AD×CD÷2 = AD×CD = AD×AD。当点P在点D的左侧时,AD=5/2 + 5/2 + 3/2=13/2(分米),则S三角形ABC=13/2×13/2=169/4(平方分米);当点P在点D的右侧时,AD=5/2 + 5/2 - 3/2=7/2(分米),则S三角形ABC=7/2×7/2=49/4(平方分米)。综上,三角形ABC的面积为169/4平方分米或49/4平方分米。
7. 极限思想
如果$A = 1÷(\frac{1}{90}+\frac{1}{91}+\frac{1}{92}+…+\frac{1}{98}+\frac{1}{99})$,那么$A$的整数部分是多少?
如果$A = 1÷(\frac{1}{90}+\frac{1}{91}+\frac{1}{92}+…+\frac{1}{98}+\frac{1}{99})$,那么$A$的整数部分是多少?
答案:因为1/90>1/91>1/92>…>1/99,所以1/90+1/91+1/92+…+1/98+1/99<1/90×10=1/9,1/90+1/91+1/92+…+1/98+1/99>1/99×10=10/99。所以9<A<99/10,即9<A<9.9,所以A的整数部分是9。
解析:
因为$\frac{1}{90}>\frac{1}{91}>\frac{1}{92}>\dots>\frac{1}{99}$,所以$\frac{1}{90}+\frac{1}{91}+\frac{1}{92}+\dots+\frac{1}{98}+\frac{1}{99}<\frac{1}{90}×10=\frac{1}{9}$,$\frac{1}{90}+\frac{1}{91}+\frac{1}{92}+\dots+\frac{1}{98}+\frac{1}{99}>\frac{1}{99}×10=\frac{10}{99}$。因此$9 < A < \frac{99}{10}$,即$9 < A < 9.9$,故$A$的整数部分是$9$。
8. 代换思想
乐乐将1440毫升的水装入甲、乙两个壶中,若先装满甲壶,剩余的水可装乙壶的$\frac{1}{2}$,若先装满乙壶,剩余的水可装甲壶的$\frac{4}{5}$,则这两个壶分别可以装多少毫升的水?
乐乐将1440毫升的水装入甲、乙两个壶中,若先装满甲壶,剩余的水可装乙壶的$\frac{1}{2}$,若先装满乙壶,剩余的水可装甲壶的$\frac{4}{5}$,则这两个壶分别可以装多少毫升的水?
答案:甲壶:1440÷6×5 = 1200(毫升) 乙壶:1200÷5×2 = 480(毫升)
提示:因为甲壶 + 乙壶 = 甲壶+1/2乙壶+1/2乙壶 = 乙壶+4/5甲壶+1/5甲壶,由题知甲壶+1/2乙壶 = 乙壶+4/5甲壶= 1440毫升,所以1/2乙壶=1/5甲壶,把1440毫升平均分成6份,那么甲壶占其中的5份,即甲壶= 1440÷6×5 = 1200(毫升),乙壶= 1200÷5×2 = 480(毫升)。
提示:因为甲壶 + 乙壶 = 甲壶+1/2乙壶+1/2乙壶 = 乙壶+4/5甲壶+1/5甲壶,由题知甲壶+1/2乙壶 = 乙壶+4/5甲壶= 1440毫升,所以1/2乙壶=1/5甲壶,把1440毫升平均分成6份,那么甲壶占其中的5份,即甲壶= 1440÷6×5 = 1200(毫升),乙壶= 1200÷5×2 = 480(毫升)。