5. (1)丢沙包是一款多人玩的经典游戏。手工课上,乐乐用碎布缝合了 6 块正方形布,准备做正方体沙包。他用五谷杂粮填充后的成品是哪一个?圈一圈。
(2)空间观念 一个正方体的小木块,1 与 6、2 与 5、3 与 4 分别是相对面。如图那样放置,并按图中箭头指示的方向翻动,则木块翻动到第 5 格时,木块正上方那一面的数字是( )。
(3)一个棱长为 10 厘米的正方体水箱内已注入一些水,若将它沿着某条棱旋转,使得正方体两个面与地面的夹角都是 45°,如图为此水箱的侧面视图,此时水面标记在 A、D 两点,如果需要添加 125 立方厘米的水,才能将此水箱注满,那么三角形 ACD 的面积是( )平方厘米。
(4)如图①,将一个棱长为 10 的正方体从顶点 A 切掉一个棱长为 4 的正方体,得到如图②所示的立体图形。这个立体图形的表面积是( );如果再从顶点 B 切掉一个棱长为 6 的正方体,那么剩下的立体图形的表面积是( )。

(5)推理意识 一个长方体,前面和上面的面积之和是 209 平方厘米,这个长方体的长、宽、高都是以厘米为单位的质数,这个长方体的体积是( )立方厘米。
(2)空间观念 一个正方体的小木块,1 与 6、2 与 5、3 与 4 分别是相对面。如图那样放置,并按图中箭头指示的方向翻动,则木块翻动到第 5 格时,木块正上方那一面的数字是( )。
(3)一个棱长为 10 厘米的正方体水箱内已注入一些水,若将它沿着某条棱旋转,使得正方体两个面与地面的夹角都是 45°,如图为此水箱的侧面视图,此时水面标记在 A、D 两点,如果需要添加 125 立方厘米的水,才能将此水箱注满,那么三角形 ACD 的面积是( )平方厘米。
(4)如图①,将一个棱长为 10 的正方体从顶点 A 切掉一个棱长为 4 的正方体,得到如图②所示的立体图形。这个立体图形的表面积是( );如果再从顶点 B 切掉一个棱长为 6 的正方体,那么剩下的立体图形的表面积是( )。

(5)推理意识 一个长方体,前面和上面的面积之和是 209 平方厘米,这个长方体的长、宽、高都是以厘米为单位的质数,这个长方体的体积是( )立方厘米。
答案:
(1) 提示:根据展开图和立体图形的前面图案想象从上面和右面看到的图案是什么,可知成品是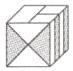
(2)3 提示:可以通过空间位置关系去想象,也可以实际动手做一做,可以发现,从第1格翻动到第5格时,正上方依次出现的数字为6、5、4、6、3,所以最后木块正上方那一面的数字是3。
(3)12.5 提示:水箱是正方体,将BCEF面移到上方,如图。由题可知,需要添加125立方厘米的水才能将水箱加满,即底面是三角形、高是10厘米的这个柱体的体积是125立方厘米,由三棱柱的体积=底面积×高,可得三角形ACD的面积是125÷10=12.5(平方厘米)。
(4)600 568 提示:第一次从A点切掉一个正方体,表面积和原来的正方体相同,为10×10×6=600。从顶点B切掉的情形,我们分析一下从A、B切掉的这两个角,大正方体棱长为10,因此从A点切去的棱长为4的正方体和从B点切去的棱长为6的正方体是有重叠的,这样一来,表面不仅仅只是“凹”进去那么简单了,而是有一部分消失了,如图所示,阴影部分就是那部分消失的面积,阴影部分正好是两个边长为4的正方形,所以再从顶点B切掉棱长为6的正方体后,表面积比原来少了4×4×2=32,所以总表面积为600 - 32=568。
(5)374 提示:根据前面和上面的面积之和是209平方厘米可得长×(高+宽)=209(平方厘米),长、宽、高都是以厘米为单位的质数,将209分解质因数,可得209=19×11,那么宽+高=11或宽+高=19,因为11=2+9=3+8=4+7=5+6,不管怎么组合都有合数,而19=2+17=3+16=4+15=5+14=6+13=7+12=8+11=9+10,其中只有2+17的组合都是质数,所以宽、高分别为2厘米、17厘米。根据公式得体积为11×17×2=374(立方厘米)。
(1) 提示:根据展开图和立体图形的前面图案想象从上面和右面看到的图案是什么,可知成品是

(2)3 提示:可以通过空间位置关系去想象,也可以实际动手做一做,可以发现,从第1格翻动到第5格时,正上方依次出现的数字为6、5、4、6、3,所以最后木块正上方那一面的数字是3。
(3)12.5 提示:水箱是正方体,将BCEF面移到上方,如图。由题可知,需要添加125立方厘米的水才能将水箱加满,即底面是三角形、高是10厘米的这个柱体的体积是125立方厘米,由三棱柱的体积=底面积×高,可得三角形ACD的面积是125÷10=12.5(平方厘米)。

(4)600 568 提示:第一次从A点切掉一个正方体,表面积和原来的正方体相同,为10×10×6=600。从顶点B切掉的情形,我们分析一下从A、B切掉的这两个角,大正方体棱长为10,因此从A点切去的棱长为4的正方体和从B点切去的棱长为6的正方体是有重叠的,这样一来,表面不仅仅只是“凹”进去那么简单了,而是有一部分消失了,如图所示,阴影部分就是那部分消失的面积,阴影部分正好是两个边长为4的正方形,所以再从顶点B切掉棱长为6的正方体后,表面积比原来少了4×4×2=32,所以总表面积为600 - 32=568。

(5)374 提示:根据前面和上面的面积之和是209平方厘米可得长×(高+宽)=209(平方厘米),长、宽、高都是以厘米为单位的质数,将209分解质因数,可得209=19×11,那么宽+高=11或宽+高=19,因为11=2+9=3+8=4+7=5+6,不管怎么组合都有合数,而19=2+17=3+16=4+15=5+14=6+13=7+12=8+11=9+10,其中只有2+17的组合都是质数,所以宽、高分别为2厘米、17厘米。根据公式得体积为11×17×2=374(立方厘米)。
6. 有大、中、小三个正方体水池,它们的内部棱长分别是 6 米、3 米、2 米。三个水池都装了半池水。现将两堆碎石分别沉没在中、小水池的水里,两个水池的水面分别升高了 6 厘米和 4 厘米。如果将两堆碎石都沉没在大水池的水里,大水池的水面会升高多少厘米?(结果精确到小数点后两位)
答案:3米=300厘米 2米=200厘米 6米=600厘米 300×300×6=540000(立方厘米) 200×200×4=160000(立方厘米) (160000+540000)÷(600×600)=$\frac{35}{18}$≈1.94(厘米) 提示:先求水池中的碎石体积:中水池底面正方形边长为3米,水面升高6厘米,这堆碎石的体积=300×300×6=540000(立方厘米)。再求小水池中的碎石体积:小水池底面正方形边长为2米,水面升高4厘米,这堆碎石的体积=200×200×4=160000(立方厘米)。所以两堆碎石的体积一共为160000+540000=700000(立方厘米)。把它们放入大水池,水池中水面升高部分的体积就是700000立方厘米。由于大水池底面正方形边长为6米,所以大水池的水面上升的高度为700000÷(600×600)=$\frac{35}{18}$≈1.94(厘米)。
解析:
3米=300厘米,2米=200厘米,6米=600厘米。
中水池碎石体积:$300×300×6 = 540000$(立方厘米)。
小水池碎石体积:$200×200×4 = 160000$(立方厘米)。
两堆碎石总体积:$540000 + 160000 = 700000$(立方厘米)。
大水池水面升高高度:$\frac{700000}{600×600} = \frac{35}{18} \approx 1.94$(厘米)。
答:大水池的水面会升高约$1.94$厘米。
中水池碎石体积:$300×300×6 = 540000$(立方厘米)。
小水池碎石体积:$200×200×4 = 160000$(立方厘米)。
两堆碎石总体积:$540000 + 160000 = 700000$(立方厘米)。
大水池水面升高高度:$\frac{700000}{600×600} = \frac{35}{18} \approx 1.94$(厘米)。
答:大水池的水面会升高约$1.94$厘米。
7. 一个长方体容器,底面是一个边长为 60 厘米的正方形。容器里直立着一个高 1 米的长方体铁块,长方体铁块的底面是边长为 15 厘米的正方形。这时容器里的水深 50 厘米,如图①。现在把铁块轻轻地向上提起 24 厘米,如图②,那么露出水面的铁块上被水浸湿部分的面积为多少平方厘米?


答案:
15×15×24÷(60×60 - 15×15)+24=25.6(厘米) 25.6×15×4=1536(平方厘米) 提示:这道题目要求铁块上被水浸湿部分的面积,其实就是求浸湿的长度。当铁块提起来的时候,水面会下降,那么水面下降的部分相当于填充了铁块提起来之后所留下的那段空白,如图所示,我们画出了一个分解图:先提起铁块,露出一片空白,然后水才会进入,这样水面下降的高度就可以算出了。我们可以看到,水面下降部分相当于填充了铁块提起来之后所留下的那段空白,而铁块浸湿的部分则由两部分构成,一部分是原来的24厘米,一部分是由于水面下降所露出来的部分,因此我们只需要求出水面下降了多少,就可以求出铁块浸湿的长度了。根据水的体积不变这个基本条件,铁块提起后留下的空白部分体积为15×15×24=5400(立方厘米),水面本来是一个底面积为60×60 - 15×15=3375(平方厘米)的柱体,因此水面下降的高度就是5400÷3375=1.6(厘米),也就是说,当铁块提起来24厘米之后,有25.6厘米的部分是浸湿的,很容易求得面积为25.6×15×4=1536(平方厘米)。
15×15×24÷(60×60 - 15×15)+24=25.6(厘米) 25.6×15×4=1536(平方厘米) 提示:这道题目要求铁块上被水浸湿部分的面积,其实就是求浸湿的长度。当铁块提起来的时候,水面会下降,那么水面下降的部分相当于填充了铁块提起来之后所留下的那段空白,如图所示,我们画出了一个分解图:先提起铁块,露出一片空白,然后水才会进入,这样水面下降的高度就可以算出了。我们可以看到,水面下降部分相当于填充了铁块提起来之后所留下的那段空白,而铁块浸湿的部分则由两部分构成,一部分是原来的24厘米,一部分是由于水面下降所露出来的部分,因此我们只需要求出水面下降了多少,就可以求出铁块浸湿的长度了。根据水的体积不变这个基本条件,铁块提起后留下的空白部分体积为15×15×24=5400(立方厘米),水面本来是一个底面积为60×60 - 15×15=3375(平方厘米)的柱体,因此水面下降的高度就是5400÷3375=1.6(厘米),也就是说,当铁块提起来24厘米之后,有25.6厘米的部分是浸湿的,很容易求得面积为25.6×15×4=1536(平方厘米)。
