例1 如图,有一个长方体,中间挖去一个正方体,求剩下物体的表面积。(单位:厘米)
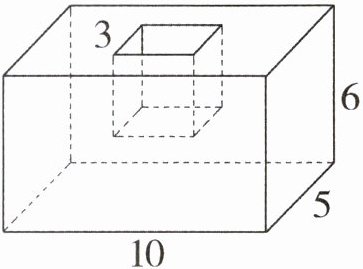
分析:从图中可以看出剩下物体的表面积比原来增加了,正方体的底面向上平移到与长方体上面平齐,所求剩下物体的表面积就是原长方体的表面积与挖去的正方体的前、后、左、右四个面的面积和。
解答:$(10×5+10×6+5×6)×2+3×3×4= 316$(平方厘米)

分析:从图中可以看出剩下物体的表面积比原来增加了,正方体的底面向上平移到与长方体上面平齐,所求剩下物体的表面积就是原长方体的表面积与挖去的正方体的前、后、左、右四个面的面积和。
解答:$(10×5+10×6+5×6)×2+3×3×4= 316$(平方厘米)
答案:分析:
本题考查长方体、正方体表面积的计算。
从图中可以看出剩下物体的表面积比原来增加了,正方体的底面向上平移到与长方体上面平齐,所求剩下物体的表面积就是原长方体的表面积与挖去的正方体的前、后、左、右四个面的面积和。
长方体的表面积为:$2×(长×宽+长×高+宽×高)$,
正方体的四个侧面面积为:$4×棱长×棱长$。
解答:
$(10×5 + 10×6 + 5×6)×2 + 3×3×4$
$= (50 + 60 + 30)×2 + 36$
$= 140×2 + 36$
$= 280 + 36$
$= 316(平方厘米)$
所以,剩下物体的表面积是$316$平方厘米。
本题考查长方体、正方体表面积的计算。
从图中可以看出剩下物体的表面积比原来增加了,正方体的底面向上平移到与长方体上面平齐,所求剩下物体的表面积就是原长方体的表面积与挖去的正方体的前、后、左、右四个面的面积和。
长方体的表面积为:$2×(长×宽+长×高+宽×高)$,
正方体的四个侧面面积为:$4×棱长×棱长$。
解答:
$(10×5 + 10×6 + 5×6)×2 + 3×3×4$
$= (50 + 60 + 30)×2 + 36$
$= 140×2 + 36$
$= 280 + 36$
$= 316(平方厘米)$
所以,剩下物体的表面积是$316$平方厘米。
1. 从一个棱长为8厘米的正方体木料上,割去一个长8厘米,宽和高都是3厘米的小长方体木料,有如图三种方法,剩余部分的表面积按从大到小排列是(
③②①
)。(填序号)答案:③②① 提示:利用平移可发现,切割前后,题图①表面积和之前相比,少了两个边长为3厘米的小正方形的面积,所以剩余部分的表面积为8×8×6 - 3×3×2 = 366(平方厘米);题图②表面积和之前相比,少了两个边长为3厘米的小正方形的面积,多了两个长8厘米、宽3厘米的小长方形的面积,所以剩余部分的表面积为8×8×6 + 3×8×2 - 3×3×2 = 414(平方厘米);题图③表面积和之前相比,少了两个边长为3厘米的小正方形的面积,多了四个长8厘米、宽3厘米的小长方形的面积,所以剩余部分的表面积为8×8×6 + 3×8×4 - 3×3×2 = 462(平方厘米)。因为366 < 414 < 462,所以③ > ② > ①,故填③②①。
2. 在一个长、宽、高分别是8厘米、5厘米、4厘米的长方体的8个顶点处,分别截下一个棱长为1厘米的小正方体后,剩下物体的表面积是(
184
)平方厘米。答案:184 提示:剩下物体的表面积与原来长方体的表面积相同,是(8×5 + 8×4 + 5×4)×2 = 184(平方厘米)。
解析:
原来长方体表面积为$(8×5 + 8×4 + 5×4)×2$
$=(40 + 32 + 20)×2$
$=92×2$
$=184$(平方厘米)
在顶点处截下小正方体,每个顶点处减少3个小正方形面,同时增加3个小正方形面,表面积不变,故剩下物体表面积是184平方厘米。
184
$=(40 + 32 + 20)×2$
$=92×2$
$=184$(平方厘米)
在顶点处截下小正方体,每个顶点处减少3个小正方形面,同时增加3个小正方形面,表面积不变,故剩下物体表面积是184平方厘米。
184
3. 如图,在一个棱长为5分米的正方体上面的正中间向下挖一个棱长为2分米的正方体小洞,接着在小洞的底面正中间再向下挖一个棱长为1分米的正方体小洞。挖洞后的立体图形的表面积是多少平方分米?


答案:5×5×6 + 2×2×4 + 1×1×4 = 170(平方分米) 提示:将挖洞后棱长为1分米的正方体的底面与棱长为2分米的正方体的底面都向上平移至棱长为5分米的正方体的上面,这样挖洞后的立体图形的表面积 = 棱长为5分米的正方体表面积 + 棱长为2分米的正方体的四个侧面面积之和 + 棱长为1分米的正方体的四个侧面面积之和。
解析:
$5×5×6 + 2×2×4 + 1×1×4$
$=25×6 + 4×4 + 1×4$
$=150 + 16 + 4$
$=170$(平方分米)
答:挖洞后的立体图形的表面积是170平方分米。
$=25×6 + 4×4 + 1×4$
$=150 + 16 + 4$
$=170$(平方分米)
答:挖洞后的立体图形的表面积是170平方分米。
例2 一根高3米的长方体钢材,其底面是正方形。截去75厘米长的一段后,剩下的钢材的表面积比原来减少1.2平方米,求原来钢材的体积。

分析:如图,截去75厘米长的一段后,它的表面积和原来相比,只减少了高是75厘米的一段长方体钢材的侧面的面积。根据减少的表面积和这根钢材的底面是正方形,可求出这根钢材的底面边长,再利用公式求出原长方体钢材的体积。
解答:75厘米= 0.75米 $1.2÷0.75= 1.6$(米)
$1.6÷4= 0.4$(米) $0.4×0.4×3= 0.48$(立方米)

分析:如图,截去75厘米长的一段后,它的表面积和原来相比,只减少了高是75厘米的一段长方体钢材的侧面的面积。根据减少的表面积和这根钢材的底面是正方形,可求出这根钢材的底面边长,再利用公式求出原长方体钢材的体积。
解答:75厘米= 0.75米 $1.2÷0.75= 1.6$(米)
$1.6÷4= 0.4$(米) $0.4×0.4×3= 0.48$(立方米)
答案:本题可先将单位统一,再根据减少的表面积求出底面周长,进而求出底面边长,最后根据长方体体积公式求出原来钢材的体积。
步骤一:单位换算
因为$1$米$ = 100$厘米,所以$75$厘米换算为米是:$75÷100 = 0.75$米。
步骤二:求底面周长
截去$75$厘米长的一段后,表面积减少的部分就是高为$0.75$米的长方体的侧面积。
根据长方体侧面积公式$S = Ch$(其中$S$为侧面积,$C$为底面周长,$h$为高),已知侧面积$S = 1.2$平方米,高$h = 0.75$米,可得底面周长$C$为:
$1.2÷0.75 = 1.6$(米)
步骤三:求底面边长
因为该长方体钢材底面是正方形,正方形的周长公式为$C = 4a$(其中$C$为周长,$a$为边长),已知底面周长$C = 1.6$米,所以底面边长$a$为:
$1.6÷4 = 0.4$(米)
步骤四:求原来钢材的体积
根据长方体体积公式$V = Sh$(其中$V$为体积,$S$为底面积,$h$为高),已知底面边长$a = 0.4$米,则底面积$S = 0.4×0.4 = 0.16$平方米,原来钢材的高$h = 3$米,所以原来钢材的体积$V$为:
$0.4×0.4×3 = 0.48$(立方米)
综上,原来钢材的体积是$0.48$立方米。
步骤一:单位换算
因为$1$米$ = 100$厘米,所以$75$厘米换算为米是:$75÷100 = 0.75$米。
步骤二:求底面周长
截去$75$厘米长的一段后,表面积减少的部分就是高为$0.75$米的长方体的侧面积。
根据长方体侧面积公式$S = Ch$(其中$S$为侧面积,$C$为底面周长,$h$为高),已知侧面积$S = 1.2$平方米,高$h = 0.75$米,可得底面周长$C$为:
$1.2÷0.75 = 1.6$(米)
步骤三:求底面边长
因为该长方体钢材底面是正方形,正方形的周长公式为$C = 4a$(其中$C$为周长,$a$为边长),已知底面周长$C = 1.6$米,所以底面边长$a$为:
$1.6÷4 = 0.4$(米)
步骤四:求原来钢材的体积
根据长方体体积公式$V = Sh$(其中$V$为体积,$S$为底面积,$h$为高),已知底面边长$a = 0.4$米,则底面积$S = 0.4×0.4 = 0.16$平方米,原来钢材的高$h = 3$米,所以原来钢材的体积$V$为:
$0.4×0.4×3 = 0.48$(立方米)
综上,原来钢材的体积是$0.48$立方米。
4. (1)一个正方体,如果高增加3厘米,它的表面积就增加60平方厘米,原来这个正方体的体积是( )立方厘米。
(2)一个长方体,从下部和上部分别截去高为3厘米和2厘米的长方体后,便成为一个正方体,其表面积减少了120平方厘米,原长方体的体积是( )立方厘米。
(2)一个长方体,从下部和上部分别截去高为3厘米和2厘米的长方体后,便成为一个正方体,其表面积减少了120平方厘米,原长方体的体积是( )立方厘米。
答案:
(1)125 提示:高增加3厘米,表面积就增加60平方厘米,则正方体的底面周长是60÷3 = 20(厘米),正方体的棱长是20÷4 = 5(厘米),体积是5×5×5 = 125(立方厘米)。
(2)396 提示:如图,表面积减少了120平方厘米,指高度分别为2厘米和3厘米的两个长方体前、后、左、右四个面的面积之和,那么正方体的底面周长是120÷(2 + 3) = 24(厘米),正方体的棱长就是24÷4 = 6(厘米)。这样原长方体的体积就可以求出了。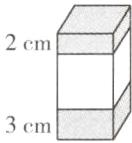
(1)125 提示:高增加3厘米,表面积就增加60平方厘米,则正方体的底面周长是60÷3 = 20(厘米),正方体的棱长是20÷4 = 5(厘米),体积是5×5×5 = 125(立方厘米)。
(2)396 提示:如图,表面积减少了120平方厘米,指高度分别为2厘米和3厘米的两个长方体前、后、左、右四个面的面积之和,那么正方体的底面周长是120÷(2 + 3) = 24(厘米),正方体的棱长就是24÷4 = 6(厘米)。这样原长方体的体积就可以求出了。
