5. 如图,将若干个相同的小正方体叠成一个长方体,这个长方体的底面就是原正方体的底面。如果整个长方体的表面积是2664平方厘米,当从这个长方体的顶部拿去一个正方体后,新长方体的表面积比原来减少144平方厘米。原来有多少个小正方体?
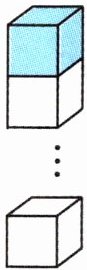

答案:144÷4 = 36(平方厘米) (2664 - 36×2)÷144 = 18(个) 提示:拿去顶部一个小正方体后表面积减少4个面,共144平方厘米,那么小正方体一个面的面积是36平方厘米。整个长方体表面积减去上、下两个面面积后是2664 - 36×2 = 2592(平方厘米),所以原来有2592÷144 = 18(个)小正方体。
解析:
144÷4=36(平方厘米)
(2664-36×2)÷144=18(个)
答:原来有18个小正方体。
(2664-36×2)÷144=18(个)
答:原来有18个小正方体。
例3 如图,把4个完全一样的正方体拼成一个长方体,这个长方体的表面积是540平方厘米,原来一个正方体的表面积是多少平方厘米?

分析:拼成长方体后,有6个面重合,长方体的表面积是在4个小正方体表面积之和的基础上,减少了6个小正方形的面积。所以长方体的表面积就是$24-6= 18$(个)小正方形面积的和。解决此类问题,要注意增加或减少的是哪些面。
解答:$6×4-2×(4-1)= 18$(个)
$540÷18×6= 180$(平方厘米)

分析:拼成长方体后,有6个面重合,长方体的表面积是在4个小正方体表面积之和的基础上,减少了6个小正方形的面积。所以长方体的表面积就是$24-6= 18$(个)小正方形面积的和。解决此类问题,要注意增加或减少的是哪些面。
解答:$6×4-2×(4-1)= 18$(个)
$540÷18×6= 180$(平方厘米)
答案:解析:本题考查通过长方体表面积求正方体表面积,关键在于找出长方体表面积与正方体一个面面积的关系,进而求出正方体表面积。
设正方体一个面的面积为$x$平方厘米。
4个完全一样的正方体拼成长方体后,表面积减少了$6$个正方形的面积,此时长方体的表面积相当于$18$个正方形的面积。
已知长方体表面积是$540$平方厘米,可据此列出$18x = 540$,求解$x$,再根据正方体表面积公式求出一个正方体的表面积。
答案:
解:设原来正方体一个面的面积为$x$平方厘米。
$18x = 540$
$x = 540÷18$
$x = 30$
则原来一个正方体的表面积是$6×30 = 180$(平方厘米)。
答:原来一个正方体的表面积是$180$平方厘米。
设正方体一个面的面积为$x$平方厘米。
4个完全一样的正方体拼成长方体后,表面积减少了$6$个正方形的面积,此时长方体的表面积相当于$18$个正方形的面积。
已知长方体表面积是$540$平方厘米,可据此列出$18x = 540$,求解$x$,再根据正方体表面积公式求出一个正方体的表面积。
答案:
解:设原来正方体一个面的面积为$x$平方厘米。
$18x = 540$
$x = 540÷18$
$x = 30$
则原来一个正方体的表面积是$6×30 = 180$(平方厘米)。
答:原来一个正方体的表面积是$180$平方厘米。
6. 把5个完全一样的正方体拼成一个长方体后,棱长总和减少了160厘米,原来正方体的棱长是(
5
)厘米,拼成后的长方体棱长总和是(140
)厘米。答案:5 140 提示:拼成的长方体有8个面重合,每个面少了4条棱,共少了8×4 = 32(条)棱,则棱长 = 160÷32 = 5(厘米),棱长总和为4×2×5 + 4×5×5 = 140(厘米)。
解析:
5个正方体拼成长方体,重合面有$ (5-1)×2 = 8 $个,每个重合面减少$ 4 $条棱,共减少棱:$ 8×4 = 32 $(条)。
正方体棱长:$ 160÷32 = 5 $(厘米)。
长方体长:$ 5×5 = 25 $厘米,宽和高均为$ 5 $厘米。
长方体棱长总和:$ 4×(25 + 5 + 5) = 4×35 = 140 $(厘米)。
5;140
正方体棱长:$ 160÷32 = 5 $(厘米)。
长方体长:$ 5×5 = 25 $厘米,宽和高均为$ 5 $厘米。
长方体棱长总和:$ 4×(25 + 5 + 5) = 4×35 = 140 $(厘米)。
5;140
7. 有一个长方体木块,长是10厘米,宽是8厘米,高是6厘米,把它切割成棱长是2厘米的小正方体,这些小正方体的表面积之和比原来长方体的表面积增加了多少平方厘米?
答案:(10÷2)×(8÷2)×(6÷2) = 60(个) 2×2×6×60 - (10×8 + 10×6 + 8×6)×2 = 1064(平方厘米) 提示:先求出切割成的小正方体的个数,再用这些小正方体的表面积之和减去原来长方体的表面积便可求出增加的表面积。
解析:
小正方体的个数:$(10÷2)×(8÷2)×(6÷2)=5×4×3 = 60$(个)
小正方体的表面积之和:$2×2×6×60=1440$(平方厘米)
原来长方体的表面积:$(10×8 + 10×6 + 8×6)×2=(80 + 60 + 48)×2=188×2 = 376$(平方厘米)
增加的表面积:$1440-376 = 1064$(平方厘米)
答:这些小正方体的表面积之和比原来长方体的表面积增加了1064平方厘米。
小正方体的表面积之和:$2×2×6×60=1440$(平方厘米)
原来长方体的表面积:$(10×8 + 10×6 + 8×6)×2=(80 + 60 + 48)×2=188×2 = 376$(平方厘米)
增加的表面积:$1440-376 = 1064$(平方厘米)
答:这些小正方体的表面积之和比原来长方体的表面积增加了1064平方厘米。
例4 有一个长方体储水箱,如果把一个底面是边长为5厘米的正方形的长方体铁块全部放入水中,水面就上升9厘米(水没有溢出);如果把长方体铁块竖直拉出水面8厘米后,水面就下降4厘米。这个长方体铁块的体积是多少立方厘米?
分析:根据“把长方体铁块竖直拉出水面8厘米后,水面就下降4厘米”可知,当水面下降1厘米时,长方体铁块被竖直拉出水面$8÷4= 2$(厘米)。由题意得如果把长方体铁块从水中全部竖直拉出水面,水面就会下降9厘米,则铁块的高度为$2×9= 18$(厘米)。这个长方体铁块的体积是$5×5×18= 450$(立方厘米)。
解答:$5×5×(8÷4×9)= 450$(立方厘米)
分析:根据“把长方体铁块竖直拉出水面8厘米后,水面就下降4厘米”可知,当水面下降1厘米时,长方体铁块被竖直拉出水面$8÷4= 2$(厘米)。由题意得如果把长方体铁块从水中全部竖直拉出水面,水面就会下降9厘米,则铁块的高度为$2×9= 18$(厘米)。这个长方体铁块的体积是$5×5×18= 450$(立方厘米)。
解答:$5×5×(8÷4×9)= 450$(立方厘米)
答案:解析:
本题主要考查长方体体积的计算。
首先,需要理解题目中的关键信息:
当铁块完全放入水中,水面上升了9厘米。
当铁块被竖直拉出水面8厘米,水面下降了4厘米。
根据这两个信息,可以推断出:
当水面下降1厘米时,铁块被拉出的高度是 8/4 = 2(厘米)。
所以,当铁块完全被拉出(即水面下降9厘米)时,铁块的高度是 2×9 = 18(厘米)。
已知铁块的底面是一个边长为5厘米的正方形,所以铁块的体积 V 可以通过以下公式计算:
V = 底面积 × 高 = 5×5 × 18 = 450(立方厘米)。
答案:
这个长方体铁块的体积是 450 立方厘米。
本题主要考查长方体体积的计算。
首先,需要理解题目中的关键信息:
当铁块完全放入水中,水面上升了9厘米。
当铁块被竖直拉出水面8厘米,水面下降了4厘米。
根据这两个信息,可以推断出:
当水面下降1厘米时,铁块被拉出的高度是 8/4 = 2(厘米)。
所以,当铁块完全被拉出(即水面下降9厘米)时,铁块的高度是 2×9 = 18(厘米)。
已知铁块的底面是一个边长为5厘米的正方形,所以铁块的体积 V 可以通过以下公式计算:
V = 底面积 × 高 = 5×5 × 18 = 450(立方厘米)。
答案:
这个长方体铁块的体积是 450 立方厘米。
8. 一个长方体容器的底面是一个边长为60厘米的正方形,容器里直立着一个高1米,底面是边长为18厘米的正方形的长方体铁块,这时容器里的水深0.5米。如果把铁块取出,容器里水深是多少厘米?
答案:0.5米 = 50厘米 50 - 18×18×50÷(60×60) = 45.5(厘米) 提示:根据题意可知,有0.5米高的铁块浸没在水中,用浸没在水中的铁块的体积除以容器的底面积,便可求出水面下降的高度。然后用0.5米减去下降的高度,就是铁块取出后容器里的水面高度。
解析:
0.5米=50厘米
$18×18×50=16200$(立方厘米)
$60×60=3600$(平方厘米)
$16200÷3600=4.5$(厘米)
$50 - 4.5=45.5$(厘米)
答:容器里水深是45.5厘米。
$18×18×50=16200$(立方厘米)
$60×60=3600$(平方厘米)
$16200÷3600=4.5$(厘米)
$50 - 4.5=45.5$(厘米)
答:容器里水深是45.5厘米。
9. 一个长方体水箱,从里面量长40厘米,宽30厘米,深35厘米,箱中水面高10厘米,放入一个棱长是20厘米的正方体铁块后,铁块顶面仍高于水面。这时水面的高度是多少厘米?
答案:40×30×10÷(40×30 - 20×20) = 15(厘米) 提示:正方体铁块放入水中后,水箱内的水与底面接触的面积是(40×30 - 20×20)平方厘米,用水箱内水的体积除以水与底面接触的面积,便是现在的水面高度。
解析:
水箱内水的体积为:$40×30×10 = 12000$(立方厘米)
放入铁块后,水与底面接触的面积为:$40×30 - 20×20 = 1200 - 400 = 800$(平方厘米)
这时水面的高度是:$12000÷800 = 15$(厘米)
答:这时水面的高度是15厘米。
放入铁块后,水与底面接触的面积为:$40×30 - 20×20 = 1200 - 400 = 800$(平方厘米)
这时水面的高度是:$12000÷800 = 15$(厘米)
答:这时水面的高度是15厘米。