1. 在括号里填上合适的单位。
明明从容积是 625 (
明明从容积是 625 (
升
) 的冰箱里, 拿出一盒 250 (毫升
) 的牛奶加热喝完, 吃了两片体积大约是 0.4 (立方分米
) 的吐司面包, 背着体积大约是 45 (立方分米
) 的背包出门, 路上看到一辆厢式货车的体积约是 55 (立方米
)。答案:升 毫升 立方分米 立方分米 立方米
2. $ 5900 \mathrm{dm}^{3}= $
$ 8.8 \mathrm{L}= $
$ 6.03 \mathrm{m}^{3}= $
5.9
$\mathrm{m}^{3} $$ 8.8 \mathrm{L}= $
8.8
$\mathrm{dm}^{3}=$8800
$\mathrm{cm}^{3} $$ 6.03 \mathrm{m}^{3}= $
6
$\mathrm{m}^{3}$30
$\mathrm{dm}^{3} $答案:5.9 8.8 8800 6 30
解析:
5.9;8.8;8800;6;30
3. 一个长方体的底面是边长 5 厘米的正方形, 高是 6 厘米, 它的棱长总和是 (
64
) 厘米, 表面积是 (170
) 平方厘米, 体积是 (150
) 立方厘米。答案:64 170 150
解析:
棱长总和:$(5+5+6)×4=64$厘米
表面积:$5×5×2+5×6×4=170$平方厘米
体积:$5×5×6=150$立方厘米
64 170 150
表面积:$5×5×2+5×6×4=170$平方厘米
体积:$5×5×6=150$立方厘米
64 170 150
4. 把 100 升水倒入棱长为 5 分米的正方体鱼缸内, 水面距鱼缸口还有 (
1
) 分米。(鱼缸玻璃厚度忽略不计)答案:1
解析:
5×5=25(平方分米)
100升=100立方分米
100÷25=4(分米)
5-4=1(分米)
1
100升=100立方分米
100÷25=4(分米)
5-4=1(分米)
1
5. 在一个长 40 厘米、宽 20 厘米、高 25 厘米、水深 18 厘米的长方体水槽内浸没一个小球, 将小球取出后, 水深 17.2 厘米。这个小球的体积是 (
640
) 立方厘米, 水槽内水与水槽的接触面积减少 (96
) 平方厘米。答案:640 96
解析:
小球体积:$40×20×(18 - 17.2)=40×20×0.8 = 640$(立方厘米)
接触面积减少:$2×(40 + 20)×(18 - 17.2)=2×60×0.8 = 96$(平方厘米)
640 96
接触面积减少:$2×(40 + 20)×(18 - 17.2)=2×60×0.8 = 96$(平方厘米)
640 96
6. 用一张长 8 厘米、宽 6 厘米的长方形纸围成一个底面是正方形的长方体的侧面, 这个长方体的底面积可能是 (
4
) 平方厘米, 也可能是 (2.25
) 平方厘米。答案:4 2.25
解析:
情况一:以长方形的长为底面正方形的周长
底面正方形边长:$8÷4 = 2$(厘米)
底面积:$2×2 = 4$(平方厘米)
情况二:以长方形的宽为底面正方形的周长
底面正方形边长:$6÷4 = 1.5$(厘米)
底面积:$1.5×1.5 = 2.25$(平方厘米)
4 2.25
底面正方形边长:$8÷4 = 2$(厘米)
底面积:$2×2 = 4$(平方厘米)
情况二:以长方形的宽为底面正方形的周长
底面正方形边长:$6÷4 = 1.5$(厘米)
底面积:$1.5×1.5 = 2.25$(平方厘米)
4 2.25
7. 用三个长 3 厘米、宽 2 厘米、高 1 厘米的长方体拼成一个大长方体, 这个大长方体的棱长之和最大是 (
48
) 厘米, 表面积最大是 (58
) 平方厘米, 最小是 (42
) 平方厘米。答案:48 58 42
解析:
要使大长方体棱长之和最大,应将最小面(2×1)拼接,此时大长方体长为$3×3 = 9$厘米,宽2厘米,高1厘米。棱长之和为$4×(9 + 2 + 1)=4×12 = 48$厘米。
要使表面积最大,拼接最小面(2×1),减少$4$个$2×1$的面。每个小长方体表面积为$2×(3×2 + 3×1 + 2×1)=2×11 = 22$平方厘米,三个小长方体表面积之和为$3×22 = 66$平方厘米,大长方体表面积为$66 - 4×(2×1)=66 - 8 = 58$平方厘米。
要使表面积最小,拼接最大面(3×2),减少$4$个$3×2$的面。大长方体表面积为$66 - 4×(3×2)=66 - 24 = 42$平方厘米。
48 58 42
要使表面积最大,拼接最小面(2×1),减少$4$个$2×1$的面。每个小长方体表面积为$2×(3×2 + 3×1 + 2×1)=2×11 = 22$平方厘米,三个小长方体表面积之和为$3×22 = 66$平方厘米,大长方体表面积为$66 - 4×(2×1)=66 - 8 = 58$平方厘米。
要使表面积最小,拼接最大面(3×2),减少$4$个$3×2$的面。大长方体表面积为$66 - 4×(3×2)=66 - 24 = 42$平方厘米。
48 58 42
8. 林叔叔靠一面墙用篱笆围了一个长 8 分米、宽 6 分米、高 4 分米的长方体形状的鸡圈 (墙足够长), 这个鸡圈至少需要篱笆 (
80
) 平方分米。答案:80
9. 把一个长 100 厘米、宽 60 厘米、高 45 厘米的长方体木块切割成棱长是 15 厘米的正方体, 最多能切 (
72
) 个, 切完后剩下的边角料的体积是 (27000
) 立方厘米。答案:72 27000
解析:
100÷15=6(个)……10(厘米)
60÷15=4(个)
45÷15=3(个)
6×4×3=72(个)
100×60×45=270000(立方厘米)
15×15×15×72=243000(立方厘米)
270000-243000=27000(立方厘米)
72 27000
60÷15=4(个)
45÷15=3(个)
6×4×3=72(个)
100×60×45=270000(立方厘米)
15×15×15×72=243000(立方厘米)
270000-243000=27000(立方厘米)
72 27000
10. 一个长方体的长是 5 分米, 宽是 2 分米, 高是 3 分米。如果要使这个长方体的表面积增加 20 平方分米, 宽和高都不变, 长应增加 (
2
) 分米。答案:2
解析:
设长应增加$x$分米。
增加的表面积为$2×(2x + 3x)=20$
$2×5x=20$
$10x=20$
$x=2$
2
增加的表面积为$2×(2x + 3x)=20$
$2×5x=20$
$10x=20$
$x=2$
2
11. 如图, 小华在一个无盖的长方体玻璃容器中摆了若干个体积为 1 立方厘米的小正方体。这个玻璃容器的表面积是 (
96
) 平方厘米。由小正方体拼成的立体图形的表面积是 (50
) 平方厘米, 容器内最多还能再放 (78
) 个这样的小正方体。答案:96 50 78
12. 如图, 把一个正方体分成两个一样的长方体, 其中一个长方体的表面积是 48 平方厘米, 正方体的表面积是 (
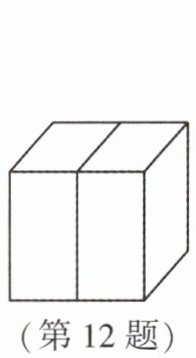
72
) 平方厘米。
答案:72
解析:
设正方体的棱长为$a$厘米。
正方体表面积为$6a^2$平方厘米。
分成两个一样的长方体后,每个长方体的长、宽、高分别为$a$厘米、$a$厘米、$\frac{a}{2}$厘米。
长方体表面积为$2(a× a + a×\frac{a}{2} + a×\frac{a}{2}) = 2(a^2 + \frac{a^2}{2} + \frac{a^2}{2}) = 2(2a^2) = 4a^2$平方厘米。
已知长方体表面积为48平方厘米,即$4a^2 = 48$,解得$a^2 = 12$。
正方体表面积为$6a^2 = 6×12 = 72$平方厘米。
72
正方体表面积为$6a^2$平方厘米。
分成两个一样的长方体后,每个长方体的长、宽、高分别为$a$厘米、$a$厘米、$\frac{a}{2}$厘米。
长方体表面积为$2(a× a + a×\frac{a}{2} + a×\frac{a}{2}) = 2(a^2 + \frac{a^2}{2} + \frac{a^2}{2}) = 2(2a^2) = 4a^2$平方厘米。
已知长方体表面积为48平方厘米,即$4a^2 = 48$,解得$a^2 = 12$。
正方体表面积为$6a^2 = 6×12 = 72$平方厘米。
72
13. 把一个表面涂满红色的大正方体切成棱长为 1 厘米的小正方体。
(1) 如果 2 面涂色的小正方体有 36 个, 那么原来大正方体的体积是 ( ) 立方厘米。
(2) 如果 1 面涂色的小正方体有 96 个, 那么没有涂色的小正方体有 ( ) 个。
(1) 如果 2 面涂色的小正方体有 36 个, 那么原来大正方体的体积是 ( ) 立方厘米。
(2) 如果 1 面涂色的小正方体有 96 个, 那么没有涂色的小正方体有 ( ) 个。
答案:
(1)125 提示:如图,2面涂色的有36个,那么n=5,即原来大正方体的棱长是5厘米,体积是5×5×5=125(立方厘米)。

(2)64 提示:如图,1面涂色的有96个,那么n=6,即原来大正方体的棱长是6厘米,那么没有涂色的小正方体有$(6 - 2)^3$ = 64(个)。
(1)125 提示:如图,2面涂色的有36个,那么n=5,即原来大正方体的棱长是5厘米,体积是5×5×5=125(立方厘米)。

(2)64 提示:如图,1面涂色的有96个,那么n=6,即原来大正方体的棱长是6厘米,那么没有涂色的小正方体有$(6 - 2)^3$ = 64(个)。
14. 一个装满牛奶的长方体牛奶盒, 长 6 厘米, 宽 5 厘米, 高 12 厘米。乐乐倒出一些牛奶后, 盒中空出的部分如图所示, 乐乐倒出了 (

90
) 毫升牛奶。
答案:90 提示:由题意可知,乐乐倒出的牛奶的体积就是长6厘米,宽5厘米,高6厘米的长方体的体积的一半。
解析:
由题意可知,乐乐倒出的牛奶的体积为长6厘米、宽5厘米、高6厘米的长方体体积的一半。
长方体体积公式:$V = 长×宽×高$
则该长方体体积为:$6×5×6 = 180$(立方厘米)
倒出牛奶体积为:$180×\frac{1}{2} = 90$(立方厘米)
因为1立方厘米=1毫升,所以90立方厘米=90毫升。
90
长方体体积公式:$V = 长×宽×高$
则该长方体体积为:$6×5×6 = 180$(立方厘米)
倒出牛奶体积为:$180×\frac{1}{2} = 90$(立方厘米)
因为1立方厘米=1毫升,所以90立方厘米=90毫升。
90