6.
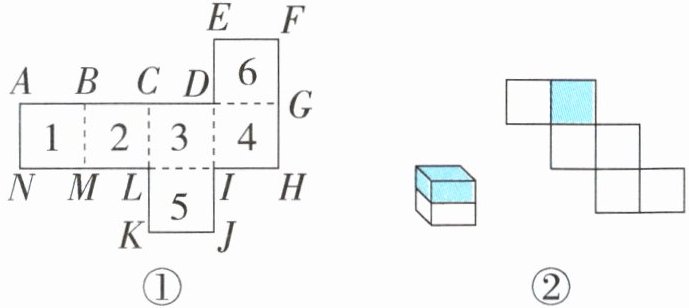
(1)将图①沿棱折成一个正方体,相交于一个顶点的三个面上的数字之和最大是( )。
(2)图①折叠成一个正方体后,和点N重合的是点( )和( )。
(3)图②的正方体上半部分被涂上了颜色,请把它的展开图中的涂色部分补充完整。

(1)将图①沿棱折成一个正方体,相交于一个顶点的三个面上的数字之和最大是( )。
(2)图①折叠成一个正方体后,和点N重合的是点( )和( )。
(3)图②的正方体上半部分被涂上了颜色,请把它的展开图中的涂色部分补充完整。
答案:
(1)13 提示:最大的两个数“5”和“6”在对面,不可能有公共顶点,所以最大只能是3+4+6=13。
(2)H J 提示:折起来后,1、4、5三个面共一个顶点N,则和点N重合的是点H和J。
(3)补充完整如图:
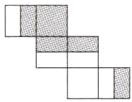
提示:与题中展开图中全部涂色的面相对的面不涂色,根据折起来的位置,把与全部涂色的面相邻的4个面的上半部分涂色即可。
(1)13 提示:最大的两个数“5”和“6”在对面,不可能有公共顶点,所以最大只能是3+4+6=13。
(2)H J 提示:折起来后,1、4、5三个面共一个顶点N,则和点N重合的是点H和J。
(3)补充完整如图:

提示:与题中展开图中全部涂色的面相对的面不涂色,根据折起来的位置,把与全部涂色的面相邻的4个面的上半部分涂色即可。
7. (1)快递公司把客户要寄送的物品用一个长方体的纸箱包装好,再用包装带按如图所示的方法捆起来(接头处共长20厘米),一共要用包装带( )厘米。

(2)一个长方体的左右侧面是正方形,相交于同一顶点的三条棱中两条棱的长度分别是6厘米和4厘米,这个长方体的棱长和可能是( )厘米,也可能是( )厘米。
(3)林轩在一张长方形纸上画了一个棱长为4厘米的正方体的展开图,则这张长方形纸的面积至少是( )平方厘米。
(4)一个正方体,6个面上分别写了6个连续的整数,且每组相对面上的两个数之和都相等,下图中能看到的数为16、19和20,则这6个整数的和是( )。


(2)一个长方体的左右侧面是正方形,相交于同一顶点的三条棱中两条棱的长度分别是6厘米和4厘米,这个长方体的棱长和可能是( )厘米,也可能是( )厘米。
(3)林轩在一张长方形纸上画了一个棱长为4厘米的正方体的展开图,则这张长方形纸的面积至少是( )平方厘米。
(4)一个正方体,6个面上分别写了6个连续的整数,且每组相对面上的两个数之和都相等,下图中能看到的数为16、19和20,则这6个整数的和是( )。

答案:
(1)620 提示:包装带的总长度=4条长+4条宽+8条高+接头处的包装带长。50×4+40×4+30×8+20=620(厘米)。
(2)64 56 提示:长方体的左右侧面是正方形,且相交于同一顶点的三条棱中两条棱的长度分别是6厘米和4厘米,那么另一条棱长是6厘米或4厘米,则棱长和是6×8+4×4=64(厘米)或4×8+6×4=56(厘米)。
(3)160 提示:当正方体的展开图如图所示时,长方形纸的面积最小,是(4×5)×(4×2)=160(平方厘米)。

(4)111 提示:能看到的最小数是16,最大数是20,从16到20已经有连续的5个数了,那么第6个数是15或21。第一种情况:因为15+20=16+19=17+18,所以16和19在相对的面上,不符合题意;第二种情况:16+21=17+20=18+19,符合题意,这六个数的和是(17+20)×3=111。
(1)620 提示:包装带的总长度=4条长+4条宽+8条高+接头处的包装带长。50×4+40×4+30×8+20=620(厘米)。
(2)64 56 提示:长方体的左右侧面是正方形,且相交于同一顶点的三条棱中两条棱的长度分别是6厘米和4厘米,那么另一条棱长是6厘米或4厘米,则棱长和是6×8+4×4=64(厘米)或4×8+6×4=56(厘米)。
(3)160 提示:当正方体的展开图如图所示时,长方形纸的面积最小,是(4×5)×(4×2)=160(平方厘米)。

(4)111 提示:能看到的最小数是16,最大数是20,从16到20已经有连续的5个数了,那么第6个数是15或21。第一种情况:因为15+20=16+19=17+18,所以16和19在相对的面上,不符合题意;第二种情况:16+21=17+20=18+19,符合题意,这六个数的和是(17+20)×3=111。
8. 唐僧师徒欲对长20厘米、宽10厘米、高2厘米的长方体真经进行包装,悟空选择长30厘米、宽25厘米的彩纸,八戒选择长40厘米、宽13厘米的彩纸。谁选择的彩纸更合适?
答案:
悟空选择的彩纸更合适。 提示:彩纸的尺寸要能容下长方体真经展开图6个面所占的长、宽、高。长方体真经的展开图如图:

故彩纸的长和宽均要大于或等于24cm,因此悟空选择的彩纸更合适。
悟空选择的彩纸更合适。 提示:彩纸的尺寸要能容下长方体真经展开图6个面所占的长、宽、高。长方体真经的展开图如图:

故彩纸的长和宽均要大于或等于24cm,因此悟空选择的彩纸更合适。
9. (1)一个棱长和为80厘米的长方体,正好可以切成两个完全相同的小正方体,切成的每个小正方体的棱长和是( )。
(2)一个长方体木块正好可以切成3个完全相同的正方体,3个正方体的棱长总和比原来长方体的棱长和增加了160厘米,原来长方体的棱长和是( )。
(2)一个长方体木块正好可以切成3个完全相同的正方体,3个正方体的棱长总和比原来长方体的棱长和增加了160厘米,原来长方体的棱长和是( )。
答案:
(1)60厘米 提示:根据题意,可画出长方体如图。从图中可以看出,原来长方体的棱长和相当于正方体(8+8)条棱长的和。80÷(8+8)×12=60(厘米)。

(2)200厘米 提示:如图,将长方体木块切成3个完全相同的正方体,增加了4个切面,每个切面有4条正方体的棱长,所以切得的正方体棱长为160÷(4×4)=10(厘米)。原来长方体的棱长和是(30+10+10)×4=200(厘米)。

(1)60厘米 提示:根据题意,可画出长方体如图。从图中可以看出,原来长方体的棱长和相当于正方体(8+8)条棱长的和。80÷(8+8)×12=60(厘米)。

(2)200厘米 提示:如图,将长方体木块切成3个完全相同的正方体,增加了4个切面,每个切面有4条正方体的棱长,所以切得的正方体棱长为160÷(4×4)=10(厘米)。原来长方体的棱长和是(30+10+10)×4=200(厘米)。

10. 将一个正方体纸盒沿如图所示的线剪开,展开成平面图,其展开图的形状为(
B
)。答案:B 提示:由纸盒裁剪线可知,正方体展开图为两层,其下面、右面和上面正好被剪开,并位于同一层,而前面、左面和后面位于同一层,两层通过下面和后面连接起来,由此排除A、C两个选项,而D选项根本不能通过折叠围成正方体,故选项B正确。
11. 有序思想 如图,三种不同长度的小棒各有一些,用橡皮泥和这些小棒能搭出几种不同形状的长方体或正方体? (每次只取12根小棒)


答案:能搭出6种不同形状的长方体或正方体。
提示:列表如下。
①号小棒 ②号小棒 ③号小棒
根数 根数 根数
方法1 12 0 0
方法2 8 4 0
方法3 8 0 4
方法4 4 8 0
方法5 4 4 4
方法6 0 8 4
提示:列表如下。
①号小棒 ②号小棒 ③号小棒
根数 根数 根数
方法1 12 0 0
方法2 8 4 0
方法3 8 0 4
方法4 4 8 0
方法5 4 4 4
方法6 0 8 4