1. 计算下面各题。
$ \frac { 7 } { 1 0 } × 1 5 × \frac { 8 } { 2 1 } $
$ \frac { 5 } { 9 } × \frac { 7 } { 1 2 } × \frac { 1 8 } { 3 5 } $
$ \frac { 4 } { 1 1 } × \frac { 1 7 } { 1 8 } × \frac { 3 3 } { 3 4 } $
$ \frac { 7 } { 1 0 } × 1 5 × \frac { 8 } { 2 1 } $
4
$ \frac { 5 } { 9 } × \frac { 7 } { 1 2 } × \frac { 1 8 } { 3 5 } $
$\frac{1}{6}$
$ \frac { 4 } { 1 1 } × \frac { 1 7 } { 1 8 } × \frac { 3 3 } { 3 4 } $
$\frac{1}{3}$
答案:1. 4 $\frac{1}{6}$ $\frac{1}{3}$
解析:
$\frac{7}{10}×15×\frac{8}{21}$
$=\frac{7×15×8}{10×21}$
$=\frac{7×3×5×2×4}{2×5×3×7}$
$=4$
$\frac{5}{9}×\frac{7}{12}×\frac{18}{35}$
$=\frac{5×7×18}{9×12×35}$
$=\frac{5×7×2×9}{9×3×4×5×7}$
$=\frac{2}{12}$
$=\frac{1}{6}$
$\frac{4}{11}×\frac{17}{18}×\frac{33}{34}$
$=\frac{4×17×33}{11×18×34}$
$=\frac{4×17×3×11}{11×2×9×2×17}$
$=\frac{12}{36}$
$=\frac{1}{3}$
$=\frac{7×15×8}{10×21}$
$=\frac{7×3×5×2×4}{2×5×3×7}$
$=4$
$\frac{5}{9}×\frac{7}{12}×\frac{18}{35}$
$=\frac{5×7×18}{9×12×35}$
$=\frac{5×7×2×9}{9×3×4×5×7}$
$=\frac{2}{12}$
$=\frac{1}{6}$
$\frac{4}{11}×\frac{17}{18}×\frac{33}{34}$
$=\frac{4×17×33}{11×18×34}$
$=\frac{4×17×3×11}{11×2×9×2×17}$
$=\frac{12}{36}$
$=\frac{1}{3}$
2. (1)根据“甲是乙的$\frac {5}{8}$,丙是甲的$\frac {4}{5}$。”将数量关系式补全:(
(2)根据算式$70×\frac {6}{7}×\frac {2}{3}$补充条件:“古稀”“花甲”“不惑”等都是古代对年龄的称谓。“花甲”表示的年龄是“古稀”的$\frac {6}{7}$,______,“古稀”表示70岁,“不惑”表示多少岁?
乙
)$×\frac {5}{8}×\frac {4}{5}=$(丙
)。 (2)根据算式$70×\frac {6}{7}×\frac {2}{3}$补充条件:“古稀”“花甲”“不惑”等都是古代对年龄的称谓。“花甲”表示的年龄是“古稀”的$\frac {6}{7}$,______,“古稀”表示70岁,“不惑”表示多少岁?
“不惑”表示的年龄是“花甲”的$\frac{2}{3}$
答案:2.
(1)乙 丙
(2)“不惑”表示的年龄是“花甲”的$\frac{2}{3}$
(1)乙 丙
(2)“不惑”表示的年龄是“花甲”的$\frac{2}{3}$
$3. $明明家平均每天用水$ \frac { 3 } { 5 } $吨$,$开展节水活动后$,$每天比原来节约用水$ \frac { 1 } { 8 } 。$照这样计算$,$六月份可节约用水多少吨$?$
答案:3. $\frac{3}{5}×\frac{1}{8}×30=\frac{9}{4}$(吨)
$4. (1)$林凡写了四个数$,$其中甲数是乙数的$ \frac { 3 } { 5 } ,$乙数是丙数的$ \frac { 5 } { 4 } ,$丙数是丁数的$ \frac { 8 } { 1 5 } ,$甲数是丁数的 \frac {$ ($ $) $}$ ${$ ($ $) $}$ 。$
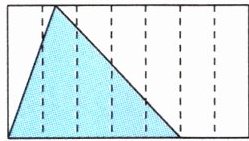
$(2)$如图$,$大长方形的面积是$28$平方分米$,$涂色部分三角形的面积是$($ $)$平方分米。
$(3)$一个皮球从$25$米的高处自由落下$,$接触地面后又立即弹起$,$再落下$,$又弹起$,$反复几次$,$每次弹起的高度是每次落下高度的$ \frac { 3 } { 5 } 。$第三次弹起的高度是$($ $)$米。
$(4)$水果店运来$450$千克苹果$,$第一天卖出$ \frac { 2 } { 5 } ,$第二天比第一天多卖出$ \frac { 1 } { 4 } ,$第二天比第一天多卖出$($ $)$千克苹果$,$两天一共卖出$($ $)$千克苹果。
$(5)$将$4$个棱长是$ \frac { 5 } { 6 } $分米的正方体拼成一个长方体$,$则表面积最少减少$($ $)$平方分米$,$最多减少$($ $)$平方分米。
$(6)$一个直角三角形的三条边分别长$ \frac { 3 } { 8 } $分米$, \frac { 1 } { 2 } $分米$, \frac { 5 } { 8 } $分米。直角三角形的面积是$($ $)$平方分米。如果把直角三角形的一条直角边延长到原来的$ \frac { 7 } { 3 } ,$另一条直角边缩短到原来的$ \frac { 2 } { 7 } ,$现在这个三角形的面积是$($ $)$平方分米。
$(7)$定义新运算:$ 1 \triangle 2 = \frac { 1 } { 1 } × \frac { 2 } { 2 } , 2 \triangle 4 = \frac { 1 } { 2 } × \frac { 2 } { 3 } × \frac { 3 } { 4 } × \frac { 4 } { 5 } , 3 \triangle 2 = \frac { 1 } { 3 } × \frac { 2 } { 4 } ,$那么$ 3 \triangle 5 = ($ $) 。$
$(2)$如图$,$大长方形的面积是$28$平方分米$,$涂色部分三角形的面积是$($ $)$平方分米。

$(3)$一个皮球从$25$米的高处自由落下$,$接触地面后又立即弹起$,$再落下$,$又弹起$,$反复几次$,$每次弹起的高度是每次落下高度的$ \frac { 3 } { 5 } 。$第三次弹起的高度是$($ $)$米。
$(4)$水果店运来$450$千克苹果$,$第一天卖出$ \frac { 2 } { 5 } ,$第二天比第一天多卖出$ \frac { 1 } { 4 } ,$第二天比第一天多卖出$($ $)$千克苹果$,$两天一共卖出$($ $)$千克苹果。
$(5)$将$4$个棱长是$ \frac { 5 } { 6 } $分米的正方体拼成一个长方体$,$则表面积最少减少$($ $)$平方分米$,$最多减少$($ $)$平方分米。
$(6)$一个直角三角形的三条边分别长$ \frac { 3 } { 8 } $分米$, \frac { 1 } { 2 } $分米$, \frac { 5 } { 8 } $分米。直角三角形的面积是$($ $)$平方分米。如果把直角三角形的一条直角边延长到原来的$ \frac { 7 } { 3 } ,$另一条直角边缩短到原来的$ \frac { 2 } { 7 } ,$现在这个三角形的面积是$($ $)$平方分米。
$(7)$定义新运算:$ 1 \triangle 2 = \frac { 1 } { 1 } × \frac { 2 } { 2 } , 2 \triangle 4 = \frac { 1 } { 2 } × \frac { 2 } { 3 } × \frac { 3 } { 4 } × \frac { 4 } { 5 } , 3 \triangle 2 = \frac { 1 } { 3 } × \frac { 2 } { 4 } ,$那么$ 3 \triangle 5 = ($ $) 。$
答案:
4.
(1)$\frac{2}{5}$
(2)10
(3)$\frac{27}{5}$
(4)45 405 提示:由题意可知,第二天比第一天多卖出$450×\frac{2}{5}×\frac{1}{4}=45$(千克)。求两天一共卖出多少千克苹果,需要将两天卖出的苹果数量相加,需注意的是第二天卖出的苹果数量是第一天卖出的数量加上第二天比第一天多卖的数量,即$450×\frac{2}{5}×2+45=405$(千克)。
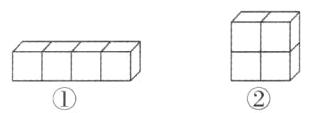
(5)$\frac{25}{6}$ $\frac{50}{9}$ 提示:4个正方体可以排成一排(如图①),重合了3次,减少了6个面,减少的面积=一个面的面积×6=$\frac{5}{6}×\frac{5}{6}×6=\frac{25}{6}$(平方分米);也可以排成两行两列(如图②),重合了4次,减少了8个面,减少的面积=一个面的面积×8=$\frac{5}{6}×\frac{5}{6}×8=\frac{50}{9}$(平方分米)。
(6)$\frac{3}{32}$ $\frac{1}{16}$ 提示:直角三角形中斜边最长,所以长$\frac{3}{8}$分米和$\frac{1}{2}$分米的两条边为直角边,再根据直角三角形的面积等于两条直角边乘积的一半来列式计算,列式为$\frac{1}{2}×\frac{3}{8}×\frac{1}{2}=\frac{3}{32}$(平方分米)。直角三角形的面积会随着两条直角边的变化也发生同样的变化。现在这个三角形的面积是$\frac{3}{32}×\frac{7}{3}×\frac{2}{7}=\frac{1}{16}$(平方分米)。
(7)$\frac{1}{21}$ 提示:由给出的定义可知,$3△5=\frac{1}{3}×\frac{2}{4}×\frac{3}{5}×\frac{4}{6}×\frac{5}{7}=\frac{1}{21}$。
4.
(1)$\frac{2}{5}$
(2)10
(3)$\frac{27}{5}$
(4)45 405 提示:由题意可知,第二天比第一天多卖出$450×\frac{2}{5}×\frac{1}{4}=45$(千克)。求两天一共卖出多少千克苹果,需要将两天卖出的苹果数量相加,需注意的是第二天卖出的苹果数量是第一天卖出的数量加上第二天比第一天多卖的数量,即$450×\frac{2}{5}×2+45=405$(千克)。
(5)$\frac{25}{6}$ $\frac{50}{9}$ 提示:4个正方体可以排成一排(如图①),重合了3次,减少了6个面,减少的面积=一个面的面积×6=$\frac{5}{6}×\frac{5}{6}×6=\frac{25}{6}$(平方分米);也可以排成两行两列(如图②),重合了4次,减少了8个面,减少的面积=一个面的面积×8=$\frac{5}{6}×\frac{5}{6}×8=\frac{50}{9}$(平方分米)。

(6)$\frac{3}{32}$ $\frac{1}{16}$ 提示:直角三角形中斜边最长,所以长$\frac{3}{8}$分米和$\frac{1}{2}$分米的两条边为直角边,再根据直角三角形的面积等于两条直角边乘积的一半来列式计算,列式为$\frac{1}{2}×\frac{3}{8}×\frac{1}{2}=\frac{3}{32}$(平方分米)。直角三角形的面积会随着两条直角边的变化也发生同样的变化。现在这个三角形的面积是$\frac{3}{32}×\frac{7}{3}×\frac{2}{7}=\frac{1}{16}$(平方分米)。
(7)$\frac{1}{21}$ 提示:由给出的定义可知,$3△5=\frac{1}{3}×\frac{2}{4}×\frac{3}{5}×\frac{4}{6}×\frac{5}{7}=\frac{1}{21}$。
$5. $计算:$ ( 1 + \frac { 1 } { 2 } ) × ( 1 - \frac { 1 } { 2 } ) × ( 1 + \frac { 1 } { 3 } ) × ( 1 - \frac { 1 } { 3 } ) × … × ( 1 + \frac { 1 } { 9 9 } ) × ( 1 - \frac { 1 } { 9 9 } ) 。$
答案:5. $(1+\frac{1}{2})×(1-\frac{1}{2})×(1+\frac{1}{3})×(1-\frac{1}{3})×... ×(1+\frac{1}{99})×(1-\frac{1}{99})=\frac{3}{2}×\frac{1}{2}×\frac{4}{3}×\frac{2}{3}×... ×\frac{100}{99}×\frac{98}{99}=(\frac{3}{2}×\frac{2}{3})×(\frac{4}{3}×\frac{3}{4})×... ×(\frac{99}{98}×\frac{98}{99})×(\frac{1}{2}×\frac{100}{99})=\frac{1}{2}×\frac{100}{99}=\frac{50}{99}$ 提示:计算本题时,可以先算出每个小括号里的结果,然后通过仔细观察,把乘积是1的两个因数进行两两配对,这样可以使计算简便。