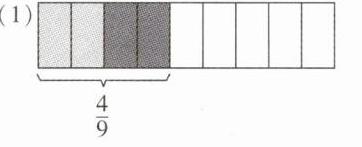
1. (1)先画图表示计算过程,再计算。
$\frac {4}{9}÷2$
方法一:$\frac {4}{9}÷2= \frac {(4)÷(2)}{(9)}= (\frac{2}{9})$
方法二:$\frac {4}{9}÷2= \frac {4}{9}×\frac {(1)}{(2)}= (\frac{2}{9})$
(2)修一条长$\frac {3}{5}$千米的路,6天修完,平均每天修(
$\frac {4}{9}÷2$

方法一:$\frac {4}{9}÷2= \frac {(4)÷(2)}{(9)}= (\frac{2}{9})$
方法二:$\frac {4}{9}÷2= \frac {4}{9}×\frac {(1)}{(2)}= (\frac{2}{9})$
(2)修一条长$\frac {3}{5}$千米的路,6天修完,平均每天修(
$\frac{1}{10}$
)千米,平均每天修这条路的($\frac{1}{6}$
)。答案:
1.
(1)方法一:$\frac{4÷2}{9}=\frac{2}{9}$ 方法二:$\frac{4}{9}×\frac{1}{2}=\frac{2}{9}$
(2)$\frac{1}{10}$,$\frac{1}{6}$
1.

(1)方法一:$\frac{4÷2}{9}=\frac{2}{9}$ 方法二:$\frac{4}{9}×\frac{1}{2}=\frac{2}{9}$
(2)$\frac{1}{10}$,$\frac{1}{6}$
2. $\frac {15}{16}÷10=$
$\frac {12}{13}÷4=$
$\frac{3}{32}$
$\frac {14}{25}÷21=$$\frac{2}{75}$
$\frac {12}{13}÷4=$
$\frac{3}{13}$
$\frac {33}{35}÷22=$$\frac{3}{70}$
答案:$\frac{3}{32}$,$\frac{2}{75}$,$\frac{3}{13}$,$\frac{3}{70}$
解析:
$\frac{15}{16}÷10=\frac{15}{16}×\frac{1}{10}=\frac{3}{32}$,$\frac{14}{25}÷21=\frac{14}{25}×\frac{1}{21}=\frac{2}{75}$,$\frac{12}{13}÷4=\frac{12}{13}×\frac{1}{4}=\frac{3}{13}$,$\frac{33}{35}÷22=\frac{33}{35}×\frac{1}{22}=\frac{3}{70}$
3. 能够表示图中斜线部分的算式是(
A.$\frac {3}{5}÷3$
B.$\frac {4}{5}÷3$
C.$\frac {3}{5}÷4$
D.$\frac {4}{5}÷4$
B
)。A.$\frac {3}{5}÷3$
B.$\frac {4}{5}÷3$
C.$\frac {3}{5}÷4$
D.$\frac {4}{5}÷4$
答案:B
解析:
图中整体被平均分成5列,浅色阴影部分占4列,即浅色阴影部分为整体的$\frac{4}{5}$。斜线部分是将浅色阴影部分平均分成3份后的1份,所以斜线部分表示的算式是$\frac{4}{5}÷3$。
B
B
4. (1)若$a×\frac {1}{3}= b÷4$,则$a◯ b$。$(a、b$均不为 0)
(2)括号里能填整数几?
$\frac {( )}{15}÷6= \frac {7}{( )}$
(3)如图,已知点 A 在$\frac {1}{5}$处,点 B 在$\frac {4}{5}$处,C是线段 AB 的中点。点 C 表示的数是$\frac {( )}{( )}$。
(4)已知$◯ ÷4= ☆,◯ -☆= \frac {18}{25}$,则$◯ =( ),☆= ( )$。
<
(2)括号里能填整数几?
$\frac {( )}{15}÷6= \frac {7}{( )}$
7
90
$\frac {8}{( )}÷5= \frac {( )}{35}$7
8
(3)如图,已知点 A 在$\frac {1}{5}$处,点 B 在$\frac {4}{5}$处,C是线段 AB 的中点。点 C 表示的数是$\frac {( )}{( )}$。
1
2
(4)已知$◯ ÷4= ☆,◯ -☆= \frac {18}{25}$,则$◯ =( ),☆= ( )$。
$\frac{24}{25}$
$\frac{6}{25}$
答案:
(1)<
(2)答案不唯一,如:7 90 7 8
(3)$\frac{1}{2}$
(4)$\frac{24}{25}$,$\frac{6}{25}$
(1)<
(2)答案不唯一,如:7 90 7 8
(3)$\frac{1}{2}$
(4)$\frac{24}{25}$,$\frac{6}{25}$
5. (1)一瓶饮料$\frac {3}{2}$升,平均倒满3个同样的杯子后,还剩这瓶饮料的$\frac {3}{5}$,平均每个杯子倒了这瓶饮料的$\frac {
(2)施工队修建一条长$\frac {24}{25}$千米的高速公路,3天共修建了全长的一半,平均每天修建$
(3)一根长方体木料长2米,截成3段后,表面积增加$\frac {8}{9}$平方米。原来这根木料的横截面的面积是$
(4)李君在计算一个数除以3时,错把除以3看成了乘3,结果是$\frac {18}{19}$。这道除法算式的正确结果是$
2
}{15
}$。(2)施工队修建一条长$\frac {24}{25}$千米的高速公路,3天共修建了全长的一半,平均每天修建$
\frac{4}{25}
$千米。(3)一根长方体木料长2米,截成3段后,表面积增加$\frac {8}{9}$平方米。原来这根木料的横截面的面积是$
\frac{2}{9}
$平方米。(4)李君在计算一个数除以3时,错把除以3看成了乘3,结果是$\frac {18}{19}$。这道除法算式的正确结果是$
\frac{2}{19}
$。答案:
(1)$\frac{2}{15}$ 提示:用$1 - \frac{3}{5}$求出倒掉了这瓶饮料的$\frac{2}{5}$,平均倒满3个同样的杯子,平均每个杯子倒了这瓶饮料的$\frac{2}{5}÷3 = \frac{2}{15}$。
(2)$\frac{4}{25}$ 提示:求$\frac{24}{25}$的一半用$\frac{24}{25}÷2$,用得数再除以3就能求出平均每天修建的千米数。
(3)$\frac{2}{9}$ 提示:将木料截成3段,需要截两次,表面积增加了$2×2 = 4$(个)横截面的面积,用增加的表面积除以4即可求出横截面的面积为$\frac{8}{9}÷4 = \frac{2}{9}$(平方米)。
(4)$\frac{2}{19}$ 提示:采用将错就错法来解,根据“一个数$×3 = \frac{18}{19}$”,求出这个数是$\frac{18}{19}÷3 = \frac{6}{19}$,再求出正确的结果是$\frac{6}{19}÷3 = \frac{2}{19}$。
(1)$\frac{2}{15}$ 提示:用$1 - \frac{3}{5}$求出倒掉了这瓶饮料的$\frac{2}{5}$,平均倒满3个同样的杯子,平均每个杯子倒了这瓶饮料的$\frac{2}{5}÷3 = \frac{2}{15}$。
(2)$\frac{4}{25}$ 提示:求$\frac{24}{25}$的一半用$\frac{24}{25}÷2$,用得数再除以3就能求出平均每天修建的千米数。
(3)$\frac{2}{9}$ 提示:将木料截成3段,需要截两次,表面积增加了$2×2 = 4$(个)横截面的面积,用增加的表面积除以4即可求出横截面的面积为$\frac{8}{9}÷4 = \frac{2}{9}$(平方米)。
(4)$\frac{2}{19}$ 提示:采用将错就错法来解,根据“一个数$×3 = \frac{18}{19}$”,求出这个数是$\frac{18}{19}÷3 = \frac{6}{19}$,再求出正确的结果是$\frac{6}{19}÷3 = \frac{2}{19}$。
6. 乐乐在计算$\frac {3}{4}$、$\frac {4}{5}$、$\frac {5}{6}$、$\frac {8}{9}$这四个分数的平均数时,不小心把其中一个分数的分子、分母写颠倒了,这样他所计算出的平均数和正确的平均数最大相差多少?
答案:$\frac{4}{3}-\frac{3}{4}=\frac{7}{12}$,$\frac{5}{4}-\frac{4}{5}=\frac{9}{20}$,$\frac{6}{5}-\frac{5}{6}=\frac{11}{30}$,$\frac{9}{8}-\frac{8}{9}=\frac{17}{72}$ 因为$\frac{17}{72}<\frac{11}{30}<\frac{9}{20}<\frac{7}{12}$,所以最大的差是$\frac{7}{12}$。 平均数最大相差$\frac{7}{12}÷4=\frac{7}{48}$ 提示:解题时,应结合给出的分数进行计算,找出哪个分数分子和分母写颠倒后,相差最大,进而根据平均数的求法解答即可。
解析:
分别计算每个分数分子分母颠倒后的差:
$\frac{4}{3} - \frac{3}{4} = \frac{16}{12} - \frac{9}{12} = \frac{7}{12}$
$\frac{5}{4} - \frac{4}{5} = \frac{25}{20} - \frac{16}{20} = \frac{9}{20}$
$\frac{6}{5} - \frac{5}{6} = \frac{36}{30} - \frac{25}{30} = \frac{11}{30}$
$\frac{9}{8} - \frac{8}{9} = \frac{81}{72} - \frac{64}{72} = \frac{17}{72}$
比较差的大小:$\frac{17}{72} < \frac{11}{30} < \frac{9}{20} < \frac{7}{12}$,最大差为$\frac{7}{12}$。
平均数最大相差:$\frac{7}{12} ÷ 4 = \frac{7}{12} × \frac{1}{4} = \frac{7}{48}$
$\frac{7}{48}$
$\frac{4}{3} - \frac{3}{4} = \frac{16}{12} - \frac{9}{12} = \frac{7}{12}$
$\frac{5}{4} - \frac{4}{5} = \frac{25}{20} - \frac{16}{20} = \frac{9}{20}$
$\frac{6}{5} - \frac{5}{6} = \frac{36}{30} - \frac{25}{30} = \frac{11}{30}$
$\frac{9}{8} - \frac{8}{9} = \frac{81}{72} - \frac{64}{72} = \frac{17}{72}$
比较差的大小:$\frac{17}{72} < \frac{11}{30} < \frac{9}{20} < \frac{7}{12}$,最大差为$\frac{7}{12}$。
平均数最大相差:$\frac{7}{12} ÷ 4 = \frac{7}{12} × \frac{1}{4} = \frac{7}{48}$
$\frac{7}{48}$