9. 电脑公司第一天装配了 75 台电脑,第二天装配了 65 台电脑,两天装配的电脑总数相当于总量的$\frac{2}{5}$,经理说第一天装配了总量的$\frac{3}{14}$,他说得对吗?
答案:$75+65=140$(台) $140÷\frac{2}{5}×\frac{3}{14}=75$(台)
他说得对。 提示:先用第一天装配的75台电脑加第二天装配的65台电脑,求出两天共装配了140台电脑,再用$140÷\frac{2}{5}$求出电脑总数,用电脑总数乘$\frac{3}{14}$,看结果是否与第一天装配的75台电脑一致。
他说得对。 提示:先用第一天装配的75台电脑加第二天装配的65台电脑,求出两天共装配了140台电脑,再用$140÷\frac{2}{5}$求出电脑总数,用电脑总数乘$\frac{3}{14}$,看结果是否与第一天装配的75台电脑一致。
10. 甲、乙两个粮仓,甲粮仓的大米是乙粮仓的$\frac{3}{5}$,从乙粮仓运 12 吨大米给甲粮仓,两个粮仓的大米就同样多,原来乙粮仓有多少吨大米?
答案:$1-\frac{3}{5}=\frac{2}{5}$ $12×2÷\frac{2}{5}=60$(吨) 提示:从乙粮仓运12吨大米给甲粮仓,两个粮仓的大米就同样多,则乙粮仓比甲粮仓多$12×2=24$(吨)大米,又甲粮仓的大米是乙粮仓的$\frac{3}{5}$,则甲粮仓比乙粮仓少$1-\frac{3}{5}=\frac{2}{5}$,即24吨占乙粮仓吨数的分率是$\frac{2}{5}$,所以乙粮仓有大米$24÷\frac{2}{5}=60$(吨)。
解析:
乙粮仓比甲粮仓多的吨数:$12×2 = 24$(吨)
甲粮仓比乙粮仓少的分率:$1-\frac{3}{5}=\frac{2}{5}$
原来乙粮仓的吨数:$24÷\frac{2}{5}=60$(吨)
答:原来乙粮仓有60吨大米。
甲粮仓比乙粮仓少的分率:$1-\frac{3}{5}=\frac{2}{5}$
原来乙粮仓的吨数:$24÷\frac{2}{5}=60$(吨)
答:原来乙粮仓有60吨大米。
11. 乐乐在计算一个数乘$\frac{2}{3}$,再除以$\frac{4}{3}$时,错把乘算成了除,把除算成了乘,得到错误结果 30,正确的结果是几?
答案:$30÷\frac{4}{3}×\frac{2}{3}=15$ $15×\frac{2}{3}÷\frac{4}{3}=\frac{15}{2}$ 提示:将错就错,由题意可知,一个数$÷\frac{2}{3}×\frac{4}{3}=30$,这个数=$30÷\frac{4}{3}×\frac{2}{3}=15$,正确的结果是$15×\frac{2}{3}÷\frac{4}{3}=\frac{15}{2}$。
解析:
设这个数为$x$。
因为乐乐错把乘算成除,把除算成乘,所以错误的算式为$x÷\frac{2}{3}×\frac{4}{3}=30$。
则$x=30÷\frac{4}{3}×\frac{2}{3}$
$=30×\frac{3}{4}×\frac{2}{3}$
$=30×\frac{1}{2}$
$=15$。
正确的算式为$15×\frac{2}{3}÷\frac{4}{3}$
$=10÷\frac{4}{3}$
$=10×\frac{3}{4}$
$=\frac{15}{2}$。
$\frac{15}{2}$
因为乐乐错把乘算成除,把除算成乘,所以错误的算式为$x÷\frac{2}{3}×\frac{4}{3}=30$。
则$x=30÷\frac{4}{3}×\frac{2}{3}$
$=30×\frac{3}{4}×\frac{2}{3}$
$=30×\frac{1}{2}$
$=15$。
正确的算式为$15×\frac{2}{3}÷\frac{4}{3}$
$=10÷\frac{4}{3}$
$=10×\frac{3}{4}$
$=\frac{15}{2}$。
$\frac{15}{2}$
12. 有一桶水和几个同样大小的瓶子,若装满 8 瓶,则用去桶里水的$\frac{1}{7}$;若装满 7 瓶,则用去 6 千克水,这桶水有多少千克?
答案:$6÷7=\frac{6}{7}$(千克) $\frac{6}{7}×8÷\frac{1}{7}=48$(千克)
提示:根据“装满7瓶,用去6千克水”,可求出每瓶水的质量;然后根据“装满8瓶,用去桶里水的$\frac{1}{7}$”,可求出8瓶水的质量,进而求出这桶水的质量。
提示:根据“装满7瓶,用去6千克水”,可求出每瓶水的质量;然后根据“装满8瓶,用去桶里水的$\frac{1}{7}$”,可求出8瓶水的质量,进而求出这桶水的质量。
13. 如图,一辆快车和一辆慢车分别从甲、乙两地同时相对开出,3 小时后相遇,相遇点与甲、乙两地中点的距离占全程的$\frac{1}{7}$。已知快车比慢车每小时多行 60 千米,求甲、乙两地之间的距离。
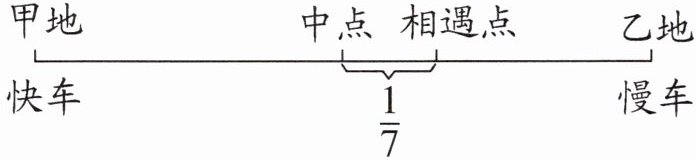

答案:$60×3=180$(千米) $\frac{1}{7}×2=\frac{2}{7}$ $180÷\frac{2}{7}=630$(千米) 提示:相遇时,快车比慢车多行了$60×3=180$(千米),快车比慢车多行的路程占全程的$(\frac{1}{7}×2)$。
解析:
$60×3=180$(千米)
$\frac{1}{7}×2=\frac{2}{7}$
$180÷\frac{2}{7}=630$(千米)
答:甲、乙两地之间的距离为$630$千米。
$\frac{1}{7}×2=\frac{2}{7}$
$180÷\frac{2}{7}=630$(千米)
答:甲、乙两地之间的距离为$630$千米。
14. 一瓶油用去$\frac{1}{3}$后,余下的油连瓶重 900 克,再用去余下油
的
$\frac{3}{4}$后,余下的油连瓶重 450 克。瓶中原有油多少克?答案:$1-\frac{1}{3}=\frac{2}{3}$ $900-450=450$(克)
$450÷\frac{3}{4}÷\frac{2}{3}=900$(克) 提示:第二次用去$(900-450)$克油,占第一次用去后余下油的$\frac{3}{4}$,根据第一次用去后余下油的克数$×\frac{3}{4}=$第二次用去油的克数这一数量关系式,可求出第一次用去后余下油的克数。由于第一次用去整瓶油的$\frac{1}{3}$,所以第一次用去后余下油的克数占整瓶油的$(1-\frac{1}{3})$,根据整瓶油的克数$×(1-\frac{1}{3})=$第一次用去后余下油的克数这一数量关系式,可求出整瓶油的克数。
$450÷\frac{3}{4}÷\frac{2}{3}=900$(克) 提示:第二次用去$(900-450)$克油,占第一次用去后余下油的$\frac{3}{4}$,根据第一次用去后余下油的克数$×\frac{3}{4}=$第二次用去油的克数这一数量关系式,可求出第一次用去后余下油的克数。由于第一次用去整瓶油的$\frac{1}{3}$,所以第一次用去后余下油的克数占整瓶油的$(1-\frac{1}{3})$,根据整瓶油的克数$×(1-\frac{1}{3})=$第一次用去后余下油的克数这一数量关系式,可求出整瓶油的克数。
15. 3 只猴子摘桃,第 1 只猴子摘的个数是其余两只猴子摘桃总数的$\frac{1}{2}$,第 2 只猴子摘的个数是其余两只猴子摘桃总数的$\frac{2}{7}$,第 3 只猴子摘了 24 个桃。它们一共摘了多少个桃?
答案:$\frac{2}{3}+\frac{7}{9}-1=\frac{4}{9}$ $24÷\frac{4}{9}=54$(个) 提示:第1只猴子摘的个数是其余两只猴子摘桃总数的$\frac{1}{2}$,说明第2只猴子和第3只猴子摘的桃子个数占总个数的$\frac{2}{3}$,同理,第1只猴子和第3只猴子摘的桃子个数占总个数的$\frac{7}{9}$,所以第3只猴子摘的桃子个数占总个数的$\frac{2}{3}+\frac{7}{9}-1=\frac{4}{9}$,进而求出它们一共摘的桃子个数。
解析:
第1只猴子摘的个数是其余两只猴子摘桃总数的$\frac{1}{2}$,则第2只和第3只猴子摘的桃子个数占总个数的$\frac{2}{1+2}=\frac{2}{3}$。
第2只猴子摘的个数是其余两只猴子摘桃总数的$\frac{2}{7}$,则第1只和第3只猴子摘的桃子个数占总个数的$\frac{7}{2+7}=\frac{7}{9}$。
第3只猴子摘的桃子个数占总个数的$\frac{2}{3}+\frac{7}{9}-1=\frac{6}{9}+\frac{7}{9}-\frac{9}{9}=\frac{4}{9}$。
它们一共摘桃的个数为$24÷\frac{4}{9}=24×\frac{9}{4}=54$(个)。
答:它们一共摘了54个桃。
第2只猴子摘的个数是其余两只猴子摘桃总数的$\frac{2}{7}$,则第1只和第3只猴子摘的桃子个数占总个数的$\frac{7}{2+7}=\frac{7}{9}$。
第3只猴子摘的桃子个数占总个数的$\frac{2}{3}+\frac{7}{9}-1=\frac{6}{9}+\frac{7}{9}-\frac{9}{9}=\frac{4}{9}$。
它们一共摘桃的个数为$24÷\frac{4}{9}=24×\frac{9}{4}=54$(个)。
答:它们一共摘了54个桃。