1. (1)$4÷5=$
(2)一本童话书共150页,已经看了90页。已看的页数与总页数的比是
(3)王阿姨买3千克苹果用去22.5元,苹果的总价与数量的比是
(4)正方形A的边长是1米,正方形B的边长是3米,A与B的边长比是
4
:5
= $\frac{4
}{5
}$(2)一本童话书共150页,已经看了90页。已看的页数与总页数的比是
90:150
,剩下的页数与总页数的比是60:150
,已看的页数与剩下的页数的比是90:60
。(3)王阿姨买3千克苹果用去22.5元,苹果的总价与数量的比是
22.5:3
,比值是7.5
,这个比值表示每千克苹果的售价
。(4)正方形A的边长是1米,正方形B的边长是3米,A与B的边长比是
1:3
,周长比是4:12
,面积比是1:9
。答案:1.
(1)4 5 $\frac{4}{5}$
(2)90:150 60:150 90:60
(3)22.5:3 7.5 每千克苹果的售价
(4)1:3 4:12 1:9
(1)4 5 $\frac{4}{5}$
(2)90:150 60:150 90:60
(3)22.5:3 7.5 每千克苹果的售价
(4)1:3 4:12 1:9
2. 求下面各比的比值。
$\frac{5}{6}:10$ $0.6:0.75$ $\frac{2}{5}$千克 : 800克
$\frac{5}{6}:10$ $0.6:0.75$ $\frac{2}{5}$千克 : 800克
答案:2.$\frac{1}{12}$ $\frac{4}{5}$ $\frac{1}{2}$
解析:
$\frac{5}{6}:10=\frac{5}{6}÷10=\frac{5}{6}×\frac{1}{10}=\frac{1}{12}$
$0.6:0.75=60:75=\frac{60}{75}=\frac{4}{5}$
$\frac{2}{5}$千克$:800$克$=400$克$:800$克$=400÷800=\frac{1}{2}$
$0.6:0.75=60:75=\frac{60}{75}=\frac{4}{5}$
$\frac{2}{5}$千克$:800$克$=400$克$:800$克$=400÷800=\frac{1}{2}$
(1)$\frac{5}{8}$可看作是一个比,读作5比8。(
(2)一场足球比赛的比分是$3:0$,说明比的后项可以是0。(
(3)一杯盐水中盐与水的比是$1:10$,喝掉一半后,盐与水的比是$1:5$。(
(4)a比b多$\frac{1}{5}$,a与b的比是$6:5$。(
(5)张师傅5分钟加工了3个零件,李师傅8分钟加工了5个零件,张师傅和李师傅每分钟加工零件个数的比是$25:24$。(
√
)(2)一场足球比赛的比分是$3:0$,说明比的后项可以是0。(
×
)(3)一杯盐水中盐与水的比是$1:10$,喝掉一半后,盐与水的比是$1:5$。(
×
)(4)a比b多$\frac{1}{5}$,a与b的比是$6:5$。(
√
)(5)张师傅5分钟加工了3个零件,李师傅8分钟加工了5个零件,张师傅和李师傅每分钟加工零件个数的比是$25:24$。(
×
)答案:3.
(1)√
(2)×
(3)×
(4)√
(5)×
(1)√
(2)×
(3)×
(4)√
(5)×
4. (1)甲数除以乙数的商是0.7,那么乙数与甲数的比是
(2)甲、乙两人都从A地到B地,甲走了1小时,乙走了50分钟。甲与乙的速度比是
(3)钟面上,分针与秒针的转动速度的比是
(4)有大、小两筐苹果,从大筐里拿出$\frac{2}{7}$到小筐,则两筐苹果的质量相等,原来大、小两筐苹果的质量比是
(5)A种糖水中糖与水的质量比是$1:9$,B种糖水中糖占糖水的$\frac{1}{9}$,
10:7
;被减数与减数的比是$13:9$,那么减数与差的比是9:4
。(2)甲、乙两人都从A地到B地,甲走了1小时,乙走了50分钟。甲与乙的速度比是
5:6
。(3)钟面上,分针与秒针的转动速度的比是
1:60
。(4)有大、小两筐苹果,从大筐里拿出$\frac{2}{7}$到小筐,则两筐苹果的质量相等,原来大、小两筐苹果的质量比是
7:3
;如果大筐里的苹果卖出$\frac{3}{5}$后就和小筐里的苹果质量相等,那么原来大、小两筐苹果的质量比是5:2
。(5)A种糖水中糖与水的质量比是$1:9$,B种糖水中糖占糖水的$\frac{1}{9}$,
B
种糖水甜一些。答案:4.
(1)10:7 9:4 提示:甲数÷乙数=0.7=$\frac{7}{10}$,甲数是7份,乙数是10份,乙数:甲数=10:7。被减数与减数的比是13:9,把被减数看作13份,减数看作9份,则差是4份,所以减数与差的比是9:4。
(2)5:6 提示:把A、B两地的距离看作单位“1”,则甲的速度为1,50分钟=$\frac{5}{6}$小时,乙的速度为1÷$\frac{5}{6}$=$\frac{6}{5}$,依据比的意义可求出甲与乙的速度比为1:$\frac{6}{5}$=5:6。
(3)1:60 提示:钟面上,分针1分钟走1小格,秒针1分钟走一圈,也就是60小格,所以分针与秒针的转动速度比是1:60。
(4)7:3 5:2 提示:从大筐里拿出$\frac{2}{7}$到小筐,则两筐苹果的质量相等,即原来小筐里的苹果质量比大筐少$\frac{2}{7}$×2=$\frac{4}{7}$,把原来大筐里的苹果质量平均分成7份,小筐里的苹果质量就是3份,所以原来大、小两筐苹果的质量比是7:3。大筐里的苹果卖出$\frac{3}{5}$后就和小筐里的苹果质量相等,把原来大筐里的苹果质量平均分成5份,卖出3份后,还剩2份,也就是小筐里的苹果质量,所以原来大、小两筐苹果的质量比是5:2。
(5)B 提示:A种糖水中糖占糖水的1÷(1+9)=$\frac{1}{10}$,$\frac{1}{10}$<$\frac{1}{9}$,B种糖水甜一些。
(1)10:7 9:4 提示:甲数÷乙数=0.7=$\frac{7}{10}$,甲数是7份,乙数是10份,乙数:甲数=10:7。被减数与减数的比是13:9,把被减数看作13份,减数看作9份,则差是4份,所以减数与差的比是9:4。
(2)5:6 提示:把A、B两地的距离看作单位“1”,则甲的速度为1,50分钟=$\frac{5}{6}$小时,乙的速度为1÷$\frac{5}{6}$=$\frac{6}{5}$,依据比的意义可求出甲与乙的速度比为1:$\frac{6}{5}$=5:6。
(3)1:60 提示:钟面上,分针1分钟走1小格,秒针1分钟走一圈,也就是60小格,所以分针与秒针的转动速度比是1:60。
(4)7:3 5:2 提示:从大筐里拿出$\frac{2}{7}$到小筐,则两筐苹果的质量相等,即原来小筐里的苹果质量比大筐少$\frac{2}{7}$×2=$\frac{4}{7}$,把原来大筐里的苹果质量平均分成7份,小筐里的苹果质量就是3份,所以原来大、小两筐苹果的质量比是7:3。大筐里的苹果卖出$\frac{3}{5}$后就和小筐里的苹果质量相等,把原来大筐里的苹果质量平均分成5份,卖出3份后,还剩2份,也就是小筐里的苹果质量,所以原来大、小两筐苹果的质量比是5:2。
(5)B 提示:A种糖水中糖占糖水的1÷(1+9)=$\frac{1}{10}$,$\frac{1}{10}$<$\frac{1}{9}$,B种糖水甜一些。
5. 已知A、B是1~100中的两个不同自然数,则$(A+B):(A-B)$的比值最大是(
199
)。答案:5.199 提示:要使比值最大,则比的前项应尽可能大,而比的后项应尽可能小。根据“A、B是1~100中的两个不同自然数”可知,这两个自然数的和最大是199,差最小是1,即A=100,B=99。
解析:
要使$(A+B):(A-B)$的比值最大,需使前项$A+B$尽可能大,后项$A-B$尽可能小。
因为$A$、$B$是1~100中的不同自然数,所以$A+B$的最大值为$100 + 99 = 199$,$A-B$的最小值为$1$(此时$A=100$,$B=99$)。
因此,$(A+B):(A-B)=199:1=199$。
199
因为$A$、$B$是1~100中的不同自然数,所以$A+B$的最大值为$100 + 99 = 199$,$A-B$的最小值为$1$(此时$A=100$,$B=99$)。
因此,$(A+B):(A-B)=199:1=199$。
199
6. 如图,用7个相同的小长方形正好拼成一个大长方形,每个小长方形的长和宽的比是(
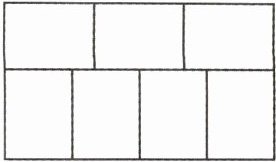
4:3
),大长方形的长和宽的比是(12:7
)。
答案:6.4:3 12:7 提示:从题图中可知,小长方形的长×3=小长方形的宽×4,设两边乘积都等于12,则小长方形的长与宽的比是4:3,大长方形的长与宽的比是12:7。
解析:
设小长方形的长为$a$,宽为$b$。由图可知,$3a = 4b$,则$a:b = 4:3$。
大长方形的长为$3a$,宽为$a + b$。因为$a:b = 4:3$,设$a = 4k$,$b = 3k$($k$为正数),所以大长方形的宽为$4k + 3k = 7k$,长为$3×4k = 12k$,故大长方形长和宽的比是$12k:7k = 12:7$。
4:3;12:7
大长方形的长为$3a$,宽为$a + b$。因为$a:b = 4:3$,设$a = 4k$,$b = 3k$($k$为正数),所以大长方形的宽为$4k + 3k = 7k$,长为$3×4k = 12k$,故大长方形长和宽的比是$12k:7k = 12:7$。
4:3;12:7