1. (1)$3:4= ($
(2) 小芳的身高是 1.2 米,妈妈的身高是 160 厘米,小芳身高与妈妈身高的最简单的整数比是($
(3) 把$24:36$的后项除以 12,则前项要改为($
9
$):12= 15÷($20
$)= \frac{($21
$)}{28}$(2) 小芳的身高是 1.2 米,妈妈的身高是 160 厘米,小芳身高与妈妈身高的最简单的整数比是($
3:4
$)。(3) 把$24:36$的后项除以 12,则前项要改为($
2
$),比值才不变。答案:1.
(1)9 20 21
(2)3:4
(3)2
(1)9 20 21
(2)3:4
(3)2
2. 判断题。
(1) 把$5:2.5$化成最简单的整数比是 2。 (
(2) 平行四边形底与高的比是$5:4$,说明平行四边形的底是 5 分米,高是 4 分米。 (
(3) 一个比的前项乘 0.5,后项除以 2,则比值不变。 (
(1) 把$5:2.5$化成最简单的整数比是 2。 (
×
)(2) 平行四边形底与高的比是$5:4$,说明平行四边形的底是 5 分米,高是 4 分米。 (
×
)(3) 一个比的前项乘 0.5,后项除以 2,则比值不变。 (
√
)答案:2.
(1)×
(2)×
(3)√
(1)×
(2)×
(3)√
3. 化简下面各比。
$\frac {8}{9}:\frac {4}{15}$
$\frac {8}{9}:\frac {4}{15}$
10:3
$0.5m^{3}:120L$25:6
$\frac {1}{2}$时:20 分3:2
答案:3. 10:3 25:6 3:2
解析:
$\frac{8}{9}:\frac{4}{15}=\left(\frac{8}{9}×45\right):\left(\frac{4}{15}×45\right)=40:12=10:3$
$0.5\,\text{m}^3:120\,\text{L}=500\,\text{L}:120\,\text{L}=500:120=25:6$
$\frac{1}{2}$时:20分$=30$分:20分$=30:20=3:2$
$0.5\,\text{m}^3:120\,\text{L}=500\,\text{L}:120\,\text{L}=500:120=25:6$
$\frac{1}{2}$时:20分$=30$分:20分$=30:20=3:2$
4. 把下面各比改写成后项是 100 的比。
(1) 实验小学六年级男生人数与女生人数的比是$27:25$。 (
(2) 一批零件,合格的个数与零件总个数的比是$288:300$。 (
(1) 实验小学六年级男生人数与女生人数的比是$27:25$。 (
108:100
)(2) 一批零件,合格的个数与零件总个数的比是$288:300$。 (
96:100
)答案:4.
(1)108:100
(2)96:100
(1)108:100
(2)96:100
5.
| | 咖啡/克 | 水/克 | 咖啡与水质量的最简单的整数比 |
| 第1杯 | 5 | 120 |
| 第2杯 | 8 | 200 |
| 第(
| | 咖啡/克 | 水/克 | 咖啡与水质量的最简单的整数比 |
| 第1杯 | 5 | 120 |
1:24
|| 第2杯 | 8 | 200 |
1:25
|| 第(
1
)杯咖啡浓。 | | | |答案:5. 1:24 1:25 1
6. 看图答题。(结果保留 π,用最简单的整数比表示)
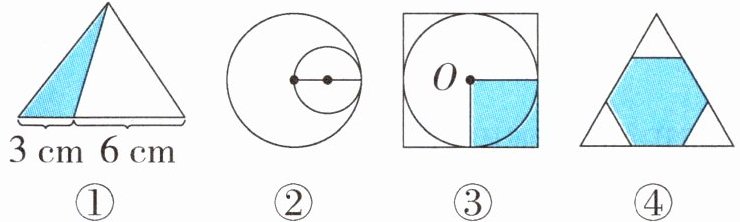
(1) 图①中,涂色部分与空白部分的面积比是(
(2) 图②中,大圆与小圆的直径比是(
(3) 图③中,圆与大正方形的周长比是(
(4) 图④中,大等边三角形内有一个正六边形,正六边形与大等边三角形的周长比是(

(1) 图①中,涂色部分与空白部分的面积比是(
1:2
)。(2) 图②中,大圆与小圆的直径比是(
2:1
),周长比是(2:1
),面积比是(4:1
)。(3) 图③中,圆与大正方形的周长比是(
π:4
),小正方形与圆的面积比是(1:π
)。(4) 图④中,大等边三角形内有一个正六边形,正六边形与大等边三角形的周长比是(
2:3
),面积比是(2:3
)。答案:6.
(1)1:2
(2)2:1 2:1 4:1
(3)π:4 1:π
(4)2:3 2:3
(1)1:2
(2)2:1 2:1 4:1
(3)π:4 1:π
(4)2:3 2:3
7. 如图是甲、乙、丙三人单独走完同一段路所需要的时间统计图。

(1) 甲、乙两人所用的时间比是$3:4$,乙单独走完这段路用了(
(2) 甲、丙两人的速度比是(

(1) 甲、乙两人所用的时间比是$3:4$,乙单独走完这段路用了(
16
)分。(2) 甲、丙两人的速度比是(
5:4
)。答案:7.
(1)16
(2)5:4
(1)16
(2)5:4
8. (1)$3:16= (3+6):(16+
$36:48= (36-
$45:60= (45÷15):(60-
(2)$a:b= 5:6,b:c= 2:1$,则$a:b:c= (
(3) 下面三幅图中,对应的面积比是$5:3$的有(

(4) 如图,涂色部分的面积占甲面积的$\frac {2}{5}$,占乙面积的$\frac {4}{7}$,则甲、乙的面积比是(

(5) 如图,大长方形被平均分成4份,甲的长与宽的比是$2:1$,乙的长与宽的比是(
32
)$$36:48= (36-
33
):(48-44)$$45:60= (45÷15):(60-
56
)$(2)$a:b= 5:6,b:c= 2:1$,则$a:b:c= (
5
):(6
):(3
)$。(3) 下面三幅图中,对应的面积比是$5:3$的有(
3
)个。(单位:厘米)
(4) 如图,涂色部分的面积占甲面积的$\frac {2}{5}$,占乙面积的$\frac {4}{7}$,则甲、乙的面积比是(
10:7
)。
(5) 如图,大长方形被平均分成4份,甲的长与宽的比是$2:1$,乙的长与宽的比是(
9:2
)。答案:8.
(1)32 33 56 提示:第一行:比的前项由3变为3+6=9,而3×3=9,根据比的基本性质,比的前项和后项同时乘或除以相同的数(0除外),比值不变,要使比值不变,比的后项也要乘3,即16×3=48,48-16=32,所以方框中填32。第二行:比的后项由48变成了48-44=4,而48÷4=12,根据比的基本性质,比的前项和后项同时乘或除以相同的数(0除外),比值不变,要使比值不变,比的前项也要除以12,即36÷12=3,36-3=33,所以方框中填33。第三行:比的前项由45变成了45÷15=3,根据比的基本性质,比的前项和后项同时乘或除以相同的数(0除外),比值不变,要使比值不变,比的后项也要除以15,即60÷15=4,60-4=56,所以方框中填56。
(2)5 6 3 提示:抓住中间量b,由于b在两个比中份数不一样,所以要统一b的份数,6和2的最小公倍数是6,b:c=2:1=6:3,所以a:b:c=5:6:3。
(3)3 提示:第1幅题图,$S_{甲}=(1+4)×高÷2$,$S_{乙}=3×高÷2$,所以$S_{甲}:S_{乙}=5:3$;第2幅题图,$S_{空白}=2×3÷2+3×4÷2+2×6÷2=15$(平方厘米),$S_{涂色}=4×6-15=9$(平方厘米),$S_{空白}:S_{涂色}=15:9=5:3$;第3幅题图,假设每个小长方形的宽为1,则$S_{整体}=5×高$,$S_{涂色}=(2+4)×高÷2=3×高$,$S_{整体}:S_{涂色}=5:3$,所以对应的面积比是5:3的有3个。
(4)10:7 提示:设涂色部分的面积是a,则甲的面积是$a÷\frac {2}{5}=\frac {5}{2}a$,乙的面积是$a÷\frac {4}{7}=\frac {7}{4}a$,甲、乙的面积比=$\frac {5}{2}a:\frac {7}{4}a=10:7$。
(5)9:2 提示:设甲的宽为1厘米,则它的长为2厘米,面积为2平方厘米。大长方形的面积为$2×4=8$(平方厘米),由于大长方形的宽就是甲的长,即2厘米,所以大长方形的长$=8÷2=4$(厘米),则乙的长$=4-1=3$(厘米),宽是$2÷3=\frac {2}{3}$(厘米),乙的长与宽的比是$3:\frac {2}{3}=9:2$。
(1)32 33 56 提示:第一行:比的前项由3变为3+6=9,而3×3=9,根据比的基本性质,比的前项和后项同时乘或除以相同的数(0除外),比值不变,要使比值不变,比的后项也要乘3,即16×3=48,48-16=32,所以方框中填32。第二行:比的后项由48变成了48-44=4,而48÷4=12,根据比的基本性质,比的前项和后项同时乘或除以相同的数(0除外),比值不变,要使比值不变,比的前项也要除以12,即36÷12=3,36-3=33,所以方框中填33。第三行:比的前项由45变成了45÷15=3,根据比的基本性质,比的前项和后项同时乘或除以相同的数(0除外),比值不变,要使比值不变,比的后项也要除以15,即60÷15=4,60-4=56,所以方框中填56。
(2)5 6 3 提示:抓住中间量b,由于b在两个比中份数不一样,所以要统一b的份数,6和2的最小公倍数是6,b:c=2:1=6:3,所以a:b:c=5:6:3。
(3)3 提示:第1幅题图,$S_{甲}=(1+4)×高÷2$,$S_{乙}=3×高÷2$,所以$S_{甲}:S_{乙}=5:3$;第2幅题图,$S_{空白}=2×3÷2+3×4÷2+2×6÷2=15$(平方厘米),$S_{涂色}=4×6-15=9$(平方厘米),$S_{空白}:S_{涂色}=15:9=5:3$;第3幅题图,假设每个小长方形的宽为1,则$S_{整体}=5×高$,$S_{涂色}=(2+4)×高÷2=3×高$,$S_{整体}:S_{涂色}=5:3$,所以对应的面积比是5:3的有3个。
(4)10:7 提示:设涂色部分的面积是a,则甲的面积是$a÷\frac {2}{5}=\frac {5}{2}a$,乙的面积是$a÷\frac {4}{7}=\frac {7}{4}a$,甲、乙的面积比=$\frac {5}{2}a:\frac {7}{4}a=10:7$。
(5)9:2 提示:设甲的宽为1厘米,则它的长为2厘米,面积为2平方厘米。大长方形的面积为$2×4=8$(平方厘米),由于大长方形的宽就是甲的长,即2厘米,所以大长方形的长$=8÷2=4$(厘米),则乙的长$=4-1=3$(厘米),宽是$2÷3=\frac {2}{3}$(厘米),乙的长与宽的比是$3:\frac {2}{3}=9:2$。