9. (1) 一列动车和一列特快列车分别从上海和南京同时出发,相向而行,在途中相遇。相遇点与中点的距离占全程的$\frac {1}{5}$,动车与特快列车所行路程的比是(
(2) 一项工程,如果分别由 A、B、C 三人单独完成,A 需要 12 天,B 需要的天数是 A 的$\frac {3}{4}$,C 需要的天数比 B 多 1 天,A、B、C 的工作效率比是(
(3) 用两根绳子测量同一口井的深度,第一根绳子有$\frac {1}{3}$露在井口外面,第二根绳子有$\frac {1}{5}$露在井口外面,那么第一根绳子与第二根绳子的长度比是(
7:3
)。(动车的速度快)(2) 一项工程,如果分别由 A、B、C 三人单独完成,A 需要 12 天,B 需要的天数是 A 的$\frac {3}{4}$,C 需要的天数比 B 多 1 天,A、B、C 的工作效率比是(
15:20:18
)。(3) 用两根绳子测量同一口井的深度,第一根绳子有$\frac {1}{3}$露在井口外面,第二根绳子有$\frac {1}{5}$露在井口外面,那么第一根绳子与第二根绳子的长度比是(
6:5
)。答案:9.
(1)7:3 提示:相遇时,动车所行的路程占全程的$\frac {1}{2}+\frac {1}{5}=\frac {7}{10}$,特快列车所行的路程占全程的$\frac {1}{2}-\frac {1}{5}=\frac {3}{10}$,由此可求出动车与特快列车所行路程的比是$\frac {7}{10}:\frac {3}{10}=7:3$。
(2)15:20:18 提示:将这项工程看作单位“1”。则A的工作效率是$\frac {1}{12}$;$12×\frac {3}{4}=9$(天),B的工作效率是$\frac {1}{9}$;$9+1=10$(天),C的工作效率是$\frac {1}{10}$,A、B、C的工作效率比是$\frac {1}{12}:\frac {1}{9}:\frac {1}{10}=15:20:18$。
(3)6:5 提示:根据“测量同一口井”可知“第一根绳子的$\frac {2}{3}=$第二根绳子的$\frac {4}{5}$”,所以第一根绳子可以用$\frac {3}{2}$表示,第二根绳子可以用$\frac {5}{4}$表示,第一根绳子与第二根绳子的长度比是$\frac {3}{2}:\frac {5}{4}=6:5$。
(1)7:3 提示:相遇时,动车所行的路程占全程的$\frac {1}{2}+\frac {1}{5}=\frac {7}{10}$,特快列车所行的路程占全程的$\frac {1}{2}-\frac {1}{5}=\frac {3}{10}$,由此可求出动车与特快列车所行路程的比是$\frac {7}{10}:\frac {3}{10}=7:3$。
(2)15:20:18 提示:将这项工程看作单位“1”。则A的工作效率是$\frac {1}{12}$;$12×\frac {3}{4}=9$(天),B的工作效率是$\frac {1}{9}$;$9+1=10$(天),C的工作效率是$\frac {1}{10}$,A、B、C的工作效率比是$\frac {1}{12}:\frac {1}{9}:\frac {1}{10}=15:20:18$。
(3)6:5 提示:根据“测量同一口井”可知“第一根绳子的$\frac {2}{3}=$第二根绳子的$\frac {4}{5}$”,所以第一根绳子可以用$\frac {3}{2}$表示,第二根绳子可以用$\frac {5}{4}$表示,第一根绳子与第二根绳子的长度比是$\frac {3}{2}:\frac {5}{4}=6:5$。
10. 甲、乙两人去上班,甲比乙多走$\frac {1}{5}$的路程,而乙比甲走的时间少$\frac {1}{11}$。甲、乙两人的速度比是多少?
答案:10.$(1+\frac {1}{5}):1=6:5$ $1:(1-\frac {1}{11})=11:10$ $(6÷11):(5÷10)=12:11$ 提示:根据“甲比乙多走$\frac {1}{5}$的路程”可知,甲与乙所行路程的比是$(1+\frac {1}{5}):1=6:5$;根据“乙比甲走的时间少$\frac {1}{11}$”可知,甲与乙所行时间的比是$1:(1-\frac {1}{11})=11:10$,所以甲、乙两人的速度比是$(6÷11):(5÷10)=\frac {6}{11}:\frac {1}{2}=12:11$。
解析:
设乙走的路程为单位“1”,则甲走的路程为$1 + \frac{1}{5} = \frac{6}{5}$,甲与乙的路程比为$\frac{6}{5}:1 = 6:5$。
设甲走的时间为单位“1”,则乙走的时间为$1 - \frac{1}{11} = \frac{10}{11}$,甲与乙的时间比为$1:\frac{10}{11} = 11:10$。
速度 = 路程÷时间,所以甲的速度为$6÷11 = \frac{6}{11}$,乙的速度为$5÷10 = \frac{1}{2}$。
甲、乙速度比为$\frac{6}{11}:\frac{1}{2} = (\frac{6}{11}×22):(\frac{1}{2}×22) = 12:11$。
答:甲、乙两人的速度比是$12:11$。
设甲走的时间为单位“1”,则乙走的时间为$1 - \frac{1}{11} = \frac{10}{11}$,甲与乙的时间比为$1:\frac{10}{11} = 11:10$。
速度 = 路程÷时间,所以甲的速度为$6÷11 = \frac{6}{11}$,乙的速度为$5÷10 = \frac{1}{2}$。
甲、乙速度比为$\frac{6}{11}:\frac{1}{2} = (\frac{6}{11}×22):(\frac{1}{2}×22) = 12:11$。
答:甲、乙两人的速度比是$12:11$。
11. 在一次数学练习中,六(1)班男生的平均成绩是 89 分,女生的平均成绩是 90.1 分。全班的平均成绩是 89.6 分,这个班男生和女生的人数比是多少?
答案:11.89.6-89=0.6(分) 90.1-89.6=0.5(分) 0.6×男生人数=0.5×女生人数,男生人数:女生人数=5:6 提示:男生的平均成绩比全班的平均成绩少89.6-89=0.6(分),女生的平均成绩比全班的平均成绩多90.1-89.6=0.5(分),所以0.6×男生人数=0.5×女生人数,男生人数:女生人数=5:6。
解析:
设男生人数为$x$,女生人数为$y$。
$89.6 - 89 = 0.6$(分)
$90.1 - 89.6 = 0.5$(分)
$0.6x = 0.5y$
$x:y = 0.5:0.6 = 5:6$
答:这个班男生和女生的人数比是$5:6$。
$89.6 - 89 = 0.6$(分)
$90.1 - 89.6 = 0.5$(分)
$0.6x = 0.5y$
$x:y = 0.5:0.6 = 5:6$
答:这个班男生和女生的人数比是$5:6$。
12. 甲、乙、丙、丁四人赛跑,甲的速度比乙快$\frac {2}{5}$,乙的速度比丁慢$\frac {2}{9}$,丙是第一名,谁是第三名?
答案:12.甲:乙=(2+5):5=7:5=49:35,乙:丁=(9-2):9=7:9=35:45,甲:乙:丁=49:35:45,49>45>35,且丙是第一名,所以丁是第三名。 提示:由题意可知,乙是中间量,要统一乙的份数。根据甲比乙快$\frac {2}{5}$,可知甲:乙=7:5=49:35。根据乙比丁慢$\frac {2}{9}$,可知乙:丁=7:9=35:45。那么甲:乙:丁=49:35:45。
解析:
甲:乙=(1+$\frac{2}{5}$):1=7:5=49:35,乙:丁=(1-$\frac{2}{9}$):1=7:9=35:45,甲:乙:丁=49:35:45,49>45>35,且丙是第一名,所以丁是第三名。
13. 如图,已知正方形的边长为 2 厘米,求涂色部分$S_{1}与涂色部分S_{2}$面积的最简单的整数比。
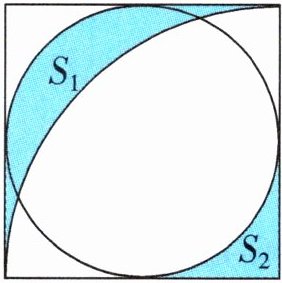

答案:13.直径为2厘米的整圆的面积:$π×(2÷2)^{2}=π$(平方厘米) 半径为2厘米的$\frac {1}{4}$圆的面积:$π×2^{2}÷4=π$(平方厘米) 因为$\frac {1}{4}$圆的面积+$S_{1}+S_{2}=$正方形的面积=整圆的面积+$4S_{2}$,所以正方形的面积-$\frac {1}{4}$圆的面积=$S_{1}+S_{2}$,正方形的面积-整圆的面积=$4S_{2}$,即$S_{1}+S_{2}=4S_{2}$,所以$S_{1}=3S_{2}$,所以$S_{1}:S_{2}=3:1$ 提示:题图中直径为2厘米的圆的面积为$π×(2÷2)^{2}=π$(平方厘米),半径为2厘米的$\frac {1}{4}$圆的面积为$π×2^{2}÷4=π$(平方厘米)。由于这两部分面积相等,所以用正方形的面积分别减去这两部分的面积,则剩下的面积相等,即$S_{1}+S_{2}=4S_{2}$,由此可得$S_{1}=3S_{2}$,故$S_{1}:S_{2}=3:1$。
解析:
直径为2厘米的整圆面积:$\pi×(2÷2)^2=\pi$(平方厘米)
半径为2厘米的$\frac{1}{4}$圆面积:$\pi×2^2÷4=\pi$(平方厘米)
正方形面积:$2×2 = 4$(平方厘米)
由图形关系得:正方形面积$-\frac{1}{4}$圆面积$=S_1 + S_2$,正方形面积$-$整圆面积$=4S_2$
即$4-\pi=S_1 + S_2$,$4-\pi=4S_2$
所以$S_1 + S_2=4S_2$,则$S_1=3S_2$
$S_1:S_2=3:1$
半径为2厘米的$\frac{1}{4}$圆面积:$\pi×2^2÷4=\pi$(平方厘米)
正方形面积:$2×2 = 4$(平方厘米)
由图形关系得:正方形面积$-\frac{1}{4}$圆面积$=S_1 + S_2$,正方形面积$-$整圆面积$=4S_2$
即$4-\pi=S_1 + S_2$,$4-\pi=4S_2$
所以$S_1 + S_2=4S_2$,则$S_1=3S_2$
$S_1:S_2=3:1$
14. 两个相同的瓶子装满酒精溶液,一个瓶中酒精与水的体积比是$3:1$,另一个瓶中酒精与水的体积比是$4:1$。若把这两瓶酒精溶液混合,求混合液中酒精与水的体积比。
答案:14.$(\frac {3}{1+3}+\frac {4}{1+4}):(\frac {1}{1+3}+\frac {1}{1+4})=31:9$ 提示:第一个瓶子中酒精的体积占酒精溶液体积的$\frac {3}{1+3}$,水的体积占酒精溶液体积的$\frac {1}{1+3}$;第二个瓶子中酒精的体积占酒精溶液体积的$\frac {4}{1+4}$,水的体积占酒精溶液体积的$\frac {1}{1+4}$。则混合液中酒精与水的体积比为$(\frac {3}{1+3}+\frac {4}{1+4}):(\frac {1}{1+3}+\frac {1}{1+4})$,然后化简比即可。
解析:
设每个瓶子的容积为单位“1”。
第一个瓶子中酒精体积为$\frac{3}{3+1} = \frac{3}{4}$,水体积为$\frac{1}{3+1} = \frac{1}{4}$;
第二个瓶子中酒精体积为$\frac{4}{4+1} = \frac{4}{5}$,水体积为$\frac{1}{4+1} = \frac{1}{5}$。
混合后酒精总体积为$\frac{3}{4} + \frac{4}{5} = \frac{15}{20} + \frac{16}{20} = \frac{31}{20}$,
水总体积为$\frac{1}{4} + \frac{1}{5} = \frac{5}{20} + \frac{4}{20} = \frac{9}{20}$。
混合液中酒精与水的体积比为$\frac{31}{20}:\frac{9}{20} = 31:9$。
第一个瓶子中酒精体积为$\frac{3}{3+1} = \frac{3}{4}$,水体积为$\frac{1}{3+1} = \frac{1}{4}$;
第二个瓶子中酒精体积为$\frac{4}{4+1} = \frac{4}{5}$,水体积为$\frac{1}{4+1} = \frac{1}{5}$。
混合后酒精总体积为$\frac{3}{4} + \frac{4}{5} = \frac{15}{20} + \frac{16}{20} = \frac{31}{20}$,
水总体积为$\frac{1}{4} + \frac{1}{5} = \frac{5}{20} + \frac{4}{20} = \frac{9}{20}$。
混合液中酒精与水的体积比为$\frac{31}{20}:\frac{9}{20} = 31:9$。