6. (1)把一根$\frac {9}{10}$米长的绳子平均剪成若干段,一共剪了 5 次,平均每段长(
(2)甲、乙两地相距 5600 米,小林和小轩同时从甲地到乙地去,小林和小轩的速度比是$4:3$,则小林到乙地时,小轩离乙地还有(
(3)大、小两个圆的周长比是$3:2$。若小圆的面积是 24 平方厘米,则大圆的面积是(
(4)一个平行四边形与一个三角形底的比是$1:2$,高的比是$1:2$。面积的比是(
$\frac{3}{20}$
)米。(2)甲、乙两地相距 5600 米,小林和小轩同时从甲地到乙地去,小林和小轩的速度比是$4:3$,则小林到乙地时,小轩离乙地还有(
1400
)米。(3)大、小两个圆的周长比是$3:2$。若小圆的面积是 24 平方厘米,则大圆的面积是(
54
)平方厘米;若大圆比小圆的面积多 25 平方厘米,则小圆的面积是(20
)平方厘米。(4)一个平行四边形与一个三角形底的比是$1:2$,高的比是$1:2$。面积的比是(
1:2
)。答案:6.
(1)$\frac{3}{20}$
(2)1400
(3)54 20
(4)1:2
(1)$\frac{3}{20}$
(2)1400
(3)54 20
(4)1:2
7. 运输队 3 天运走一批货物,第一天运走了60 吨,占这批货物的$\frac {2}{5}$,第二天和第三天运走的吨数比是$3:2$,第三天运走了多少吨?
答案:7.$60÷\frac{2}{5}=150$(吨) $150 - 60 = 90$(吨)
$90×\frac{2}{3 + 2}=36$(吨)
$90×\frac{2}{3 + 2}=36$(吨)
8. (1)从 2、4、6、8、10 这五个数中选择 4 个数填入算式,使商最大:$\frac {
(2)如果$a÷\frac {3}{10}= b÷\frac {5}{6}= c÷\frac {8}{7}$(a、b、c 均大于 0),比一比:$a÷\frac {b}{c}$
(3)科学课上乐老师展示“线灰悬针”的魔术,为此他要准备一瓶高浓度盐水。现在有一瓶重 120 克的盐水,盐与水的质量比是$1:5$,再加入
(4)甲、乙、丙三人合乘一辆出租车,讲好大家分摊车费,甲在全行程的$\frac {1}{3}$处下车,到了$\frac {2}{3}$处乙也下车了,最后丙一个人坐到终点,付给司机 60 元。则甲应付给丙
10
}{2
}÷\frac {4
}{8
}$。(2)如果$a÷\frac {3}{10}= b÷\frac {5}{6}= c÷\frac {8}{7}$(a、b、c 均大于 0),比一比:$a÷\frac {b}{c}$
>
a。(3)科学课上乐老师展示“线灰悬针”的魔术,为此他要准备一瓶高浓度盐水。现在有一瓶重 120 克的盐水,盐与水的质量比是$1:5$,再加入
15
克盐,就能配制成盐与水的质量比是$7:20$的实验用盐水。(4)甲、乙、丙三人合乘一辆出租车,讲好大家分摊车费,甲在全行程的$\frac {1}{3}$处下车,到了$\frac {2}{3}$处乙也下车了,最后丙一个人坐到终点,付给司机 60 元。则甲应付给丙
10
元,乙应付给丙20
元。答案:8.
(1)$\frac{10}{2}÷\frac{4}{8}$(答案不唯一) 提示:要使商最大,则被除数可以为$\frac{10}{2}$,除数可以为$\frac{4}{8}$,算式为$\frac{10}{2}÷\frac{4}{8}$。
(2)> 提示:假设$a÷\frac{3}{10}=b÷\frac{5}{6}=c÷\frac{8}{7}=1$,则$a = \frac{3}{10}$,$b = \frac{5}{6}$,$c = \frac{8}{7}$,即$a < b < c$,所以$\frac{b}{c} < 1$,则$a÷\frac{b}{c} > a$。
(3)15 提示:先求出盐水中原来有水$120÷(1 + 5)×5 = 100$(克),加入盐后,则配成的盐水共$100÷20×(20 + 7)=135$(克),即在原来的120克盐水中加了$135 - 120 = 15$(克)盐。
(4)10 20 提示:根据题意知,甲、乙、丙所乘坐的路程比为1:2:3,所以所分摊的车费比也应该是1:2:3,甲应付给丙$60×\frac{1}{1 + 2 + 3}=10$(元),乙应付给丙$10×2 = 20$(元)。
(1)$\frac{10}{2}÷\frac{4}{8}$(答案不唯一) 提示:要使商最大,则被除数可以为$\frac{10}{2}$,除数可以为$\frac{4}{8}$,算式为$\frac{10}{2}÷\frac{4}{8}$。
(2)> 提示:假设$a÷\frac{3}{10}=b÷\frac{5}{6}=c÷\frac{8}{7}=1$,则$a = \frac{3}{10}$,$b = \frac{5}{6}$,$c = \frac{8}{7}$,即$a < b < c$,所以$\frac{b}{c} < 1$,则$a÷\frac{b}{c} > a$。
(3)15 提示:先求出盐水中原来有水$120÷(1 + 5)×5 = 100$(克),加入盐后,则配成的盐水共$100÷20×(20 + 7)=135$(克),即在原来的120克盐水中加了$135 - 120 = 15$(克)盐。
(4)10 20 提示:根据题意知,甲、乙、丙所乘坐的路程比为1:2:3,所以所分摊的车费比也应该是1:2:3,甲应付给丙$60×\frac{1}{1 + 2 + 3}=10$(元),乙应付给丙$10×2 = 20$(元)。
9. 张达、朱诚、胡宁三名同学共有图书 198 本,张达比朱诚多 18 本,朱诚与胡宁的图书本数的比是$2:5$。张达有多少本图书?
答案:9.$198 - 18 = 180$(本) $180×\frac{2}{2 + 2 + 5}=40$(本)
$40 + 18 = 58$(本) 提示:若张达减少18本,则与朱诚的图书本数同样多,三人总本数则变成$198 - 18 = 180$(本),再根据三人的图书本数的比计算即可。
$40 + 18 = 58$(本) 提示:若张达减少18本,则与朱诚的图书本数同样多,三人总本数则变成$198 - 18 = 180$(本),再根据三人的图书本数的比计算即可。
10. 一辆客车和一辆货车同时从甲地开往乙地。2 小时后,客车距乙地还有全程的$\frac {1}{7}$,货车距乙地还有 55 千米。已知货车每小时比客车少行 15 千米,求甲、乙两地之间的路程。(先在下图中表示出相应的条件,再解答)
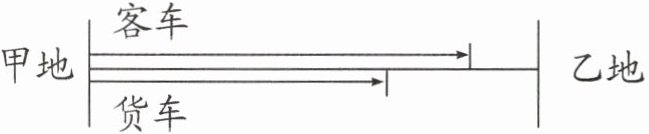

答案:
10.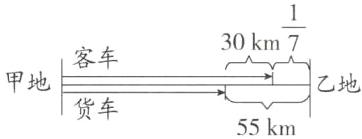
$55 - 15×2 = 25$(千米) $25÷\frac{1}{7}=175$(千米)
提示:根据题意可知,行了2小时后,客车与货车相距$15×2 = 30$(千米),$(55 - 30)$千米占全程的$\frac{1}{7}$,由此可求出甲、乙两地之间的路程。
10.

$55 - 15×2 = 25$(千米) $25÷\frac{1}{7}=175$(千米)
提示:根据题意可知,行了2小时后,客车与货车相距$15×2 = 30$(千米),$(55 - 30)$千米占全程的$\frac{1}{7}$,由此可求出甲、乙两地之间的路程。
11. 如图,直角三角形 ABC 的三条边的长分别是6 米、8 米、10 米,将它的最短边 AB 对折到最长边,与 AE 重合。求三角形 CDE 的面积。


答案:11.AB、AE和CE的长度比是6:6:(10 - 6)=3:3:2,则三角形ADB、三角形ADE和三角形CDE 的面积比是3:3:2
三角形ABC的面积为$6×8÷2 = 24$(平方米)
三角形CDE的面积为$24×\frac{2}{3 + 3 + 2}=6$(平方米)
提示:根据题意可知,三角形ADB与三角形ADE 完全相同,则AE的长是6米,CE的长是$10 - 6 = 4$(米)。三角形ADE与三角形CDE的高相等,底边的长度比是6:4 = 3:2,这两个三角形的面积比也是3:2。由于三角形ADB的面积与三角形ADE的面积相等,则三角形ADB、三角形ADE 与三角形CDE的面积比为3:3:2,把三角形ABC的面积按3:3:2的比进行分配,就可以求出三角形CDE的面积。
三角形ABC的面积为$6×8÷2 = 24$(平方米)
三角形CDE的面积为$24×\frac{2}{3 + 3 + 2}=6$(平方米)
提示:根据题意可知,三角形ADB与三角形ADE 完全相同,则AE的长是6米,CE的长是$10 - 6 = 4$(米)。三角形ADE与三角形CDE的高相等,底边的长度比是6:4 = 3:2,这两个三角形的面积比也是3:2。由于三角形ADB的面积与三角形ADE的面积相等,则三角形ADB、三角形ADE 与三角形CDE的面积比为3:3:2,把三角形ABC的面积按3:3:2的比进行分配,就可以求出三角形CDE的面积。
12. 如图,一个长方形被分割成 5 个正方形。已知每个大正方形的面积比每个小正方形的面积大 15 平方厘米,求一个大正方形的面积。


答案:12.$1.5:1 = 3:2$ $3^{2}:2^{2}=9:4$
$15×\frac{9}{9 - 4}=27$(平方厘米) 提示:从题图中可以看出,大正方形的边长是小正方形边长的1.5倍,则大正方形与小正方形的边长比是$1.5:1 = 3:2$,面积比是$3^{2}:2^{2}=9:4$。一个大正方形的面积占大、小正方形面积差的$\frac{9}{9 - 4}$,则一个大正方形的面积为$15×\frac{9}{9 - 4}=27$(平方厘米)。
$15×\frac{9}{9 - 4}=27$(平方厘米) 提示:从题图中可以看出,大正方形的边长是小正方形边长的1.5倍,则大正方形与小正方形的边长比是$1.5:1 = 3:2$,面积比是$3^{2}:2^{2}=9:4$。一个大正方形的面积占大、小正方形面积差的$\frac{9}{9 - 4}$,则一个大正方形的面积为$15×\frac{9}{9 - 4}=27$(平方厘米)。