$\frac{6}{13}÷\frac{3}{13}= (6×\frac{1}{13})÷(
$\frac{b}{a}÷\frac{d}{c}=
3
×\frac{1}{13}
)=6÷3=2
$$\frac{b}{a}÷\frac{d}{c}=
(bc×\frac{1}{ac})÷(ad×\frac{1}{ac})=(bc)÷(ad)=\frac{bc}{ad}
$答案:3 $\frac{1}{13}$ $6÷3=2$ $(bc×\frac{1}{ac})÷(ad×\frac{1}{ac})=(bc)÷(ad)=\frac{bc}{ad}$ 提示:把被除数和除数分别写成整数乘相同计数单位的形式,再根据商的变化规律将相同的计数单位消去,就可以将原来的运算转化为计数单位个数相除的运算。
解析:
3 $\frac{1}{13}$ $6÷3=2$ $(b×\frac{1}{a})÷(d×\frac{1}{c})=(b× c)÷(d× a)=\frac{bc}{ad}$
6. 推导探究 (1) 判断这道题的计算结果是否正确:$\frac{8}{15}÷\frac{2}{3}= \frac{8÷2}{15÷3}= \frac{4}{5}$。(
(2) 如果你认真思考,仔细观察,会有新的发现。
假设:$a$、$b$、$c$、$d$均为非 0 自然数。
$\frac{b}{a}÷\frac{d}{c}= \frac{b}{a}×\frac{c}{d}= \frac{bc}{ad}$,$\frac{b÷d}{a÷c}= \frac{b}{d}÷\frac{c}{a}= \frac{b}{d}×\frac{c}{a}= \frac{bc}{ad}$,则$\frac{b}{a}÷\frac{d}{c}= \frac{b÷d}{a÷c}$。
看来,分数除以分数,还有另一种计算方法:分数除以分数,用被除数的(
$\frac{4}{27}÷\frac{2}{9}=$
$\frac{28}{45}÷\frac{7}{5}=$
正确
)(2) 如果你认真思考,仔细观察,会有新的发现。
假设:$a$、$b$、$c$、$d$均为非 0 自然数。
$\frac{b}{a}÷\frac{d}{c}= \frac{b}{a}×\frac{c}{d}= \frac{bc}{ad}$,$\frac{b÷d}{a÷c}= \frac{b}{d}÷\frac{c}{a}= \frac{b}{d}×\frac{c}{a}= \frac{bc}{ad}$,则$\frac{b}{a}÷\frac{d}{c}= \frac{b÷d}{a÷c}$。
看来,分数除以分数,还有另一种计算方法:分数除以分数,用被除数的(
分子
)除以除数的(分子
)作分子,被除数的(分母
)除以除数的(分母
)作分母。特别是当被除数的分子、分母分别是除数的分子、分母的倍数时,用这种方法尤为快捷和简便。请你用下题进行验证。$\frac{4}{27}÷\frac{2}{9}=$
$\frac{4÷2}{27÷9}=\frac{2}{3}$
$\frac{28}{45}÷\frac{7}{5}=$
$\frac{28÷7}{45÷5}=\frac{4}{9}$
答案:
(1)正确 提示:根据分数除法的计算方法算出$\frac {8}{15}÷\frac {2}{3}=\frac {8}{15}×\frac {3}{2}=\frac {4}{5}$,可以判断计算结果正确。
(2)分子 分子 分母 分母 $\frac {4}{27}÷\frac {2}{9}=\frac {4÷2}{27÷9}=\frac {2}{3}$ $\frac {28}{45}÷\frac {7}{5}=\frac {28÷7}{45÷5}=\frac {4}{9}$ 提示:根据发现的计算方法计算即可。
(1)正确 提示:根据分数除法的计算方法算出$\frac {8}{15}÷\frac {2}{3}=\frac {8}{15}×\frac {3}{2}=\frac {4}{5}$,可以判断计算结果正确。
(2)分子 分子 分母 分母 $\frac {4}{27}÷\frac {2}{9}=\frac {4÷2}{27÷9}=\frac {2}{3}$ $\frac {28}{45}÷\frac {7}{5}=\frac {28÷7}{45÷5}=\frac {4}{9}$ 提示:根据发现的计算方法计算即可。
7. (1) 数感 算式$\frac{2}{7}÷\frac{2}{3}×\frac{5}{3}÷\frac{6}{7}×\frac{1}{2}= \frac{3}{20}$有一个运算符号写错了,把它改成正确的算式是 。
(2) 几何直观 如图,沿一个正方形的对角线将其分为两个等腰直角三角形,$M$、$N$是两个正方形。$M$、$N$的面积之比是( )。
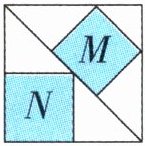
(2) 几何直观 如图,沿一个正方形的对角线将其分为两个等腰直角三角形,$M$、$N$是两个正方形。$M$、$N$的面积之比是( )。

答案:
(1)$\frac {2}{7}÷\frac {2}{3}÷\frac {5}{3}÷\frac {6}{7}×\frac {1}{2}=\frac {3}{20}$ 提示:因为算式得数的分母20含有因数5,且只有一个运算符号写错了,可以猜测$\frac {5}{3}$前面的"×"错了,把"×"改成"÷",再验证即可。
(2)$8:9$ 提示:如图分割,M中每个小三角形与N中每个小三角形面积的比是$8:9$,所以M、N的面积比也是$8:9$。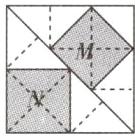
(1)$\frac {2}{7}÷\frac {2}{3}÷\frac {5}{3}÷\frac {6}{7}×\frac {1}{2}=\frac {3}{20}$ 提示:因为算式得数的分母20含有因数5,且只有一个运算符号写错了,可以猜测$\frac {5}{3}$前面的"×"错了,把"×"改成"÷",再验证即可。
(2)$8:9$ 提示:如图分割,M中每个小三角形与N中每个小三角形面积的比是$8:9$,所以M、N的面积比也是$8:9$。

8. 推理意识 一组割草人要把两片草地的草割掉。大的一片草地面积是小的一片草地的 2 倍。上午大家在大片草地上工作,午后分成两组,一半人继续在大片草地上割草,到傍晚收工时恰好割完;另一半人到小片草地上割草,到傍晚还剩一小块,这一小块第二天由一个人去割,恰好需要一天时间。请你算一下,这组割草人共有多少人?
答案:$\frac {1}{2}-\frac {1}{3}=\frac {1}{6}$ $1+\frac {1}{3}=\frac {4}{3}$ $\frac {4}{3}÷\frac {1}{6}=8$(人) 提示:因为大的一片草地需全组割草人割半天以后,还需一半割草人再割半天,那么很显然,一半割草人半天时间可割这块地的$\frac {1}{3}$,因此小片草地上留下的没割的一块是大片草地的$\frac {1}{2}-\frac {1}{3}=\frac {1}{6}$。这样,一个割草人每天能割大片草地的$\frac {1}{6}$,而当天割草一共是割了大片草地的$1+\frac {1}{3}=\frac {4}{3}$,所以割草人共$\frac {4}{3}÷\frac {1}{6}=8$(人)。
解析:
设大片草地面积为单位"1",则小片草地面积为$\frac{1}{2}$。
全组人上午在大片草地割草,下午一半人继续割,恰好割完。全组人半天的工作量加一半人半天的工作量等于大片草地面积,即全组人半天工作量为$\frac{2}{3}$,一半人半天工作量为$\frac{1}{3}$。
另一半人在小片草地割草半天,完成工作量为$\frac{1}{3}$,剩余工作量为$\frac{1}{2}-\frac{1}{3}=\frac{1}{6}$,此工作量需1人1天完成,即1人1天割草$\frac{1}{6}$。
当天全组割草总量为大片草地1加小片草地已割的$\frac{1}{3}$,即$1+\frac{1}{3}=\frac{4}{3}$。
割草人数为$\frac{4}{3}÷\frac{1}{6}=8$人。
8
全组人上午在大片草地割草,下午一半人继续割,恰好割完。全组人半天的工作量加一半人半天的工作量等于大片草地面积,即全组人半天工作量为$\frac{2}{3}$,一半人半天工作量为$\frac{1}{3}$。
另一半人在小片草地割草半天,完成工作量为$\frac{1}{3}$,剩余工作量为$\frac{1}{2}-\frac{1}{3}=\frac{1}{6}$,此工作量需1人1天完成,即1人1天割草$\frac{1}{6}$。
当天全组割草总量为大片草地1加小片草地已割的$\frac{1}{3}$,即$1+\frac{1}{3}=\frac{4}{3}$。
割草人数为$\frac{4}{3}÷\frac{1}{6}=8$人。
8
9. 一个密闭的长方体容器里装着一些水,如果把它的上面、前面、右面分别平放在地面上的时候,水面的高度分别为 4 厘米、6 厘米、10 厘米。那么这个长方体容器的长、宽、高的比是多少?
答案:$10:6:4=5:3:2$ 提示:设长方体容器的长、宽、高分别为a、b、c,水的体积为V。把它的上面平放,底面积就是长乘宽;把它的前面平放,底面积就是长乘高;把它的右面平放,底面积就是宽乘高。无论是上面平放在地上、前面平放在地上还是右面平放在地上,水的体积保持不变。$V = 4ab = 6ac = 10bc$,所以$6a = 10b,a:b = 10:6,4b = 6c,b:c = 6:4$,即$a:b:c = 10:6:4 = 5:3:2$。这个长方体容器的长、宽、高的比是$5:3:2$。
解析:
设长方体容器的长、宽、高分别为$a$、$b$、$c$,水的体积为$V$。
因为水的体积不变,所以:
当上面平放在地面时,$V = 4ab$;
当前面平放在地面时,$V = 6ac$;
当右面平放在地面时,$V = 10bc$。
由$4ab = 6ac$,两边同时除以$2a$($a \neq 0$),得$2b = 3c$,即$b:c = 3:2$;
由$4ab = 10bc$,两边同时除以$2b$($b \neq 0$),得$2a = 5c$,即$a:c = 5:2$。
所以$a:b:c = 5:3:2$。
这个长方体容器的长、宽、高的比是$5:3:2$。
因为水的体积不变,所以:
当上面平放在地面时,$V = 4ab$;
当前面平放在地面时,$V = 6ac$;
当右面平放在地面时,$V = 10bc$。
由$4ab = 6ac$,两边同时除以$2a$($a \neq 0$),得$2b = 3c$,即$b:c = 3:2$;
由$4ab = 10bc$,两边同时除以$2b$($b \neq 0$),得$2a = 5c$,即$a:c = 5:2$。
所以$a:b:c = 5:3:2$。
这个长方体容器的长、宽、高的比是$5:3:2$。