例1 甲数是乙数的$\frac {3}{10}$,乙数是丙数的$\frac {4}{5}$,甲、乙、丙三个数均不为0,求甲、乙、丙三个数的比。
分析:方法一:借助中间量法。可以先找出乙数在两个比中的两个份数的最小公倍数,再利用比的基本性质,使其相等后,写出三个数的比。
甲数是乙数的$\frac {3}{10}$→甲:乙$=3:10= 6:20$;
乙数是丙数的$\frac {4}{5}$→乙:丙$=4:5= 20:25$。
所以甲:乙:丙$=6:20:25$。
方法二:设数法。可以设乙数为10,再分别求出甲、丙两数。
甲$=10×\frac {3}{10}= 3$,丙$=10÷\frac {4}{5}= \frac {25}{2}$。
所以甲:乙:丙$=3:10:\frac {25}{2}= 6:20:25$。
解决此类题的关键是将几个比中的同一个量转化成相同的数,从而可以得到几个数的连比。
解答:甲:乙:丙$=6:20:25$
分析:方法一:借助中间量法。可以先找出乙数在两个比中的两个份数的最小公倍数,再利用比的基本性质,使其相等后,写出三个数的比。
甲数是乙数的$\frac {3}{10}$→甲:乙$=3:10= 6:20$;
乙数是丙数的$\frac {4}{5}$→乙:丙$=4:5= 20:25$。
所以甲:乙:丙$=6:20:25$。
方法二:设数法。可以设乙数为10,再分别求出甲、丙两数。
甲$=10×\frac {3}{10}= 3$,丙$=10÷\frac {4}{5}= \frac {25}{2}$。
所以甲:乙:丙$=3:10:\frac {25}{2}= 6:20:25$。
解决此类题的关键是将几个比中的同一个量转化成相同的数,从而可以得到几个数的连比。
解答:甲:乙:丙$=6:20:25$
答案:解析:本题考查的是比的基本性质和比的计算。
可以用设数法,设乙数为$10$。
甲数是乙数的$\frac{3}{10}$,所以甲数为:
$10 × \frac{3}{10} = 3$,
乙数是丙数的$\frac{4}{5}$,所以丙数为:
$10 ÷ \frac{4}{5} = \frac{25}{2}$,
所以甲数:乙数:丙数 = $3:10:\frac{25}{2} = 6:20:25$。
答案:甲:乙:丙$= 6:20:25$。
可以用设数法,设乙数为$10$。
甲数是乙数的$\frac{3}{10}$,所以甲数为:
$10 × \frac{3}{10} = 3$,
乙数是丙数的$\frac{4}{5}$,所以丙数为:
$10 ÷ \frac{4}{5} = \frac{25}{2}$,
所以甲数:乙数:丙数 = $3:10:\frac{25}{2} = 6:20:25$。
答案:甲:乙:丙$= 6:20:25$。
1. 张大爷家养的鸡与鸭的只数比是$7:2$,养的鸭的只数是鹅的$\frac {3}{4}$,张大爷家养的鸡、鸭、鹅的只数比是
21:6:8
。答案:21:6:8 提示:因为鸡与鸭的只数比为7:2,两边同时乘3,假设鸡有21只,则鸭有6只,是鹅的$\frac{3}{4}$,则鹅有$6÷\frac{3}{4}=8$(只),因此鸡、鸭、鹅的只数比是21:6:8。
解析:
鸡与鸭的只数比为$7:2$,两边同时乘3,得鸡$:$鸭$=21:6$。
鸭的只数是鹅的$\frac{3}{4}$,设鹅的只数为$x$,则$6=\frac{3}{4}x$,解得$x=6÷\frac{3}{4}=8$,即鸭$:$鹅$=6:8$。
所以鸡、鸭、鹅的只数比是$21:6:8$。
$21:6:8$
鸭的只数是鹅的$\frac{3}{4}$,设鹅的只数为$x$,则$6=\frac{3}{4}x$,解得$x=6÷\frac{3}{4}=8$,即鸭$:$鹅$=6:8$。
所以鸡、鸭、鹅的只数比是$21:6:8$。
$21:6:8$
2. 如图,下面三个图形的周长相等,则$a:b:c=$
20
:25
:24
。答案:20 25 24 提示:三个图形的周长分别是6a、4b+a、5c,且它们的周长相等,可得出4b+a=6a,即4b=5a,得出$b=\frac{5}{4}a$,同理$c=\frac{6}{5}a$。所以a:b:c=$a:\frac{5}{4}a:\frac{6}{5}a$=20:25:24。
解析:
三个图形的周长分别是$2×(2a+a)=6a$、$2b+2b+a=4b+a$、$5c$。
因为周长相等,所以$4b+a=6a$,即$4b=5a$,得$b=\frac{5}{4}a$;
同理$5c=6a$,得$c=\frac{6}{5}a$。
则$a:b:c=a:\frac{5}{4}a:\frac{6}{5}a$,通分后为$20:25:24$。
20 25 24
因为周长相等,所以$4b+a=6a$,即$4b=5a$,得$b=\frac{5}{4}a$;
同理$5c=6a$,得$c=\frac{6}{5}a$。
则$a:b:c=a:\frac{5}{4}a:\frac{6}{5}a$,通分后为$20:25:24$。
20 25 24
例2 甲、乙、丙三个仓库共存粮85吨,甲仓库比乙仓库多存粮1吨,丙仓库与乙仓库存粮吨数的比是$3:2$,甲仓库存粮多少吨?
分析:假设甲仓库与乙仓库存粮吨数相等,则三个仓库共存粮$85-1= 84$(吨),且甲、乙、丙三个仓库存粮吨数的比应为$2:2:3$,再用按比例分配的方法求出乙仓库存粮的吨数,最后用乙仓库存粮吨数加上1便可求出甲仓库存粮的吨数。
解答:$85-1= 84$(吨)$84×\frac {2}{2+2+3}= 24$(吨)
$24+1= 25$(吨)
分析:假设甲仓库与乙仓库存粮吨数相等,则三个仓库共存粮$85-1= 84$(吨),且甲、乙、丙三个仓库存粮吨数的比应为$2:2:3$,再用按比例分配的方法求出乙仓库存粮的吨数,最后用乙仓库存粮吨数加上1便可求出甲仓库存粮的吨数。
解答:$85-1= 84$(吨)$84×\frac {2}{2+2+3}= 24$(吨)
$24+1= 25$(吨)
答案:分析:
本题考查的是比例的应用。
假设甲仓库与乙仓库存粮吨数相等,则三个仓库共存粮$85 - 1 = 84$(吨),
且甲、乙、丙三个仓库存粮吨数的比应为$2:2:3$。
再用按比例分配的方法求出乙仓库存粮的吨数,
最后用乙仓库存粮吨数加上$1$便可求出甲仓库存粮的吨数。
解答:
$85 - 1 = 84$(吨)
乙仓库存粮的吨数为:
$84 × \frac{2}{2+2+3} = 24$(吨)
甲仓库存粮的吨数为:
$24 + 1 = 25$(吨)
所以,甲仓库存粮为$25$吨。
本题考查的是比例的应用。
假设甲仓库与乙仓库存粮吨数相等,则三个仓库共存粮$85 - 1 = 84$(吨),
且甲、乙、丙三个仓库存粮吨数的比应为$2:2:3$。
再用按比例分配的方法求出乙仓库存粮的吨数,
最后用乙仓库存粮吨数加上$1$便可求出甲仓库存粮的吨数。
解答:
$85 - 1 = 84$(吨)
乙仓库存粮的吨数为:
$84 × \frac{2}{2+2+3} = 24$(吨)
甲仓库存粮的吨数为:
$24 + 1 = 25$(吨)
所以,甲仓库存粮为$25$吨。
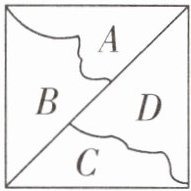
3. 如图,这个正方形被分成了4个部分。其中,A和B的面积比是$2:3$,B和C的面积比是$2:1$。如果D的面积是35平方厘米,那么正方形的面积是(
100
)平方厘米。
答案:100 提示:从两个比中可以看出,B的面积是中间量,可以把表示B的面积的份数转化为相同的份数,即2:3=4:6,2:1=6:3,所以A:B:C=4:6:3。由于A与B的面积和等于C与D的面积和,所以D的面积有4+6-3=7(份),正方形的面积有(4+6)×2=20(份)。正方形的面积=$35÷\frac{7}{20}=100$(平方厘米)。
解析:
A:B=2:3=4:6,B:C=2:1=6:3,所以A:B:C=4:6:3。
因为A+B=C+D,所以D的份数为4+6-3=7份。
正方形面积份数为(4+6)×2=20份。
每份面积为35÷7=5平方厘米。
正方形面积为20×5=100平方厘米。
100
因为A+B=C+D,所以D的份数为4+6-3=7份。
正方形面积份数为(4+6)×2=20份。
每份面积为35÷7=5平方厘米。
正方形面积为20×5=100平方厘米。
100
4. 甲、乙、丙三个仓库共存粮2100吨,甲仓库运出270吨,乙仓库运进150吨,丙仓库运出自己存粮吨数的$\frac {1}{3}$,这时三个仓库存粮吨数的比是$5:3:2$,原来三个仓库各存粮多少吨?
答案:2100-270+150=1980(吨)甲仓库:$1980×\frac{5}{5+3+3}+270=1170$(吨)丙仓库:$1980×\frac{3}{5+3+3}=540$(吨)乙仓库:$540-150=390$(吨) 提示:假设丙仓库不运出粮食,现在甲、乙、丙三个仓库共存粮2100-270+150=1980(吨),它们的存粮吨数的比是5:3:3。把1980吨按5:3:3进行分配可求出丙仓库原来的存粮吨数,以及甲、乙两个仓库现在的存粮吨数,最后再求甲、乙两个仓库原来的存粮吨数。
解析:
2100-270+150=1980(吨)
丙仓库:$1980×\frac{3}{5+3+3}=540$(吨)
甲仓库现在:$1980×\frac{5}{5+3+3}=900$(吨)
甲仓库原来:$900+270=1170$(吨)
乙仓库现在:$1980×\frac{3}{5+3+3}=540$(吨)
乙仓库原来:$540-150=390$(吨)
答:原来甲仓库存粮1170吨,乙仓库存粮390吨,丙仓库存粮540吨。
丙仓库:$1980×\frac{3}{5+3+3}=540$(吨)
甲仓库现在:$1980×\frac{5}{5+3+3}=900$(吨)
甲仓库原来:$900+270=1170$(吨)
乙仓库现在:$1980×\frac{3}{5+3+3}=540$(吨)
乙仓库原来:$540-150=390$(吨)
答:原来甲仓库存粮1170吨,乙仓库存粮390吨,丙仓库存粮540吨。
5. 甲、乙两个修路队原有石子的质量比是$3:4$,乙队运了108吨给甲队,现在甲、乙两队的石子的质量比是$5:2$。原来甲、乙两队各有石子多少吨?
答案:$\frac{5}{5+2}-\frac{3}{3+4}=\frac{2}{7}$ 总质量:$108÷\frac{2}{7}=378$(吨)甲队:$378×\frac{3}{3+4}=162$(吨)乙队:$378×\frac{4}{3+4}=216$(吨) 提示:石子的总质量不变,原来甲队的石子的质量占石子总质量的$\frac{3}{3+4}=\frac{3}{7}$,后来甲队的石子的质量占石子总质量的$\frac{5}{5+2}=\frac{5}{7}$,$\frac{5}{7}-\frac{3}{7}=\frac{2}{7}$,石子的总质量为$108÷\frac{2}{7}=378$(吨),按原来的比例分配,甲队:$378×\frac{3}{3+4}=162$(吨),乙队:$378×\frac{4}{3+4}=216$(吨)。
解析:
石子总质量不变,原来甲队石子占总质量的比例为$\frac{3}{3 + 4} = \frac{3}{7}$,现在甲队石子占总质量的比例为$\frac{5}{5 + 2} = \frac{5}{5 + 2} = \frac{5}{7}$。甲队石子占总质量的比例增加了$\frac{5}{7} - \frac{3}{7} = \frac{2}{7}$。
因为乙队运了108吨给甲队,所以这108吨占总质量的$\frac{2}{7}$,则石子总质量为$108÷\frac{2}{7} = 108×\frac{7}{2} = 378$吨。
原来甲队有石子$378×\frac{3}{3 + 4} = 378×\frac{3}{7} = 162$吨,乙队有石子$378×\frac{4}{3 + 4} = 378×\frac{4}{7} = 216$吨。
答:原来甲队有石子162吨,乙队有石子216吨。
因为乙队运了108吨给甲队,所以这108吨占总质量的$\frac{2}{7}$,则石子总质量为$108÷\frac{2}{7} = 108×\frac{7}{2} = 378$吨。
原来甲队有石子$378×\frac{3}{3 + 4} = 378×\frac{3}{7} = 162$吨,乙队有石子$378×\frac{4}{3 + 4} = 378×\frac{4}{7} = 216$吨。
答:原来甲队有石子162吨,乙队有石子216吨。