1. $\frac {5}{8}= \frac {
25
}{40}= 40:64
= \frac {5+10}{8+16
}$答案:25 64 16
解析:
25;64;16
2. (
$\frac{3}{10}$
)千米是$\frac {9}{10}千米的\frac {1}{3}$,90吨是(225
)吨的$\frac {2}{5}$,$\frac {3}{4}公顷的\frac {(5
)}{(9
)}$等于$\frac {1}{2}公顷的\frac {5}{6}$。答案:$\frac{3}{10}$ 225 $\frac{5}{9}$
3. 在圆圈里填上“>”“<”或“=”。
$\frac {6}{7}÷\frac {3}{2}$
$\frac {3}{5}÷\frac {99}{100}$
$\frac {6}{7}÷\frac {3}{2}$
<
$\frac {6}{7}$ $\frac {7}{8}×\frac {10}{11}$=
$\frac {10}{11}÷\frac {8}{7}$$\frac {3}{5}÷\frac {99}{100}$
>
$\frac {3}{5}$ $\frac {5}{9}÷\frac {3}{5}$=
$\frac {5}{9}÷3×5$答案:< = > =
解析:
$\frac{6}{7}÷\frac{3}{2}<\frac{6}{7}$
$\frac{7}{8}×\frac{10}{11}=\frac{10}{11}÷\frac{8}{7}$
$\frac{3}{5}÷\frac{99}{100}>\frac{3}{5}$
$\frac{5}{9}÷\frac{3}{5}=\frac{5}{9}÷3×5$
$\frac{7}{8}×\frac{10}{11}=\frac{10}{11}÷\frac{8}{7}$
$\frac{3}{5}÷\frac{99}{100}>\frac{3}{5}$
$\frac{5}{9}÷\frac{3}{5}=\frac{5}{9}÷3×5$
4. 大、小两个正方体的表面积比是$4:1$,则它们的体积比是(
8:1
)。答案:8:1
解析:
设大正方体的棱长为$a$,小正方体的棱长为$b$。
正方体表面积公式为$6×棱长^{2}$,已知表面积比是$4:1$,则$\frac{6a^{2}}{6b^{2}}=\frac{4}{1}$,化简得$\frac{a^{2}}{b^{2}} = 4$,所以$\frac{a}{b}=2$。
正方体体积公式为$棱长^{3}$,体积比为$\frac{a^{3}}{b^{3}}=(\frac{a}{b})^{3}=2^{3}=8$,即体积比是$8:1$。
8:1
正方体表面积公式为$6×棱长^{2}$,已知表面积比是$4:1$,则$\frac{6a^{2}}{6b^{2}}=\frac{4}{1}$,化简得$\frac{a^{2}}{b^{2}} = 4$,所以$\frac{a}{b}=2$。
正方体体积公式为$棱长^{3}$,体积比为$\frac{a^{3}}{b^{3}}=(\frac{a}{b})^{3}=2^{3}=8$,即体积比是$8:1$。
8:1
5. 20吨煤,若每天烧去它的$\frac {1}{5}$,可以烧(
5
)天;若每天烧去$\frac {1}{5}$吨,可以烧(100
)天。答案:5 100
解析:
1. $1÷\frac{1}{5}=5$(天)
2. $20÷\frac{1}{5}=100$(天)
5 100
2. $20÷\frac{1}{5}=100$(天)
5 100
6. 水结成冰后,体积增加$\frac {1}{10}$。15升的水结成冰后,体积增加(
$\frac{3}{2}$
)升;(150
)立方分米的水结成冰后,体积会增加15升。答案:$\frac{3}{2}$ 150
解析:
15×$\frac{1}{10}$=$\frac{3}{2}$(升)
15÷$\frac{1}{10}$=150(立方分米)
$\frac{3}{2}$;150
15÷$\frac{1}{10}$=150(立方分米)
$\frac{3}{2}$;150
7. 做8人量的草莓冰激凌需要$\frac {1}{2}$升奶油、1千克草莓和250克糖。林晓做了够12个人吃的草莓冰激凌,她用了(
$\frac{3}{4}$
)升奶油;路然按同样的配比做草莓冰激凌,他用了$\frac {4}{5}$千克草莓,那么他用了(200
)克糖。答案:$\frac{3}{4}$ 200
解析:
12人是8人的$\frac{12}{8}=\frac{3}{2}$倍,奶油用量:$\frac{1}{2}×\frac{3}{2}=\frac{3}{4}$升;
草莓用量比等于人数比,$\frac{4}{5}$千克是1千克的$\frac{4}{5}$,糖用量:$250×\frac{4}{5}=200$克。
$\frac{3}{4}$ 200
草莓用量比等于人数比,$\frac{4}{5}$千克是1千克的$\frac{4}{5}$,糖用量:$250×\frac{4}{5}=200$克。
$\frac{3}{4}$ 200
8. 包馄饨,吴欢比吴双多包了$\frac {4}{5}$,吴双比吴欢少包8个,吴双包了(
10
)个。答案:10
解析:
设吴双包了$x$个馄饨,因为吴欢比吴双多包了$\frac{4}{5}$,所以吴欢包的馄饨数为$x + \frac{4}{5}x=\frac{9}{5}x$。
又因为吴双比吴欢少包8个,所以可列方程:$\frac{9}{5}x - x = 8$,即$\frac{4}{5}x = 8$,解得$x = 8÷\frac{4}{5}=8×\frac{5}{4}=10$。
10
又因为吴双比吴欢少包8个,所以可列方程:$\frac{9}{5}x - x = 8$,即$\frac{4}{5}x = 8$,解得$x = 8÷\frac{4}{5}=8×\frac{5}{4}=10$。
10
9. 一张长方形纸,长与宽的比是$5:3$,从这张纸上剪去一个最大的正方形,剩余纸的面积是$\frac {6}{5}$平方分米,原来长方形纸的面积是(
3
)平方分米。答案:3
解析:
设长方形的长为$5x$分米,宽为$3x$分米。
最大正方形的边长等于长方形的宽,即$3x$分米。
长方形面积为$5x × 3x = 15x^2$平方分米,正方形面积为$(3x)^2 = 9x^2$平方分米。
剩余面积为$15x^2 - 9x^2 = 6x^2$平方分米,已知剩余面积为$\frac{6}{5}$平方分米,所以$6x^2 = \frac{6}{5}$,解得$x^2 = \frac{1}{5}$。
原来长方形面积为$15x^2 = 15 × \frac{1}{5} = 3$平方分米。
3
最大正方形的边长等于长方形的宽,即$3x$分米。
长方形面积为$5x × 3x = 15x^2$平方分米,正方形面积为$(3x)^2 = 9x^2$平方分米。
剩余面积为$15x^2 - 9x^2 = 6x^2$平方分米,已知剩余面积为$\frac{6}{5}$平方分米,所以$6x^2 = \frac{6}{5}$,解得$x^2 = \frac{1}{5}$。
原来长方形面积为$15x^2 = 15 × \frac{1}{5} = 3$平方分米。
3
10. 有两张大小相同的长方形纸条按图①放置,现在将这两张长方形纸条分别向左、右方向平移至图②所示的位置,则每张长方形纸条的长是(
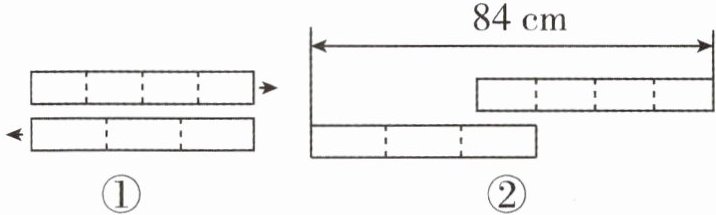
48
)厘米。
答案:48
11. 乐乐把自己绘本的$\frac {1}{5}$送给丁丁后,两人的绘本数正好相等,原来乐乐比丁丁多8本绘本,乐乐原来有(
20
)本绘本。答案:20
解析:
设乐乐原来有$x$本绘本,则乐乐送给丁丁$\frac{1}{5}x$本后,乐乐剩余$x - \frac{1}{5}x=\frac{4}{5}x$本。
因为此时两人绘本数相等,所以丁丁原来有$\frac{4}{5}x - \frac{1}{5}x=\frac{3}{5}x$本。
又因为原来乐乐比丁丁多8本,所以$x - \frac{3}{5}x = 8$,即$\frac{2}{5}x = 8$,解得$x = 8 ÷ \frac{2}{5}=8×\frac{5}{2}=20$。
20
因为此时两人绘本数相等,所以丁丁原来有$\frac{4}{5}x - \frac{1}{5}x=\frac{3}{5}x$本。
又因为原来乐乐比丁丁多8本,所以$x - \frac{3}{5}x = 8$,即$\frac{2}{5}x = 8$,解得$x = 8 ÷ \frac{2}{5}=8×\frac{5}{2}=20$。
20
12. 一批零件分给师徒两人完成,师傅完成了自己任务的$\frac {7}{12}$,徒弟完成了自己任务的$\frac {4}{9}$,这时他们剩下的零件数量一样多。师傅和徒弟分到的零件数量的最简单的整数比是(
4:3
)。答案:4:3
解析:
设师傅分到的零件数量为$x$,徒弟分到的零件数量为$y$。
师傅剩下的零件数量为$x - \frac{7}{12}x=\frac{5}{12}x$,徒弟剩下的零件数量为$y - \frac{4}{9}y=\frac{5}{9}y$。
由题意得$\frac{5}{12}x = \frac{5}{9}y$,两边同时除以$5$得$\frac{1}{12}x=\frac{1}{9}y$,则$x:y=\frac{1}{9}:\frac{1}{12}=4:3$。
4:3
师傅剩下的零件数量为$x - \frac{7}{12}x=\frac{5}{12}x$,徒弟剩下的零件数量为$y - \frac{4}{9}y=\frac{5}{9}y$。
由题意得$\frac{5}{12}x = \frac{5}{9}y$,两边同时除以$5$得$\frac{1}{12}x=\frac{1}{9}y$,则$x:y=\frac{1}{9}:\frac{1}{12}=4:3$。
4:3
13. 如图,有两个同心圆,它们的直径比是$2:3$,用线段分割成8块,相同的字母代表相同的面积,则$4A:B$的比值是(
$\frac{16}{3}$
)。答案:$\frac{16}{3}$
解析:
设小圆直径为$2d$,则大圆直径为$3d$,小圆半径$r = d$,大圆半径$R=\frac{3d}{2}$。
小圆面积$S_小=\pi r^2=\pi d^2$,大圆面积$S_大=\pi R^2=\pi (\frac{3d}{2})^2=\frac{9}{4}\pi d^2$。
圆环面积$S_环=S_大 - S_小=\frac{9}{4}\pi d^2-\pi d^2=\frac{5}{4}\pi d^2$。
由图知,小圆被分成3个$A$,则$3A = S_小=\pi d^2$,$A=\frac{\pi d^2}{3}$。
圆环被分成5个$B$,则$5B = S_环=\frac{5}{4}\pi d^2$,$B=\frac{\pi d^2}{4}$。
$4A:B=4×\frac{\pi d^2}{3}:\frac{\pi d^2}{4}=\frac{4}{3}:\frac{1}{4}=\frac{16}{3}$。
$\frac{16}{3}$
小圆面积$S_小=\pi r^2=\pi d^2$,大圆面积$S_大=\pi R^2=\pi (\frac{3d}{2})^2=\frac{9}{4}\pi d^2$。
圆环面积$S_环=S_大 - S_小=\frac{9}{4}\pi d^2-\pi d^2=\frac{5}{4}\pi d^2$。
由图知,小圆被分成3个$A$,则$3A = S_小=\pi d^2$,$A=\frac{\pi d^2}{3}$。
圆环被分成5个$B$,则$5B = S_环=\frac{5}{4}\pi d^2$,$B=\frac{\pi d^2}{4}$。
$4A:B=4×\frac{\pi d^2}{3}:\frac{\pi d^2}{4}=\frac{4}{3}:\frac{1}{4}=\frac{16}{3}$。
$\frac{16}{3}$
14. 妈妈买回橘子和苹果共60个,其中橘子占$\frac {2}{5}$,吃掉一些苹果后,苹果和橘子的个数比是$5:4$。吃掉了
6
个苹果。答案:6 提示:由题意可知,橘子有$60×\frac{2}{5}=24$(个),吃掉一些苹果的前后,橘子的个数不变,当苹果与橘子的个数比是5:4时,苹果有$24÷4×5=30$(个),吃了$60 - 24 - 30 = 6$(个)苹果。
解析:
橘子的个数:$60×\frac{2}{5}=24$(个)
苹果和橘子的个数比是$5:4$时,苹果的个数:$24÷4×5=30$(个)
原来苹果的个数:$60 - 24=36$(个)
吃掉苹果的个数:$36 - 30=6$(个)
6
苹果和橘子的个数比是$5:4$时,苹果的个数:$24÷4×5=30$(个)
原来苹果的个数:$60 - 24=36$(个)
吃掉苹果的个数:$36 - 30=6$(个)
6
15. 如图,已知三角形ABC的面积是60平方米,$BD:DC= 2:1$,$CE:EA= 3:1$,则三角形BDE的面积是(

30
)平方米。
答案:30 提示:根据$CE:EA = 3:1$可知,三角形BCE的面积占三角形ABC面积的$\frac{3}{3 + 1}$,由三角形ABC的面积可求出三角形BCE的面积;根据$BD:DC = 2:1$可知,三角形BDE的面积占三角形BCE面积的$\frac{2}{2 + 1}$,由三角形BCE的面积可求出三角形BDE的面积,则三角形BDE的面积为$60×\frac{3}{3 + 1}×\frac{2}{2 + 1}=30$(平方米)。
解析:
因为$CE:EA = 3:1$,所以三角形$BCE$的面积占三角形$ABC$面积的$\frac{3}{3 + 1}$。
三角形$ABC$的面积是$60$平方米,故三角形$BCE$的面积为$60×\frac{3}{4} = 45$平方米。
又因为$BD:DC = 2:1$,所以三角形$BDE$的面积占三角形$BCE$面积的$\frac{2}{2 + 1}$。
因此,三角形$BDE$的面积为$45×\frac{2}{3} = 30$平方米。
30
三角形$ABC$的面积是$60$平方米,故三角形$BCE$的面积为$60×\frac{3}{4} = 45$平方米。
又因为$BD:DC = 2:1$,所以三角形$BDE$的面积占三角形$BCE$面积的$\frac{2}{2 + 1}$。
因此,三角形$BDE$的面积为$45×\frac{2}{3} = 30$平方米。
30