1. $8:(
10
)= 4:5= \frac{(16
)}{20}= \frac{4+(20
)}{5×6}$答案:10 16 20
2. $\frac{7}{12}$分= (
7 立方米 20 立方分米= (
$\frac{7}{720}$
)时 $\frac{3}{50}$公顷= (600
)平方米7 立方米 20 立方分米= (
$7\frac{1}{50}$
)立方米答案:$\frac{7}{720}$ 600 $7\frac{1}{50}$
3. 在圆圈里填上“>”“<”或“=”。
$\frac{4}{3}×\frac{9}{10}$
$4÷\frac{4}{9}$
$\frac{4}{3}×\frac{9}{10}$
>
$\frac{9}{10}$ $\frac{10}{11}÷\frac{5}{6}$>
$\frac{10}{11}×\frac{5}{6}$$4÷\frac{4}{9}$
>
$\frac{4}{9}÷4$ $\frac{2}{7}×\frac{6}{13}$=
$\frac{6}{7}×\frac{2}{13}$答案:> > > =
解析:
$\frac{4}{3}×\frac{9}{10}>\frac{9}{10}$
$\frac{10}{11}÷\frac{5}{6}>\frac{10}{11}×\frac{5}{6}$
$4÷\frac{4}{9}>\frac{4}{9}÷4$
$\frac{2}{7}×\frac{6}{13}=\frac{6}{7}×\frac{2}{13}$
$\frac{10}{11}÷\frac{5}{6}>\frac{10}{11}×\frac{5}{6}$
$4÷\frac{4}{9}>\frac{4}{9}÷4$
$\frac{2}{7}×\frac{6}{13}=\frac{6}{7}×\frac{2}{13}$
4. 甲数的倒数是最小的质数,乙数的倒数是最小的合数,甲数与乙数最简单的整数比是(
2:1
)。答案:2:1
解析:
最小的质数是2,甲数的倒数是2,甲数是$\frac{1}{2}$。
最小的合数是4,乙数的倒数是4,乙数是$\frac{1}{4}$。
甲数与乙数的比是$\frac{1}{2}:\frac{1}{4}=(\frac{1}{2}×4):(\frac{1}{4}×4)=2:1$。
2:1
最小的合数是4,乙数的倒数是4,乙数是$\frac{1}{4}$。
甲数与乙数的比是$\frac{1}{2}:\frac{1}{4}=(\frac{1}{2}×4):(\frac{1}{4}×4)=2:1$。
2:1
5. 小明看一本故事书,3 天看了全书的$\frac{3}{5}$,照这样计算,剩下的还要看(
2
)天;如果第 4 天他从第 106 页开始看起,这本故事书一共有(175
)页。答案:2 175
解析:
1. 设全书为单位“1”,每天看的占比为$\frac{3}{5}÷3=\frac{1}{5}$,剩下全书的$1 - \frac{3}{5}=\frac{2}{5}$,还需天数$\frac{2}{5}÷\frac{1}{5}=2$天。
2. 前3天看的页数为$106 - 1 = 105$页,全书页数为$105÷\frac{3}{5}=175$页。
2 175
2. 前3天看的页数为$106 - 1 = 105$页,全书页数为$105÷\frac{3}{5}=175$页。
2 175
6. 找规律填空:$\frac{5}{4},\frac{1}{2},\frac{1}{5},\frac{2}{25}$,
$\frac{4}{125}$
,$\frac{8}{625}$
。答案:$\frac{4}{125}$ $\frac{8}{625}$
7. 两只相同的杯子中装满糖水,一只杯子中糖与水的比是 1:9,另一只杯子中糖与水的比是 1:11。若把两杯糖水全部倒入一只大杯子中,这时糖与水的比是(
11:109
)。答案:11:109
解析:
设每只杯子的容积为单位“1”。
第一只杯子中糖的量:$\frac{1}{1 + 9} = \frac{1}{10}$,水的量:$\frac{9}{1 + 9} = \frac{9}{10}$。
第二只杯子中糖的量:$\frac{1}{1 + 11} = \frac{1}{12}$,水的量:$\frac{11}{1 + 11} = \frac{11}{12}$。
混合后糖的总量:$\frac{1}{10} + \frac{1}{12} = \frac{6}{60} + \frac{5}{60} = \frac{11}{60}$。
混合后水的总量:$\frac{9}{10} + \frac{11}{12} = \frac{54}{60} + \frac{55}{60} = \frac{109}{60}$。
糖与水的比:$\frac{11}{60} : \frac{109}{60} = 11:109$。
11:109
第一只杯子中糖的量:$\frac{1}{1 + 9} = \frac{1}{10}$,水的量:$\frac{9}{1 + 9} = \frac{9}{10}$。
第二只杯子中糖的量:$\frac{1}{1 + 11} = \frac{1}{12}$,水的量:$\frac{11}{1 + 11} = \frac{11}{12}$。
混合后糖的总量:$\frac{1}{10} + \frac{1}{12} = \frac{6}{60} + \frac{5}{60} = \frac{11}{60}$。
混合后水的总量:$\frac{9}{10} + \frac{11}{12} = \frac{54}{60} + \frac{55}{60} = \frac{109}{60}$。
糖与水的比:$\frac{11}{60} : \frac{109}{60} = 11:109$。
11:109
8. 一块长方形菜地,宽比长短$\frac{3}{8}$,如果宽增加 12 米,那么变成正方形菜地。这块长方形菜地的面积是(
640
)平方米。答案:640
解析:
设长方形菜地的长为$x$米,宽比长短$\frac{3}{8}$,则宽为$x - \frac{3}{8}x=\frac{5}{8}x$米。
宽增加12米变成正方形,此时宽等于长,可得方程:$\frac{5}{8}x + 12 = x$
解方程:$x - \frac{5}{8}x=12$,$\frac{3}{8}x=12$,$x=12×\frac{8}{3}=32$
宽为$\frac{5}{8}×32 = 20$米
面积为$32×20 = 640$平方米
640
宽增加12米变成正方形,此时宽等于长,可得方程:$\frac{5}{8}x + 12 = x$
解方程:$x - \frac{5}{8}x=12$,$\frac{3}{8}x=12$,$x=12×\frac{8}{3}=32$
宽为$\frac{5}{8}×32 = 20$米
面积为$32×20 = 640$平方米
640
9. 一个正方体木块,沿着同一方向,把它切成 4 个完全相同的小长方体后,表面积增加了 120 平方厘米,则这个正方体木块原来的表面积是(
120
)平方厘米。答案:120
解析:
切成4个小长方体,需要切3次,每切1次增加2个正方形面,共增加$3×2 = 6$个面。
每个面的面积为$120÷6 = 20$平方厘米。
正方体有6个面,原来的表面积是$20×6 = 120$平方厘米。
120
每个面的面积为$120÷6 = 20$平方厘米。
正方体有6个面,原来的表面积是$20×6 = 120$平方厘米。
120
10. 甲、乙两个仓库中各存有一些粮食,甲仓库比乙仓库多存 200 吨,从两个仓库中各运走 50 吨后,甲仓库比乙仓库多$\frac{4}{5}$,乙仓库原来存粮(
300
)吨。答案:300
解析:
设乙仓库原来存粮$x$吨,则甲仓库原来存粮$(x + 200)$吨。
运走50吨后,乙仓库有$(x - 50)$吨,甲仓库有$(x + 200 - 50) = (x + 150)$吨。
根据题意可得:$x + 150 = (x - 50) + \frac{4}{5}(x - 50)$
化简得:$x + 150 = \frac{9}{5}(x - 50)$
两边同乘5:$5x + 750 = 9(x - 50)$
展开:$5x + 750 = 9x - 450$
移项:$9x - 5x = 750 + 450$
计算:$4x = 1200$
解得:$x = 300$
300
运走50吨后,乙仓库有$(x - 50)$吨,甲仓库有$(x + 200 - 50) = (x + 150)$吨。
根据题意可得:$x + 150 = (x - 50) + \frac{4}{5}(x - 50)$
化简得:$x + 150 = \frac{9}{5}(x - 50)$
两边同乘5:$5x + 750 = 9(x - 50)$
展开:$5x + 750 = 9x - 450$
移项:$9x - 5x = 750 + 450$
计算:$4x = 1200$
解得:$x = 300$
300
11. 张叔叔用 144 米长的篱笆靠墙(墙足够长)围了一个长方形花圃,如图,已知长方形花圃的长与宽的比是 2:1。这个花圃的面积是(
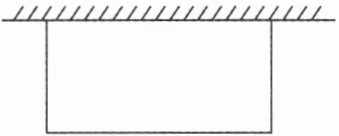
2592
)平方米。
答案:2592
解析:
设长方形花圃的宽为$x$米,长为$2x$米。
由图可知,篱笆靠墙围成的长方形,篱笆只围了一个长和两个宽,所以$2x + 2x = 144$
$4x = 144$
$x = 36$
长:$2x = 2×36 = 72$(米)
面积:$72×36 = 2592$(平方米)
2592
由图可知,篱笆靠墙围成的长方形,篱笆只围了一个长和两个宽,所以$2x + 2x = 144$
$4x = 144$
$x = 36$
长:$2x = 2×36 = 72$(米)
面积:$72×36 = 2592$(平方米)
2592
12. 一个无盖容器如图所示(单位:分米),如果用铁皮做一个这样的容器,竖直放置,至少需要铁皮(

23
)平方分米,能容水(6
)升。
答案:23 6
解析:
至少需要铁皮
容器表面积=底面积+侧面积
底面积:$2 × 1 = 2$(平方分米)
侧面积:
$1 × 4 + 1 × 3 + (3+4)×2÷2×2$
$=4 + 3 + 14$
$=21$(平方分米)
总表面积:$2 + 21 = 23$(平方分米)
能容水体积
体积=长×宽×高(以最小高度3分米计算)
$2 × 1 × 3 = 6$(立方分米)=6升
23 6
容器表面积=底面积+侧面积
底面积:$2 × 1 = 2$(平方分米)
侧面积:
$1 × 4 + 1 × 3 + (3+4)×2÷2×2$
$=4 + 3 + 14$
$=21$(平方分米)
总表面积:$2 + 21 = 23$(平方分米)
能容水体积
体积=长×宽×高(以最小高度3分米计算)
$2 × 1 × 3 = 6$(立方分米)=6升
23 6
13. 小明将一块橡皮泥捏成如图的形状,长方体甲 A 面的面积是 15 平方厘米,长方体乙 B 面的面积是 10 平方厘米,A 面的高度比 B 面高 3 厘米,现将甲长方体的一部分橡皮泥补捏到乙长方体上,使得两长方体一样高,则 A 面的高度将下降(

1.2
)厘米。
答案:1.2 提示:变动的过程实际上是把底面积是15平方厘米的甲长方体高出部分变成底面积是15 + 10 = 25(平方厘米)的长方体。求出甲长方体高出部分变动后的高度,再用3厘米减去这个高度就是A面下降的高度。
解析:
设变动后两长方体的高度为$h$厘米,A面原来的高度为$h + x$厘米,B面原来的高度为$h - (3 - x)$厘米(其中$x$为A面下降的高度)。
甲高出部分的体积为$15x$,这部分体积补到乙后,乙增加的体积为$10(3 - x)$。
因为体积相等,所以$15x = 10(3 - x)$,
$15x = 30 - 10x$,
$25x = 30$,
$x = \frac{30}{25} = 1.2$。
1.2
甲高出部分的体积为$15x$,这部分体积补到乙后,乙增加的体积为$10(3 - x)$。
因为体积相等,所以$15x = 10(3 - x)$,
$15x = 30 - 10x$,
$25x = 30$,
$x = \frac{30}{25} = 1.2$。
1.2
14. 如图,三角形 ABC 的面积是 480 平方厘米,已知三角形 ABD 的面积是三角形 ABC 面积的$\frac{3}{4}$,且 AE= EF= FD,则三角形 ABE 的面积是(
120
)平方厘米。答案:120 提示:由AE = EF = FD,可知三角形ABE的面积是三角形ABD面积的$\frac{1}{3}$,而三角形ABD的面积又是三角形ABC面积的$\frac{3}{4}$,所以三角形ABE的面积是$480×\frac{3}{4}×\frac{1}{3}=120$(平方厘米)。
解析:
三角形ABD的面积为$480×\frac{3}{4} = 360$平方厘米。因为AE=EF=FD,所以三角形ABE、三角形BEF、三角形BFD的面积相等,即三角形ABE的面积是三角形ABD面积的$\frac{1}{3}$。则三角形ABE的面积为$360×\frac{1}{3}=120$平方厘米。
120
120