1. 下面可以用 2:3 表示的有(
情境① 白球与蓝球的个数比
情境② 钢笔与铅笔的长度比
情境③ 水与糖水的质量比
情境④ 甲与乙的体积比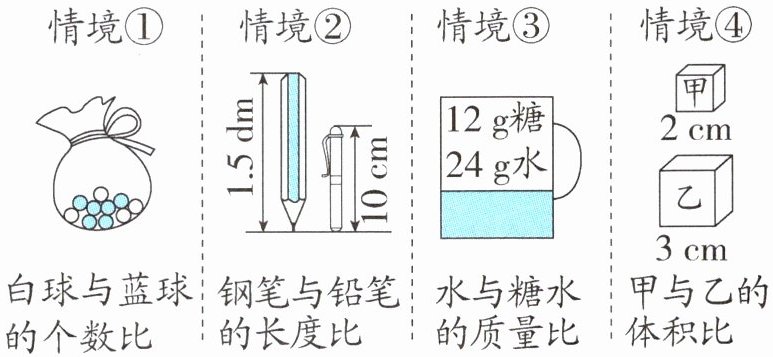
A.1
B.2
C.3
D.4
C
)个。情境① 白球与蓝球的个数比
情境② 钢笔与铅笔的长度比
情境③ 水与糖水的质量比
情境④ 甲与乙的体积比

A.1
B.2
C.3
D.4
答案:C
解析:
情境①:白球6个,蓝球9个,$6:9=2:3$;
情境②:钢笔10cm,铅笔1.5dm=15cm,$10:15=2:3$;
情境③:水24g,糖水$12+24=36$g,$24:36=2:3$;
情境④:甲棱长2cm,体积$2^3=8$cm³;乙棱长3cm,体积$3^3=27$cm³,$8:27≠2:3$;
共3个可用$2:3$表示。
C
情境②:钢笔10cm,铅笔1.5dm=15cm,$10:15=2:3$;
情境③:水24g,糖水$12+24=36$g,$24:36=2:3$;
情境④:甲棱长2cm,体积$2^3=8$cm³;乙棱长3cm,体积$3^3=27$cm³,$8:27≠2:3$;
共3个可用$2:3$表示。
C
2. 轩轩 4 分钟步行$\frac{3}{10}$千米,他用这样的速度在长$\frac{2}{5}$千米的跑道上走一圈,要用几分钟?下列算式中,正确的有(
$\frac{3}{10}÷4×\frac{2}{5}$ $4÷\frac{3}{10}×\frac{2}{5}$ $\frac{2}{5}÷\frac{3}{10}×4$ $\frac{2}{5}÷(\frac{3}{10}÷4)$
A.1
B.2
C.3
D.4
C
)个。$\frac{3}{10}÷4×\frac{2}{5}$ $4÷\frac{3}{10}×\frac{2}{5}$ $\frac{2}{5}÷\frac{3}{10}×4$ $\frac{2}{5}÷(\frac{3}{10}÷4)$
A.1
B.2
C.3
D.4
答案:C
解析:
轩轩的步行速度为:$\frac{3}{10}÷4$(千米/分钟)
走$\frac{2}{5}$千米所需时间为:$\frac{2}{5}÷(\frac{3}{10}÷4)$,此算式正确。
另一种思路:4分钟走$\frac{3}{10}$千米,则走1千米需要$4÷\frac{3}{10}$分钟,走$\frac{2}{5}$千米需要$4÷\frac{3}{10}×\frac{2}{5}$分钟,此算式正确。
还可理解为:$\frac{2}{5}$千米是$\frac{3}{10}$千米的$\frac{2}{5}÷\frac{3}{10}$倍,所以时间也是4分钟的$\frac{2}{5}÷\frac{3}{10}$倍,即$\frac{2}{5}÷\frac{3}{10}×4$分钟,此算式正确。
$\frac{3}{10}÷4×\frac{2}{5}$表示的是路程,不是时间,错误。
正确的算式有3个。
C
走$\frac{2}{5}$千米所需时间为:$\frac{2}{5}÷(\frac{3}{10}÷4)$,此算式正确。
另一种思路:4分钟走$\frac{3}{10}$千米,则走1千米需要$4÷\frac{3}{10}$分钟,走$\frac{2}{5}$千米需要$4÷\frac{3}{10}×\frac{2}{5}$分钟,此算式正确。
还可理解为:$\frac{2}{5}$千米是$\frac{3}{10}$千米的$\frac{2}{5}÷\frac{3}{10}$倍,所以时间也是4分钟的$\frac{2}{5}÷\frac{3}{10}$倍,即$\frac{2}{5}÷\frac{3}{10}×4$分钟,此算式正确。
$\frac{3}{10}÷4×\frac{2}{5}$表示的是路程,不是时间,错误。
正确的算式有3个。
C
3. 下列算式的结果与数 p 最接近的是(

A.$m + n$
B.$m×n$
C.$m÷n$
D.$n÷m$
D
)。
A.$m + n$
B.$m×n$
C.$m÷n$
D.$n÷m$
答案:D
解析:
设 $ m = \frac{1}{3} $, $ n = \frac{2}{3} $, $ p = 2.5 $
$ m + n = \frac{1}{3} + \frac{2}{3} = 1 $
$ m×n = \frac{1}{3}×\frac{2}{3} = \frac{2}{9} \approx 0.22 $
$ m÷n = \frac{1}{3}÷\frac{2}{3} = \frac{1}{2} = 0.5 $
$ n÷m = \frac{2}{3}÷\frac{1}{3} = 2 $
D
$ m + n = \frac{1}{3} + \frac{2}{3} = 1 $
$ m×n = \frac{1}{3}×\frac{2}{3} = \frac{2}{9} \approx 0.22 $
$ m÷n = \frac{1}{3}÷\frac{2}{3} = \frac{1}{2} = 0.5 $
$ n÷m = \frac{2}{3}÷\frac{1}{3} = 2 $
D
4. 下列说法中,不正确的有(
① 两个真分数相乘的积一定小于它们相除的商。
② 一个长方体相邻的 2 个面是正方形,这个长方体一定是正方体。
③ 1 米长的绳子,剪下它的$\frac{1}{4}$后,又接上$\frac{1}{4}$米,这时绳长不变。
④ 从 A 地到 B 地,甲车需 6 小时,乙车需 4 小时,甲乙两车的平均速度之比是 3:2。
A.1
B.2
C.3
D.4
A
)个。① 两个真分数相乘的积一定小于它们相除的商。
② 一个长方体相邻的 2 个面是正方形,这个长方体一定是正方体。
③ 1 米长的绳子,剪下它的$\frac{1}{4}$后,又接上$\frac{1}{4}$米,这时绳长不变。
④ 从 A 地到 B 地,甲车需 6 小时,乙车需 4 小时,甲乙两车的平均速度之比是 3:2。
A.1
B.2
C.3
D.4
答案:A
解析:
①设真分数为$\frac{a}{b}$、$\frac{c}{d}$($a < b$,$c < d$,$a,b,c,d$为正整数),积为$\frac{ac}{bd}$,商为$\frac{ad}{bc}$。因$ac < ad$($c < d$),$bd > bc$($d > c$),则$\frac{ac}{bd} < \frac{ad}{bc}$,正确。
②长方体相邻两面为正方形,则长=宽=高,是正方体,正确。
③原长1米,剪下$\frac{1}{4}$后剩$1 - 1×\frac{1}{4} = \frac{3}{4}$米,接上$\frac{1}{4}$米后为$\frac{3}{4} + \frac{1}{4} = 1$米,绳长不变,正确。
④设路程为1,甲车速度$\frac{1}{6}$,乙车速度$\frac{1}{4}$,速度比$\frac{1}{6}:\frac{1}{4} = 2:3$,原说法错误。
不正确的有1个。
A
②长方体相邻两面为正方形,则长=宽=高,是正方体,正确。
③原长1米,剪下$\frac{1}{4}$后剩$1 - 1×\frac{1}{4} = \frac{3}{4}$米,接上$\frac{1}{4}$米后为$\frac{3}{4} + \frac{1}{4} = 1$米,绳长不变,正确。
④设路程为1,甲车速度$\frac{1}{6}$,乙车速度$\frac{1}{4}$,速度比$\frac{1}{6}:\frac{1}{4} = 2:3$,原说法错误。
不正确的有1个。
A
5. 冰融化成水后,水的体积是冰的$\frac{9}{10}$,将一块体积为 3600 立方厘米的长方体冰块放在一个底面积为 600 平方厘米的空的长方体容器中,当冰完全融化后,容器中的水深(
A.6.8
B.6.3
C.6
D.5.4
D
)厘米。A.6.8
B.6.3
C.6
D.5.4
答案:D
解析:
水的体积:$3600×\frac{9}{10} = 3240$(立方厘米)
水深:$3240÷600 = 5.4$(厘米)
D
水深:$3240÷600 = 5.4$(厘米)
D
6. 在由小正方体组成的长方体中,拿走两小块,如图,在表面涂上红漆,三面都涂色的小正方体有( )个。

A.8
B.9
C.10
D.11

A.8
B.9
C.10
D.11
答案:
D 提示:如图,除了顶点处的8个小正方体,还有3个小正方体也是三面涂色,共有11个。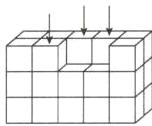
D 提示:如图,除了顶点处的8个小正方体,还有3个小正方体也是三面涂色,共有11个。

7. 在右图中添一个小正方形,使它成为一个正方体的展开图,添加的方法共有( )。

A.2 种
B.3 种
C.4 种
D.5 种

A.2 种
B.3 种
C.4 种
D.5 种
答案:
C 提示:四种添加方法分别如图。
C 提示:四种添加方法分别如图。

8. 将两个石块分别放入两个完全相同的长方体玻璃缸中,甲缸中的水面上升 10 厘米,乙缸中的水面上升 7 厘米。甲、乙两个玻璃缸中石块的体积比是(
A.10:7
B.7:10
C.100:49
D.10:3
10:7
)。(水未溢出,且石块完全没入水中)A.10:7
B.7:10
C.100:49
D.10:3
答案:A 提示:上升的水的体积就是放入水中石块的体积。
1. 直接写出得数。
$\frac{1}{2}÷\frac{5}{8}=$
$\frac{5}{7}×\frac{4}{15}=$
$\frac{1}{2}÷\frac{5}{8}=$
$\frac{4}{5}$
$\frac{2}{3}×36=$24
$\frac{11}{18}÷\frac{11}{12}=$$\frac{2}{3}$
$\frac{5}{7}×\frac{4}{15}=$
$\frac{4}{21}$
$\frac{3}{5}÷\frac{5}{3}=$$\frac{9}{25}$
$\frac{1}{5}×6÷\frac{1}{5}×6=$36
答案:$\frac{4}{5}$ 24 $\frac{2}{3}$ $\frac{4}{21}$ $\frac{9}{25}$ 36
2. 计算下面各题。
$\frac{3}{8}×\frac{6}{13}÷\frac{9}{26}$ $\frac{1}{6}÷\frac{5}{18}÷27$ $\frac{4}{21}÷\frac{5}{16}×\frac{7}{24}$
$\frac{3}{8}×\frac{6}{13}÷\frac{9}{26}$ $\frac{1}{6}÷\frac{5}{18}÷27$ $\frac{4}{21}÷\frac{5}{16}×\frac{7}{24}$
答案:$\frac{3}{8}×\frac{6}{13}÷\frac{9}{26}=\frac{1}{2}$ $\frac{1}{6}÷\frac{5}{18}÷27=\frac{1}{45}$ $\frac{4}{21}÷\frac{5}{16}×\frac{7}{24}=\frac{8}{45}$
解析:
$\frac{3}{8}×\frac{6}{13}÷\frac{9}{26}$
$=\frac{3}{8}×\frac{6}{13}×\frac{26}{9}$
$=\frac{3×6×26}{8×13×9}$
$=\frac{3×6×2×13}{8×13×9}$
$=\frac{3×6×2}{8×9}$
$=\frac{36}{72}$
$=\frac{1}{2}$
$\frac{1}{6}÷\frac{5}{18}÷27$
$=\frac{1}{6}×\frac{18}{5}×\frac{1}{27}$
$=\frac{1×18×1}{6×5×27}$
$=\frac{18}{810}$
$=\frac{1}{45}$
$\frac{4}{21}÷\frac{5}{16}×\frac{7}{24}$
$=\frac{4}{21}×\frac{16}{5}×\frac{7}{24}$
$=\frac{4×16×7}{21×5×24}$
$=\frac{4×16×7}{3×7×5×24}$
$=\frac{4×16}{3×5×24}$
$=\frac{64}{360}$
$=\frac{8}{45}$
$=\frac{3}{8}×\frac{6}{13}×\frac{26}{9}$
$=\frac{3×6×26}{8×13×9}$
$=\frac{3×6×2×13}{8×13×9}$
$=\frac{3×6×2}{8×9}$
$=\frac{36}{72}$
$=\frac{1}{2}$
$\frac{1}{6}÷\frac{5}{18}÷27$
$=\frac{1}{6}×\frac{18}{5}×\frac{1}{27}$
$=\frac{1×18×1}{6×5×27}$
$=\frac{18}{810}$
$=\frac{1}{45}$
$\frac{4}{21}÷\frac{5}{16}×\frac{7}{24}$
$=\frac{4}{21}×\frac{16}{5}×\frac{7}{24}$
$=\frac{4×16×7}{21×5×24}$
$=\frac{4×16×7}{3×7×5×24}$
$=\frac{4×16}{3×5×24}$
$=\frac{64}{360}$
$=\frac{8}{45}$
1. 涂一涂:在下图中用涂色部分表示$\frac{3}{7}$公顷。


答案:
 (涂法合理即可)
(涂法合理即可)
 (涂法合理即可)
(涂法合理即可)