4. (1) 一个分数分别与它本身相加、相减、相除, 所得的和、差、商相加得$\frac {5}{2}$, 这个分数是(
(2) 有一满杯水溶有 40 克奶粉, 搅匀后喝去$\frac {3}{5}$；然后加入 20 克奶粉, 加满水搅匀, 再喝去$\frac {3}{5}$；再加入 20 克奶粉, 再加满水搅匀, 仍喝去$\frac {3}{5}$。此时杯中剩下的奶粉有(
$\frac{3}{4}$
)。(2) 有一满杯水溶有 40 克奶粉, 搅匀后喝去$\frac {3}{5}$；然后加入 20 克奶粉, 加满水搅匀, 再喝去$\frac {3}{5}$；再加入 20 克奶粉, 再加满水搅匀, 仍喝去$\frac {3}{5}$。此时杯中剩下的奶粉有(
13.76
)克。答案：
(1)$\frac{3}{4}$ 提示:设这个分数为$x$，则相加为$2x$，相减为$0$，相除为$1$，可列方程为$2x + 1=\frac{5}{2}$，解得$x=\frac{3}{4}$。
(2)13.76 提示:本题中，奶粉的总量处在不断的变化中，也就是说，单位“1”是不固定的，但这种变化是有规律的，我们只要抓住这个规律，就能很巧妙地解决这道题。只要弄清楚所求数量占单位“1”的几分之几，再根据公式单位“1”×对应分率=对应数量求解即可。第一次喝去$\frac{3}{5}$后，所剩奶粉的质量为$40×(1 - \frac{3}{5})=16$(克)；第二次喝去$\frac{3}{5}$后，所剩奶粉的质量为$(16 + 20)×(1 - \frac{3}{5})=14.4$(克)；第三次喝去$\frac{3}{5}$后，所剩奶粉的质量为$(14.4 + 20)×(1 - \frac{3}{5})=13.76$(克)。
(1)$\frac{3}{4}$ 提示:设这个分数为$x$，则相加为$2x$，相减为$0$，相除为$1$，可列方程为$2x + 1=\frac{5}{2}$，解得$x=\frac{3}{4}$。
(2)13.76 提示:本题中，奶粉的总量处在不断的变化中，也就是说，单位“1”是不固定的，但这种变化是有规律的，我们只要抓住这个规律，就能很巧妙地解决这道题。只要弄清楚所求数量占单位“1”的几分之几，再根据公式单位“1”×对应分率=对应数量求解即可。第一次喝去$\frac{3}{5}$后，所剩奶粉的质量为$40×(1 - \frac{3}{5})=16$(克)；第二次喝去$\frac{3}{5}$后，所剩奶粉的质量为$(16 + 20)×(1 - \frac{3}{5})=14.4$(克)；第三次喝去$\frac{3}{5}$后，所剩奶粉的质量为$(14.4 + 20)×(1 - \frac{3}{5})=13.76$(克)。
5. 丢番图的墓志铭中写道: “童年占六分之一, 又过十二分之一, 两颊长胡, 再过七分之一, 点起结婚的蜡烛, 五年之后天赐贵子, 可怜迟到的宁馨儿, 享年仅及其父之半, 便进入冰冷的墓。悲伤只能用数论研究去弥补, 又过四年, 他也走完了人生的旅途。”你能计算出丢番图的寿命吗?
答案：
$(5 + 4)÷(1 - \frac{1}{6}-\frac{1}{12}-\frac{1}{7}-\frac{1}{2})=84$(岁) 提示:题中的数量关系可用下图表示: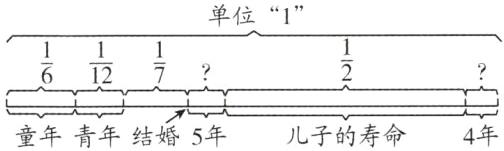
把丢番图的寿命看作单位“1”，根据5年之后生子，儿子比他早4年去世可知，$(5 + 4)$年相当于他的寿命的$(1 - \frac{1}{6}-\frac{1}{12}-\frac{1}{7}-\frac{1}{2})$。
$(5 + 4)÷(1 - \frac{1}{6}-\frac{1}{12}-\frac{1}{7}-\frac{1}{2})=84$(岁) 提示:题中的数量关系可用下图表示:
把丢番图的寿命看作单位“1”，根据5年之后生子，儿子比他早4年去世可知，$(5 + 4)$年相当于他的寿命的$(1 - \frac{1}{6}-\frac{1}{12}-\frac{1}{7}-\frac{1}{2})$。6. 有一个分数, 分子加 5 后可化简为$\frac {2}{3}$, 分子减 5 后可化简为$\frac {7}{18}$, 求这个分数。
答案：
$(\frac{2}{3}+\frac{7}{18})÷2=\frac{19}{36}$ 提示: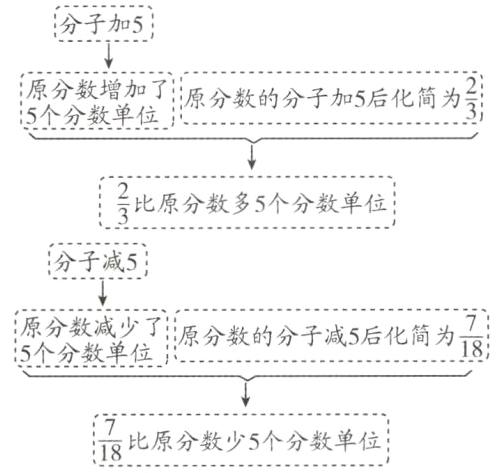
由此可以得出:$\frac{2}{3}$与$\frac{7}{18}$的和正好是原分数的2倍(多的5个分数单位和少的5个分数单位相互抵消)，用它们的和除以2就可以求出原分数。
$(\frac{2}{3}+\frac{7}{18})÷2=\frac{19}{36}$ 提示:
由此可以得出:$\frac{2}{3}$与$\frac{7}{18}$的和正好是原分数的2倍(多的5个分数单位和少的5个分数单位相互抵消)，用它们的和除以2就可以求出原分数。7. 运动会团体操训练组从甲、乙两个学校共挑选了 95 名队员。甲校队员中有$\frac {2}{9}$是男生, 乙校队员中有$\frac {13}{16}$是女生。甲、乙两校共有多少名男生参加团体操训练?
答案：$9×7 + 16×2 = 95$(人) 甲校:$9×7 = 63$(人) 乙校:$16×2 = 32$(人) $63×\frac{2}{9}+32×(1 - \frac{13}{16})=20$(人) 提示:甲校队员人数是9的倍数，乙校队员人数是16的倍数，即$9m + 16n = 95$，尝试推算$m = 7$，$n = 2$，即甲校参加的学生有$9×7 = 63$(人)，乙校参加的学生有$16×2 = 32$(人)。甲、乙两校参加训练的男生一共有$63×\frac{2}{9}+32×(1 - \frac{13}{16})=20$(人)。
解析：
甲校队员人数是9的倍数，乙校队员人数是16的倍数，设甲校有$9m$人，乙校有$16n$人，可得$9m + 16n = 95$。尝试推算得$m = 7$，$n = 2$，则甲校有$9×7 = 63$人，乙校有$16×2 = 32$人。
甲校男生人数：$63×\frac{2}{9} = 14$人。
乙校男生人数：$32×(1 - \frac{13}{16}) = 32×\frac{3}{16} = 6$人。
两校共有的男生人数：$14 + 6 = 20$人。
20
甲校男生人数：$63×\frac{2}{9} = 14$人。
乙校男生人数：$32×(1 - \frac{13}{16}) = 32×\frac{3}{16} = 6$人。
两校共有的男生人数：$14 + 6 = 20$人。
20
8. 模型意识 饲养场有黄牛和奶牛共 66 头, 奶牛的$\frac {1}{3}比黄牛的\frac {1}{6}$多 4 头, 黄牛和奶牛各有多少头?
答案：黄牛:$(66×\frac{1}{3}-4)÷(\frac{1}{6}+\frac{1}{3})=36$(头) 奶牛:$66 - 36 = 30$(头) 提示:奶牛的$\frac{1}{3}$和黄牛的$\frac{1}{3}$共有$66×\frac{1}{3}=22$(头)，黄牛的$(\frac{1}{6}+\frac{1}{3})$有$22 - 4 = 18$(头)，黄牛有$18÷(\frac{1}{6}+\frac{1}{3})=36$(头)，奶牛有$66 - 36 = 30$(头)。
解析：
黄牛：$(66×\frac{1}{3}-4)÷(\frac{1}{6}+\frac{1}{3})=36$（头）
奶牛：$66 - 36 = 30$（头）
奶牛：$66 - 36 = 30$（头）
9. 有两堆棋子, A 堆有白子 500 个和黑子 350 个, B 堆有白子 100 个和黑子 400 个, 为了使 A 堆中黑子占$\frac {1}{2}$, B 堆中黑子占$\frac {3}{4}$, 从 B 堆中拿到 A 堆的黑、白子各为多少个?
答案：$(500 + 350 + 100 + 400)×\frac{1}{2}=675$(个) $(400 + 350 - 675)÷(\frac{3}{4}-\frac{1}{2})=300$(个) $400 - 300×\frac{3}{4}=175$(个) $100 - 300×(1 - \frac{3}{4})=25$(个) 提示:假设每堆棋子中黑子都占$\frac{1}{2}$，那么黑子共有$(500 + 350 + 100 + 400)×\frac{1}{2}=675$(个)，后来B堆棋子有$(400 + 350 - 675)÷(\frac{3}{4}-\frac{1}{2})=300$(个)，则要从B堆拿到A堆的黑子个数为$400 - 300×\frac{3}{4}=175$(个)，要从B堆拿到A堆的白子个数为$100 - 300×(1 - \frac{3}{4})=25$(个)。
解析：
棋子总个数：$500 + 350 + 100 + 400 = 1350$（个）
假设每堆黑子都占$\frac{1}{2}$时黑子总数：$1350×\frac{1}{2}=675$（个）
实际黑子总数：$350 + 400 = 750$（个）
B堆棋子数：$(750 - 675)÷(\frac{3}{4}-\frac{1}{2})=300$（个）
从B堆拿到A堆的黑子数：$400 - 300×\frac{3}{4}=175$（个）
从B堆拿到A堆的白子数：$100 - 300×(1 - \frac{3}{4})=25$（个）
答：从B堆中拿到A堆的黑子175个，白子25个。
假设每堆黑子都占$\frac{1}{2}$时黑子总数：$1350×\frac{1}{2}=675$（个）
实际黑子总数：$350 + 400 = 750$（个）
B堆棋子数：$(750 - 675)÷(\frac{3}{4}-\frac{1}{2})=300$（个）
从B堆拿到A堆的黑子数：$400 - 300×\frac{3}{4}=175$（个）
从B堆拿到A堆的白子数：$100 - 300×(1 - \frac{3}{4})=25$（个）
答：从B堆中拿到A堆的黑子175个，白子25个。